Doges on Trial Part 3 - Cryptoeconomics Finale Edition

In the first two articles of this series, we saw some broad trends in juror voting patterns and then we took a closer look at cases in which attackers attempted to bribe jurors. In this article, we will consider a number of other interesting questions and observations that have arisen regarding the behavior of jurors in the Doges on Trial pilot.    

The “lazy strategy” of always voting for the most common response  

In the first article in our series, we saw that roughly 70% of all votes cast were for “not doge.” Then, one might naturally ask if it is/would have been profitable to set up a bot that deposits PNK and just votes “not doge” whenever it is drawn.

As a rough heuristic, imagine that we give such an attacker one vote in each case but, for simplicity, all of the existing votes still count and the outcomes of the cases are assumed not to change (after all, if this attacker had resulted in unjust outcomes, those could have been appealed). Then, if we denote by Ni and Di the number of “not doge” and “doge” votes in the ith case respectively, and if d is the deposit lost by incoherent jurors, the attacker's net returns are given by:

Based on the observed values of Di and Ni for each case (up through the cutoff to qualify for a payout of Dogecoins at disputeID 148), we compute that S=-48.9d, namely that such a strategy would have lost 48.9 more deposits than the PNK that it gained back. (Always voting “doge” is even worse; the equivalent calculation gives S=-78.3d.) This strategy essentially does not work as an attacker does not gain anything when she votes with a unanimous decision, and we have seen that most of the cases were, in fact, unanimous.

A more complete answer to this question would depend on what percentage of the total PNK deposited the attacker controlled; then we could consider the attacker's chance of being drawn in the ith case and calculate her expected return. However, we can perform a slightly more nuanced heuristic that takes into account the fact that an attacker would have more votes in appeals, when there are more total votes to be had, and that these cases are those that are most likely to profit the attacker as they tend to be contentious. To this end, we can weigh the cases by their total number of votes to compute:

Note, by not adjusting the Ni+1 denominator to reflect the attacker's greater number of votes, we actually overestimate the effect of these returns relative to the losses due to when the attacker is incoherent. Here it turns out that S'=-101.3d (and the value for the strategy of always voting “doge” is S'=-645.1d), so this strategy is still losing under this heuristic.

Evidence and Venetian Doges

A doge is, of course, a beloved meme image of a Shiba Inu. However, long before the creation of this meme, the word Doge was used to refer to the chief magistrate of the Republic of Venice. When we ask jurors "Does this image show a Doge?", they might reasonably rule that a portrait of Doge Leonardo Loredan of Venice:

belongs on the list. However, at the same time, a juror that knows the history of Venice might not expect her fellow jurors to also know that Venice was once ruled by Doges. So she might vote "not doge" in an attempt to be coherent even if she believes that the honest response is "doge".

This phenomenon underlies the importance of having a well-argued case presented to jurors, so that they have enough information to make an informed ruling. We expect, in general, that the kinds of evidence parties provide on their behalf will have an important influence on how jurors rule. For the Doge pilot, we didn't give submitters or challengers an explicit mechanism in which to present evidence to the jurors; however, submitters could embed text in their images, such as in the subsequent submission:  

On the other hand, the following, similar submission received somewhat more mixed results despite providing jurors with enough of a lead so that they could make an informed choice:

Perhaps, the fact that Paolo Lucio Anafesto had worse results than Leonardo Loredan may have something to do with the historical uncertainty over whether there ever really was a Doge Anafesto, an ambiguity that was expressed to jurors with the phrase "Believed to be." Indeed, the first historical records attesting to Anafesto's existence only date from the 11th century.  

Nonetheless, providing jurors with relevant evidence so far seems to improve their ability to collectively gravitate to well-informed choices. We expect to further investigate the effect and role of evidence in the future.

Images with both dogs and cats

Cases where images show both doges and cats have been notably controversial. In the payout policy for rewards for placing a cat image on the list, Kleros has specifically indicated that images that also contain a doge are not eligible for the reward.

However, the subcourt policy only asks if the images contain a doge.

There seems to be a tendency over time towards ruling these images as "not doge." Indeed, we identified 11 images that contained both a Shiba Inu and a cat. All 11 of these images were challenged; two of them managed to make it into the list in early August while the other nine have been rejected. A total of 72 votes were cast by jurors on these cases.

Performing a logistic regression that predicts the probability of a juror voting "doge" on such an image as a function of the date of last activity for that image (submission, challenge, appeal, etc) for each image, we get a model of:

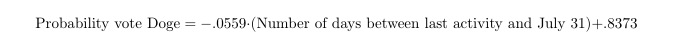
The p-value corresponding to whether the slope is negative is .0013, indicating strong statistical evidence that jurors have been less and less willing to vote "doge" on these images over time.  

Indeed, most of the more recent cases have been unanimously voted as "not doge." Hence, when jurors were faced with a situation which could be interpreted as ambiguous, after some early contentious cases, a sort of precedent was established. Then submitters, challengers, and jurors can all reasonably predict how these images will be ruled going forward.  

Analysis of whether jurors look at already cast votes on the blockchain

In the current implementation of the Doge pilot, votes are visible in the blockchain as soon as they are cast. (In the long run, we intend to have some kind of commit-and-reveal mechanism so that votes stay concealed during the voting period.) This means that the last few people to vote on each case could check the previous votes in an attempt to be coherent.

An important note is that payoffs and penalties to jurors for being coherent or not are based on the ultimate outcome of the case. So making sure that you are voting with the majority of people who have already voted is not necessarily a good strategy if you think that their decision will be appealed.

Indeed, if you believe cases that are decided incorrectly will be appealed, you should try to vote with how you think a large number as-yet-unknown  "ideal jurors" would vote in a future appeal, regardless of the current vote total.

Nevertheless, if there are very few incoherent votes that are cast too late to make a difference in the outcome of a given round, we could view that as evidence that jurors are in fact looking in the blockchain for the other votes.

Excluding the cases where there were ongoing p+epsilon attacks, up through disputeID 148 there were 16 non-unanimous decisions (2-1) in the first round of voting and 10 non-unanimous decisions in the second round (either 4-3, 5-2, or 6-1). In total, over these 26 voting rounds, 35 total votes were cast on the losing side. Of these 35 votes, 11 were cast after the winning side had a majority.  

If we believe a hypothesis where jurors are not looking at previous votes in the blockchain, then we might expect the order of "doge" and "not doge" votes in a given case to be random. Namely, in a given 2-1 decision for doge, we should expect:

doge - doge - not doge

doge - not doge - doge  and

not doge - doge - doge  

to be equally likely. Thus, we should see the "doge - doge - not doge" situation, where a juror has voted incoherently after the outcome of the round is already set, one-third of the time.  

If the two votes that voted  "doge" were attributed to the same juror, then "doge - not doge - doge" is not possible as the address casts all of its votes together. So in such situations, if the order the votes were cast in was random, we would expect:

doge - doge - not doge and

not doge - doge - doge

to occur with equal frequency. So "doge - doge - not doge" would occur half of the time.

One can reason similarly for the appeal round, for example we had a 2-5 "not doge" decision where there were five distinct juror addresses that voted:

A (2 votes) doge

B (2 votes) not doge

C (1 vote) not doge

D (1 vote) not doge

E (1 vote) not doge

There are 5! many ways the votes of A, B, C, D, and E could be ordered. Of them, in order for there to have been a "doge" vote after there were already 4 "not doge" votes, B and two out of three of C, D, and E must have voted in the first three spots in some order. There are

many such orders. So, if the order of A, B, C, D, and E was random, there would be a

chance of two incoherent votes being cast after the majority is decided, and a .7 chance of zero incoherent votes being cast after the majority is decided.

(Caveats: It is, of course, possible that we have some subset of contrarian jurors who just also happen to log-on at the beginning of each voting period. So then the dissenting votes would be concentrated among the first votes in each case even if jurors are not looking at the cast votes on the blockchain. Considering the diversity of the images voting on and variation of exactly what time each voting period starts, we assume such effects to be negligible. Also we will assume that the order of the votes is independent from one case to another. In practice, jurors typically vote all of the cases for which they are drawn at the same time. So if the same person tends to be incoherent, their incoherences in cases in the same round will likely be in similar positions in the voting order. However, as these non-unanimous cases were spread out over many periods and which jurors were incoherent varied, we expect any non-independence from this phenomenon to be negligible as well.)  

Reasoning like this for each of the non-unanimous results we had, taking into account the number of votes that was controlled by each address in each case and assuming that the order of the votes is independent from one case to another, the distribution for how many incoherent votes cast after the majority had been determined we should have observed over random choices for the possible orders of votes is as follows :

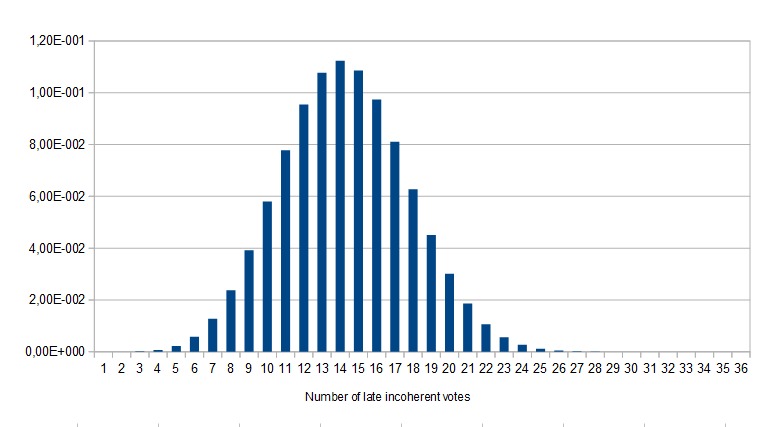
Again, we observed 11 such votes. The expected value of this distribution is 13.250, so slightly fewer late incoherent votes were observed than what was expected, but the p-value for our observation was .315716. So, at least so far, we do not have convincing statistical evidence that jurors were consulting the blockchain for votes already cast before ruling. (Of course, with enough additional data, it is possible that we could yet see evidence of such behaviour. This test gives us a measure to notice if and when enough jurors look at previous votes before voting themselves to be statistically noticeable.)

Conclusions

In the two previous articles of this series we have seen that the Doges on Trial pilot has shown a fair amount of resistance to 51% attacks and p+epsilon attacks. In this article, we have further observed resistance to lazy voting attacks, and our discussion regarding the order of coherent and incoherent votes gives a sense of the pilot's sensitivity to pre-revelation attacks.

Moreover, we have begun to observe effects related to the influence of evidence and the development of precedents. Such phenomena are important to the stability and predictability that should underlie useful dispute resolution systems, and we expect to further study such effects going forward.

Join Kleros!

Join the community chat on Telegram.

Visit our website.

Follow us on Twitter.

Join our Slack for developer conversations.

Contribute on Github.