Doges On Trial Curated List Observations Part 2 - Deep Dive Edition.

This is the second article in a three article series analysing user behaviour in Kleros' Doges on Trial pilot. In the first article, we've made some general observations and we looked at the distribution of juror voting.

In this article, we will look at various efforts to bribe the jurors of the Doge pilot. Kleros is based on the idea that complicated and lengthy disputes can be resolved in a way that reflects the opinions of a large pool of token holders – and is hence as difficult to attack as it is to corrupt a majority of the whole pool – while not excessively duplicating juror time and effort. This is done by randomly choosing an initial small panel of jurors and allowing appeals that pull in more and more jurors.

While it may not seem to be hard to bribe two out of three jurors in an initial round, actually changing the outcome of the case requires being able to maintain such an attack with more and more jurors during the appeals. We look at how such efforts fared in the Doges on Trial pilot.

Simple non-smart contract based bribes

There were a number of "traditional" bribes offered to jurors over the course of the Doges on Trial pilot. Would-be attackers typically put a text in their submitted image promising a portion of the payout they would receive to jurors who vote with them.

These attacks did not manage to buy the votes of very many jurors. This is perhaps unsurprising as, so far, their payouts have not been guaranteed by smart contracts. So, these attacks required the jurors to trust that the attacker would actually pay them.

What is more interesting is how the jurors responded to a series of p+epsilon attacks, a number of which were launched on the Doges on Trial pilot with payment guaranteed by smart contracts.

Analysis of p+epsilon attacks

A p+epsilon attack is a special kind of bribe, paid out on the condition that the attacker loses, thus warping the incentives of Schelling point-based systems. (See the discussion of V. Buterin that introduced this attack.)

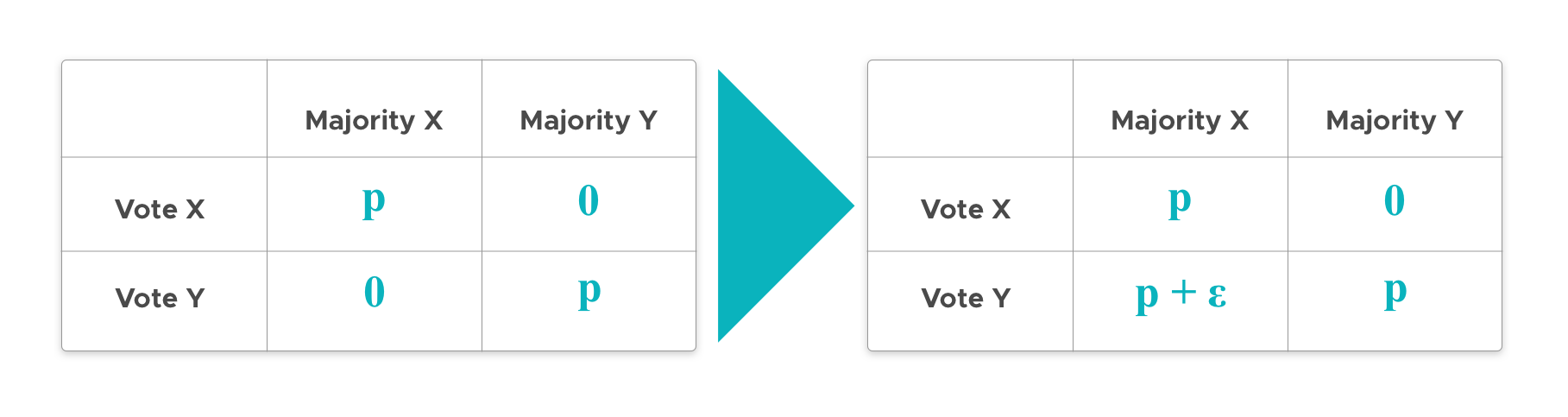
Let's suppose an attacker wants choice Y to win. In the simplest possible Schelling point system, voters are rewarded with p if they are coherent and get nothing if they are incoherent. Then the attacker offers p+epsilon to voters who vote Y if X wins.

This way, if a voter thinks X will be the majority decision, she will be better off voting Y to get the bribe. If she thinks Y will be the major decision, she is better off voting Y to be coherent and get p. So, either way she gets at least as much by voting Y as by voting X, i.e. voting Y is a “can't lose” strategy. Note if the majority votes Y, then the attacker does not have to pay out any bribes. So, in a context of perfectly economically rational voters, the attack should always succeed and an attacker has a free way of hijacking the incentives of the system.  

(Note: if a voter with a single vote knows that their vote is decisive, then they get p either way they vote by being coherent. If a juror has many votes that she knows include the decisive vote – or if many jurors that have the decisive vote between them work together in a way that they can trust each other to vote in certain ways, such as by committing large deposits to a smart contract that are slashed if they do not vote as instructed – then it is profitable to split up these votes in a way such that the attacker loses narrowly. However, note if a juror believes that a case will be appealed, then there is no one in that round whose vote decides the ultimate outcome, so it is always strictly in that juror's interest to accept the bribe.)  

In Kleros, the payoff table is slightly more complicated because the amounts jurors are rewarded for coherence depends on how many jurors are incoherent:  

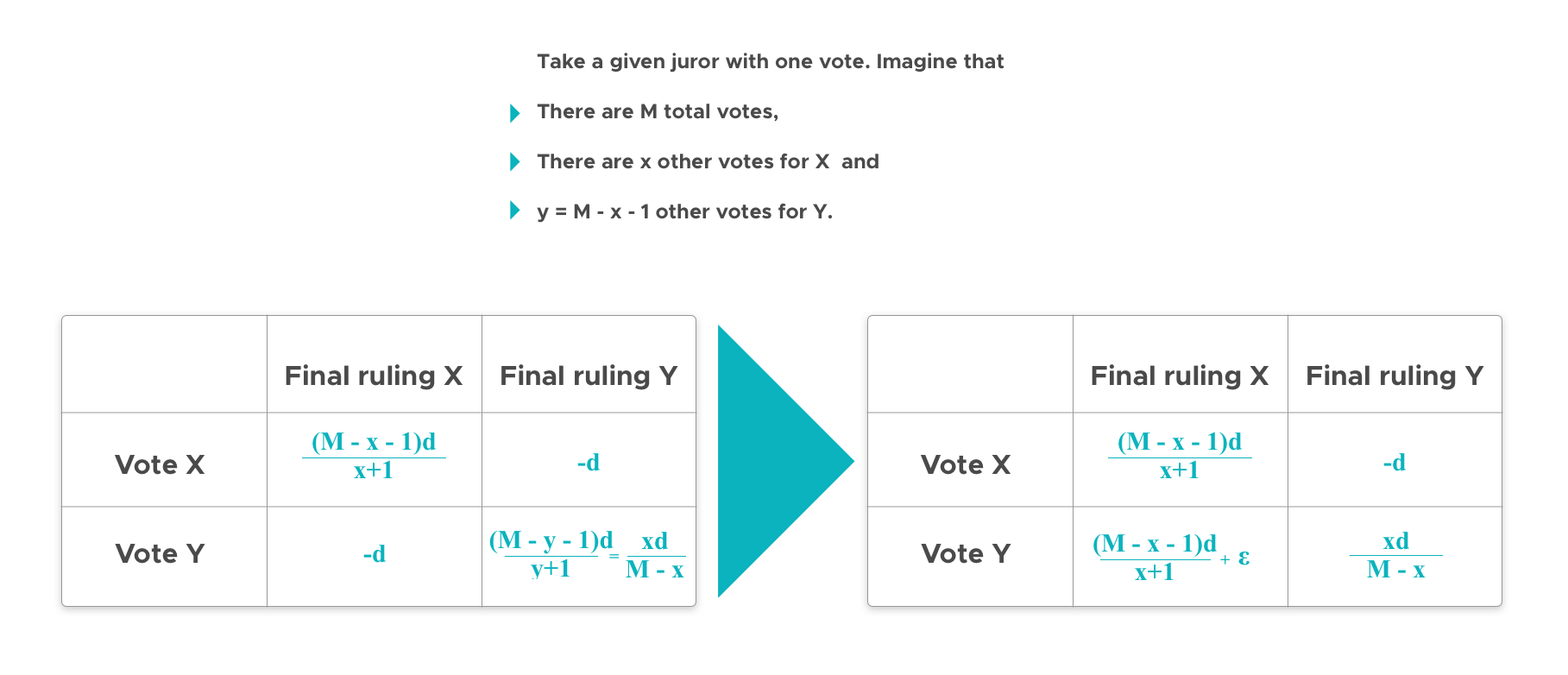
If the number of other votes for “not doge” is zero, namely if everyone in a given round accepts the bribe except you, but “not doge” eventually wins anyway in appeal, then the coherence payout for being the lone voice of reason in your round is the sum of all the other jurors in that round (M-1)d. If an attacker wants to incentivize jurors to accept the bribe, she must lock up enough PNK that in the worst case for her, where in every round except the last jurors unanimously vote Y but then X is voted narrowly in the last round, she can pay each of the jurors in these non-ultimate rounds enough so they are not encouraged to defect in hopes of getting the (M-1)d lone voice of reason bonus. Hence the attacker must lock up O(M^2) PNK; as M, the number of votes per round grows exponentially in the number of rounds, thus the attacker required lockup quickly becomes unviable.  

A solution to this problem from the perspective of the attacker is to only offer the bribe to jurors who vote in the round that winds up being decisive. This way, there is no subsequent round to prove that a “lone voice of reason” from this round was right. Such an attack was conducted in disputeID 94. The limitation of such an attack is that jurors are only incentivized to accept the bribe if 1) they believe they are in the last round or 2) they think the attack will ultimately succeed and they should vote with the attacker to be coherent.

So, if a juror thinks that there is likely to be an appeal and that the attacker will ultimately lose, they will not accept the bribe. In particular, voting with the attacker ceases to be a can't lose strategy in rounds that are not guaranteed to be terminal. DisputeID 94 was appealed five times, which is the maximum number of appeals that was possible in the Doge pilot (in more meaningful situations this parameter will likely be set to be much larger). Jurors in the sixth round of disputeID 94 knew that they were in the last round, so in that round this attack functioned like a standard “can't lose if you accept the bribe” p+epsilon attack.

To summarize, the p+epsilon attacks launched were for disputeIDs 70, 71, 73, 74, 75, and 76, smart contracts were deployed offering the bribe to jurors in rounds one and two for various choices of epsilon. In disputeID 94, the bribe was offered to jurors in the last round, which was unknown in advance, but in the sixth round it is impossible to appeal further, so jurors in that round knew the bribe was offered to them.

In some of the rounds there were relatively high rates of no-show jurors who were selected but didn't vote. In round 5 of disputeID 94 this was due to a technical problem in the Kleros juror interface. In the second round of disputeIDs 70, 71, 73, 74, 75, and 76 (which were conducted in parallel), this seems to have been due to abnormally high gas prices on the Ethereum network.

All of the images of these cats used in these submissions were created by Svetlana Petrova & Zarathustra the Cat. More information about their work can be found on FatCatArt.com

Note – in disputeID 75 the attack succeeded through rounds 1 and 2; it was then appealed by a member of the community to go to a third round where there was no longer a bribe offered and it lost 0-14 in this round.

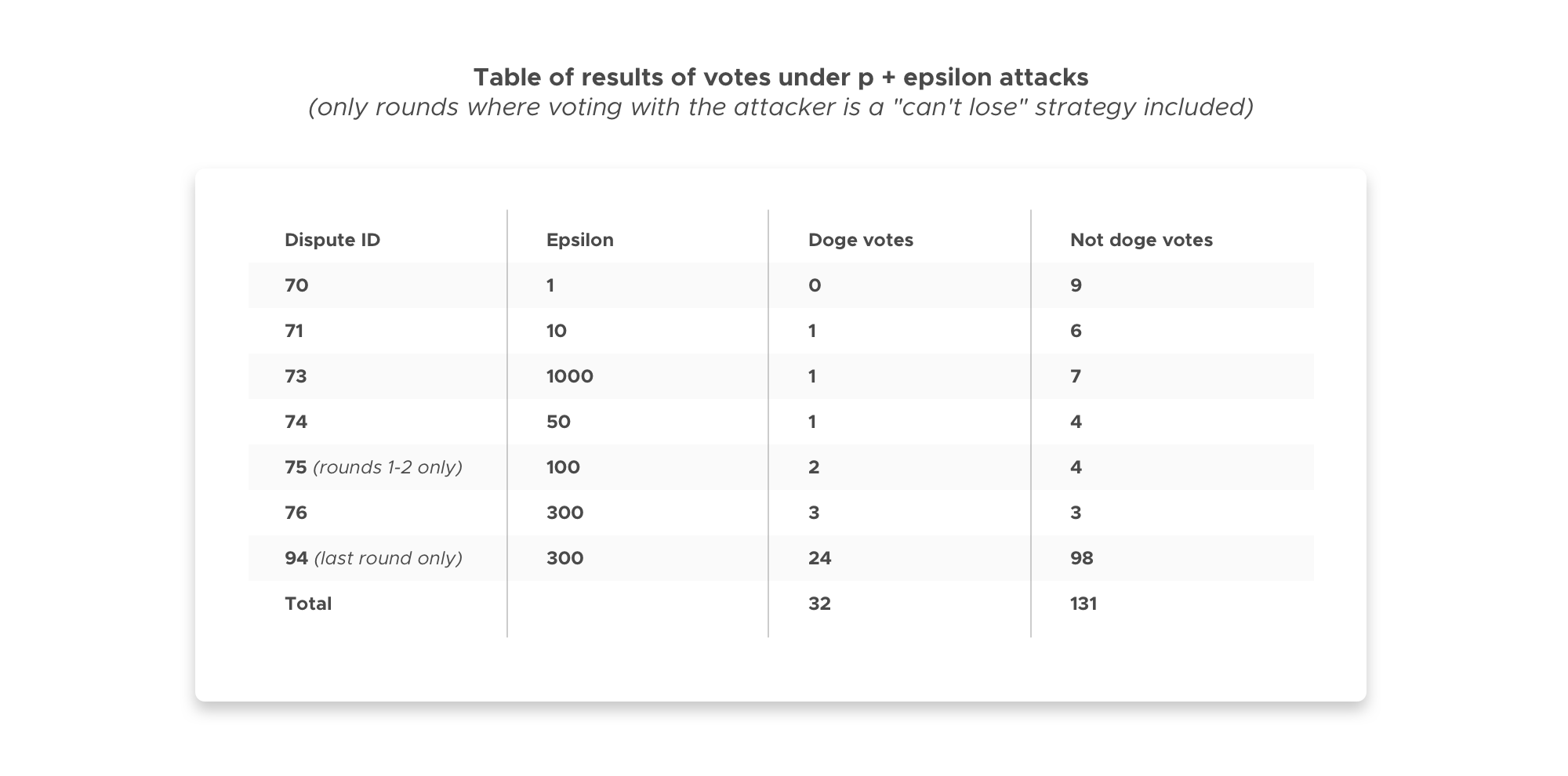
A few points on disputeID 94 - in addition to the vote totals in the table, we had the additional votes during early rounds when taking the bribe was not a "can't lose" strategy for jurors:

First five rounds (when bribe was not guaranteed): 31 doge, 77 not doge

First two rounds (when bribe contract was not deployed yet): 1 doge, 8 not doge

Rounds 3-5 (when contract was deployed but bribe not guaranteed): 30 doge, 69 not doge

Under the Kleros system, as long as the majority of PNK belongs to people who would rule honestly on a given case, that case would be ruled correctly and any attackers would be defeated if the case is appealed enough times.

Thus, when considering the danger of these p+epsilon attacks, we are mostly concerned with whether 50% of the PNK correspond to people that would accept the bribe. The juror selection mechanism makes independent, random choices of PNK to choose the jurors. So it makes sense to imagine that each given PNK would vote one way or the other if presented with a given p+epsilon attack, so there is some percentage of all PNK that would accept the bribe. Hence, the number of votes in a given round of that attack should be distributed as Binomial(number of jurors, y). Then we can ask if the number of votes seen accepting the bribe can realistically occur by random chance under the null hypothesis that exactly y=50% of the PNK would take the bribe. Taking the last round of disputeID 94 alone we see if X~Binomial(122,.5), then Prob(X <= 24)< 0.000001. Similarly, if we consider all of the guaranteed p+epsilon bribes together, we see if X~Binomial(163,.5), then Prob(X<=33)< 0.000001.

Here we have considered the underlying population we are studying to be the PNK. However, we are indirectly making claims about the people who have deposited those PNK, which as we saw in the previous article represent a total of 49 distinct addresses. Looking at the jurors who were drawn multiple times for different p+epsilon cases, it appears that for the most part jurors are either 1) always willing to accept the bribe regardless of the amount 2) always unwilling to accept the bribe at any of the amounts offered so far. Indeed, of the 10 jurors who were selected to make at least two distinct votes on p+epsilon cases (on different cases or even on different rounds of the same case, even including the early rounds of disputeID 94), only two of them voted each of “doge” and “not doge” at least once on such cases. (One of these jurors refused the epsilon=1 bribe but accepted bribes for epsilon=300. The other voted “doge” in round 5 of dispute 94 and voted “not doge” in round 6, which is actually the opposite of what one might expect as in round 6, the decision was known to be in its last round so the bribe was guaranteed.)

So, the uncertainty of looking at the number of votes accepting the bribe as binomial may actually be unwarranted and we could think of disputeID 94 as having taken something more akin to a census of jurors participating in the pilot. If jurors had shown more sensitivity to changing their vote based on the amount of epsilon, it would make sense to perform a logistic regression to model this variation; however considering the repeat jurors' constancy in accepting bribes or not, this does not seem justified.

So we are left with the question of why jurors did not accept the p+epsilon bribes at a higher rate. There are a few possible explanations. The first is simply that the current pool of jurors is simply too altruistic. People engaging in the pilot are generally people who are interested in the underlying ideas of Kleros and want the project to succeed. As the juror pool evolves this may no longer be the case and future jurors may be more susceptible to taking bribes including p+epsilon bribes.

A second possibility is that the cognitive cost of understanding the bribe was not worth it to the jurors; namely, while it may be economically rational to accept the bribe, you are only convinced of that after you go read Vitalik's blog post. A bribe like the "last round" p+epsilon attack of disputeID 94 is even a notch more complicated. Similarly, there are variants on p+epsilon attacks where an attacker can offer bribes up to some cap as a way of getting around the growth of the attacker lockup imposed by our distribution mechanism. In such an attack, the equilibrium strategy is for jurors to adopt a mixed strategy, accepting the bribe with probability close to but less than 1 and voting against the attacker otherwise. Understanding what the “rational” strategy in such a situation is and executing it appropriately requires an even higher cognitive cost.

Moreover, in the consideration of cognitive costs, while the bribes were enforced via smart contract, unless she carefully studies the code herself, a juror might not necessarily be convinced that there is not a bug or even a trapdoor in that contract to allow the attacker to not pay. Often in the crypto space, reputable auditors are used to review smart contracts. However, who will trust an attackers' auditor?

However, when providing feedback on why they voted the way they did, several jurors indicated that the bribes they were offered were simply too small, implying a threshold beyond which they would be more willing to consider the bribe. Ideally, in order to corrupt a jury it would require very large bribes relative to the amount at stake in the case. It is thus somewhat unclear how jurors would respond to a p+epsilon attack with a large epsilon if they thought that, because the epsilon was so large, the attack would probably succeed and they wouldn't ultimately get a bribe.

Conclusions

We see that so far jurors have been pretty resistant to accepting bribes. In particular, similar bribe attacks would appear likely to fail in the conditions of the current juror pool, which might provide enough of a deterrent to discourage some attackers from attempting a bribe at all. One can provide reasonable explanations for their behaviour based on a mix of rational and altruistic motivations. Going forward, we will continue to monitor how jurors react to such bribe attacks, particularly as the juror pool grows and diversifies, and what that implies about the security level of Kleros.

In the final article of this series we will take a detailed look at a number of other questions related to juror behaviour.

Join Kleros!

Join the community chat on Telegram.

Visit our website.

Follow us on Twitter.

Join our Slack for developer conversations.

Contribute on Github.