Voting and Incentive Systems in Kleros Cases with Numeric Outcomes
In this research piece, Dr. William George demonstrates the different voting and incentive models of Kleros V2 that will be significantly increase the adaptability of the protocol.

Most Kleros disputes to date have offered jurors a choice that is more or less binary. Jurors vote that a submission to a curated list such as Tokens or Proof-of-Humanity should be included in the list or not. Jurors vote on whether a decentralized insurance policy should pay out or not.
However, for some disputes, one would want the jurors to be able to produce more nuanced outcomes. An important special case of disputes that require non-binary outcomes is when an appropriate ruling for the dispute should take the form of a number. Indeed, this category includes many important use cases:
• In a dispute between a freelancer Bob and a small business owner Alice over whether Bob deserves to be paid for a task. If there are issues with Bob's work and he shouldn't be paid the full amount for the task, it may still be appropriate to pay him some partial amount. Then, Kleros jurors would need to determine what this appropriate compensation for Bob is, which could be, for example, 50% of the original amount, 70% of the original amount, or something else.
• If a holder of an insurance policy makes a claim that is contested by the insurance company, this can lead to a dispute where jurors need to determine the appropriate amount of compensation that should be paid out. This could facilitate the use of Kleros for insurance policies covering anything from personal injury to smart contract bugs.
• Kleros jurors could be called upon to determine the appropriate compensation to award in cases where a patent or some other intellectual property is infringed. Particularly, legal researchers have imagined how Kleros and similar systems could be used in IP questions related to NFTs.
• One could imagine a social network platform where, in order to post content, users need to place a deposit asserting that the content respects the terms and conditions of the platform. Then, for example, a user that is a victim of harassment or abusive comments could be paid compensation from the deposits of the harasser. Once again, Kleros jurors could determine the exact amount of compensation that is appropriate.
In such disputes, the role of Kleros jurors resembles that of "damage qualification experts" who provide monetary estimates of damages in traditional dispute resolution. In this article, we will discuss a few voting and incentive schemes that could be used to deal with these types of disputes.
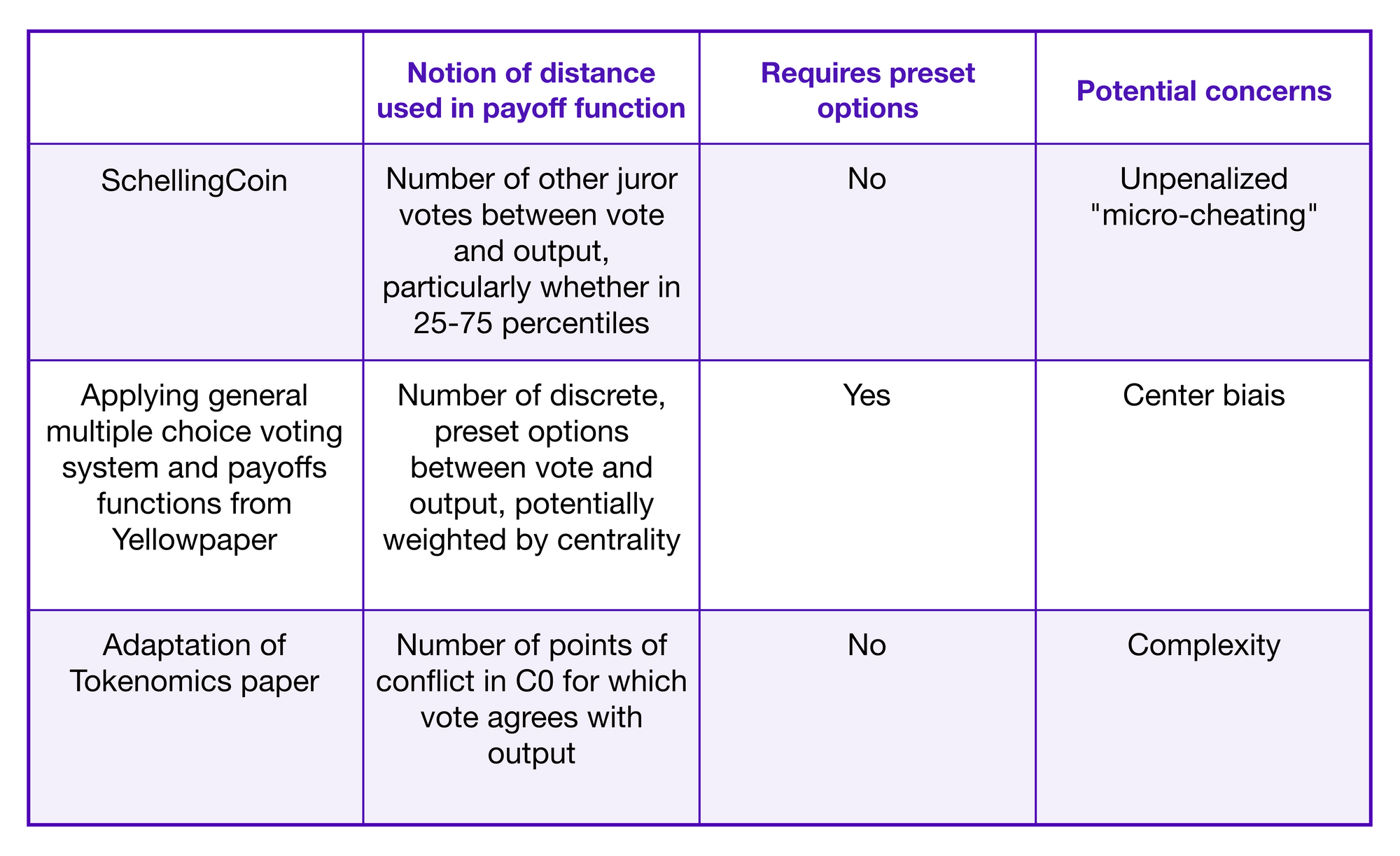
Recap of SchellingCoin
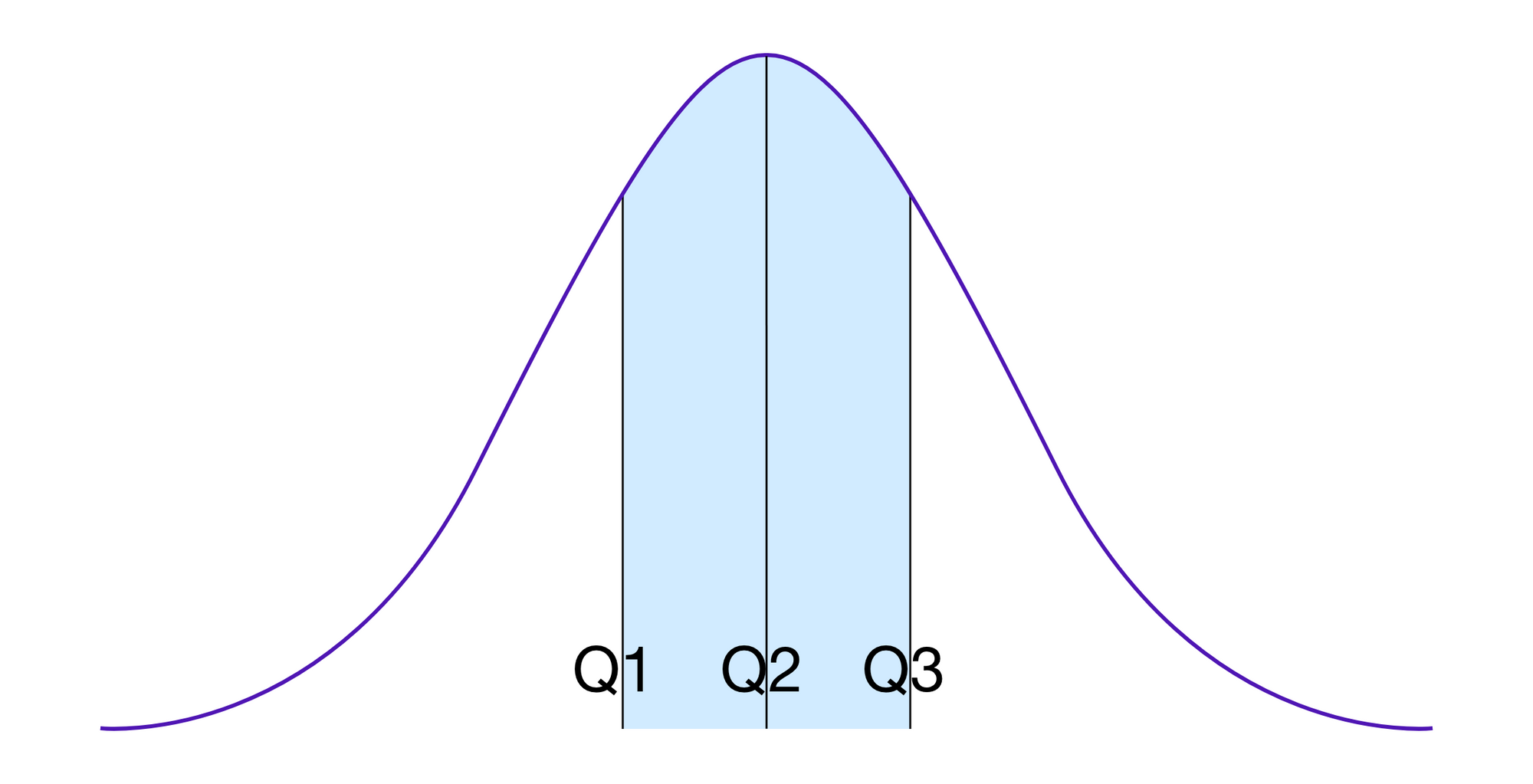
The setup is closely related to that of one of the earliest inspirations of Kleros in the crypto-space: a 2014 Vitalik article that presents an idea that he calls SchellingCoin. Vitalik describes a Schelling-point-based system to produce a price feed for the price of ETH in USD. Specifically, in the system he proposes, a smart contract takes the median of submitted prices as the value it should use and rewards users who submit prices within the 25-75 percentile range.
One issue that he describes in this system is the risk of "micro-cheating": an attacker might try to provide values that are systematically slightly higher or lower than the true value. The issue is that there will generally be some natural variation in the distribution of the values that honest participants propose to the system, and by providing values that are on one or the other end of this spectrum of "normal" responses, the attacker can nudge the median in a desired direction.
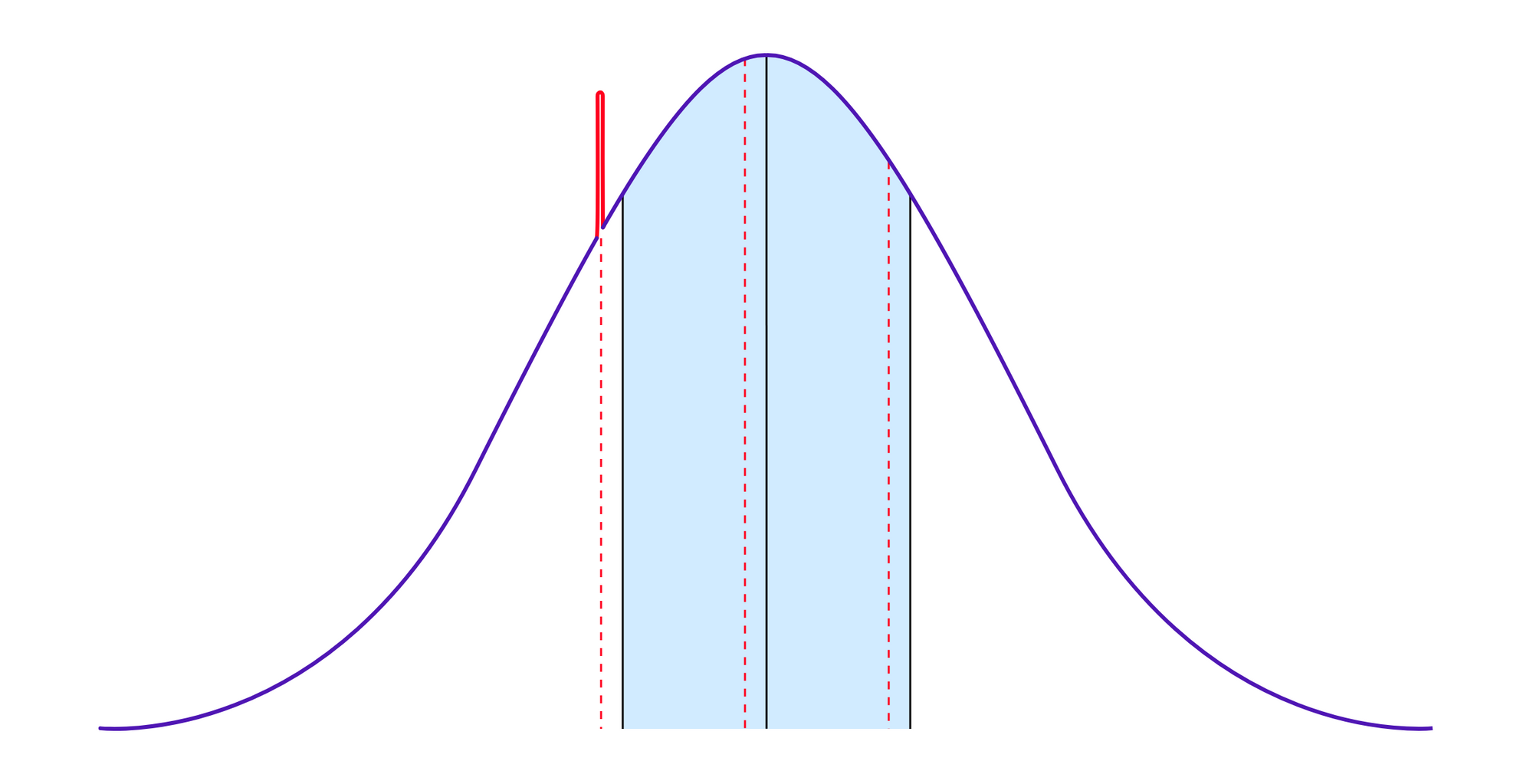
Potentially, the attacker can even nudge the median in this way while remaining in the 25-75 percentile range and not being penalized under Vitalik's SchellingCoin scheme. A slightly more sophisticated reward function could take into account exactly how far from the median a submitted value is with rewards that decrease continuously the further the user's value is from the median. Then any deviation would at least have some cost.
However, having continuously varying penalties for small deviations gives a lot of space to an attacker to determine when it is worth it to her to suffer some small losses in her rewards in exchange for slightly changing the collective outcome.
Contrast this with the stark incentive structures of other cryptoeconomic systems where:
• If an attack fails because less than some threshold percentage of the votes vote with the attacker, then the attack has no effect on the collective outcome. For example, in the Ethereum consensus layer, if less than 33% of attestors maliciously fail to attest blocks, then there is no effect. (Whereas if more than 33% but less than 50% of attestors act maliciously, they can delay the finalization of blocks even as new blocks are added to the chain.)
• As the number of votes of an attacker grows and her attack becomes more threatening, the stakes for the attacker should grow. Ideally, this growth should be super-linear in the number of votes that the attacker has, so that an attack that barely fails is catastrophically expensive. On the other hand, if users whose votes aren't correlated according to some kind of attack pattern make honest mistakes, their penalties shouldn't be too severe. This type of reasoning motivates the fact that slashing penalties in Ethereum consensus are higher if many other validators have also recently been slashed.
Part of what makes voting and incentivization of Schelling-point systems for numeric outcomes hard is that it can be difficult for such a system to distinguish between 1) situations where the variations in the values that are submitted to it are just due to noise and natural variability in how honest actors can observe a value and 2) situations where honest actors would provide relatively uniform answers, but there is an ongoing attack.
In the first case, to the degree that all the voters have essentially provided the "right" answer according to a high level of precision with only negligible variations between the responses, you might want to reward everyone. At least you probably don't want to enforce severe penalties on voters whose vote was marginally further from the median due to noise. In current Kleros cases, if all of the jurors agree on an answer, none of them are penalized and they all share the rewards.
However, in order to only penalize voters when the deviation between their votes is "meaningful", rather than always penalizing some fixed percentage of the voters, the system needs a measure to determine what a meaningful variation from the median is. However, even if you ask similar questions repeatedly, e.g. one takes a price oracle for the same pair of currencies or you ask jurors to rule on a category of similar disputes, there will be times of high variability where it is natural for honest answers to be more spread out.
If a system determines how high its stakes should be based on how big of a (percent) change in the outcome could result from slightly different votes participants, then at what point is the possible change big enough that the system should see it as being sufficiently "important" to raise the stakes for the participants?
Discrete Choices and Social Choice Theory
In the SchellingCoin system above users are just asked to submit a number and are not provided with any specific values to choose between. However, one could instead have some set of possible numeric outcomes from which jurors choose.
Bob the freelancer and Alice the small business owner could agree when setting up the smart contract that handles Bob's payment that in the event of a dispute Kleros jurors would choose between:
a) pay Bob the full amount for the completion of the task,
b) pay Bob 70% and give a 30% refund to Alice,
c) pay Bob 50% and give a 50% refund to Alice, and
d) pay Bob 0% and give a 100% refund to Alice.
Now the question of how much of a change is big enough for the system to consider it important could just be that the result changes from one discrete outcome to another. The system now has a built-in notion of precision for what meaningfully different outcomes look like. Of course, this setting requires additional assumptions on the parties to the dispute – they have to provide this extra information on what multiple choices to consider.
Presenting a list of several outcomes like this for voters to choose between is a framework that is common in a lot of "voting situations", from national elections to voting for the Academy Awards. As such, one can draw on decades of research in the academic field of social choice theory which has considered how to design good voting systems for such settings.
In fact, the Kleros v1 smart contract already allows for the creation of disputes where jurors can choose from a pre-determined list of more than two outcomes. Indeed, all disputes have "Refuse to Arbitrate" as a potential outcome. So even in Kleros disputes whose main outcomes are as seemingly binary as "Accept submission in curated list" and "Reject submission from curated list", there is a third possible outcome.
However, jurors only tend to vote "Refuse to Arbitrate" in exceptional circumstances, and generally, when there have been more than two outcomes presented to Kleros jurors, the cases have been "de facto binary" with only two outcomes that have a serious chance of winning.
This is related to the fact that the current version of Kleros uses what is known as the Plurality or "First-past-the-post" voting rule. Namely, in a vote with multiple alternatives, the alternative that receives the most votes wins, even if it does not get a majority of the votes.
Thus, in a vote with more than two plausible outcomes, there is a risk of vote splitting. If the honest votes are split among several reasonable options, then the percentage of the vote that the winning answer will have will be reduced. This is particularly true if there are several options that are similar. Then, whereas an attacker needs at least half of the votes to force through a malicious answer in a binary dispute, in a vote with many possible outcomes she may only need to control a much smaller percentage of the votes in order to change the outcome.
Indeed, this effect can be particularly dangerous in a Schelling-point system as honest jurors that are confronted with many honest but similar options and one distinguished but incorrect option may vote for the distinguished but incorrect option expecting it to have a better chance of winning than any of the honest options. Thus, the distinguished but incorrect option offers an alternative Schelling-point.
For example, in an insurance case where the jurors can choose between several different payout amounts or they can choose to reject a claim entirely, the jurors could anticipate the vote being split between the different payout amounts and vote for the rejection of the claim as the only distinguished alternative. This could lead to the system being excessively severe.
Much of our research over the years has considered how Kleros can be adapted to handle nuanced, non-binary disputes where there are multiple plausible options for jurors to choose between.
One approach that we have considered is to allow jurors to provide a ranking of multiple outcomes. This is an approach that has been widely considered by social choice theorists in the context of political elections. Similar candidates splitting a vote is, of course, an issue for elections for president or member of parliament as well as for Kleros.
Social choice theorists have invented many different methods for converting the rankings provided by the voters into a collective result. A prominent example is the Borda count where ranking an outcome first gives it a certain number of points, ranking it second gives it a smaller number of points, etc with the winning option being the one that gets the most total points. Another important method is the Instant Runoff system where the voters' rankings are used to simulate a series of runoffs, with candidates who receive few first-place votes being eliminated and having their votes redistributed to the second-choice candidates of their voters.
We will briefly recall some ideas from social choice theory. First, we fix some notation. If a vote v ranks the outcome a higher than the outcome b, we write:
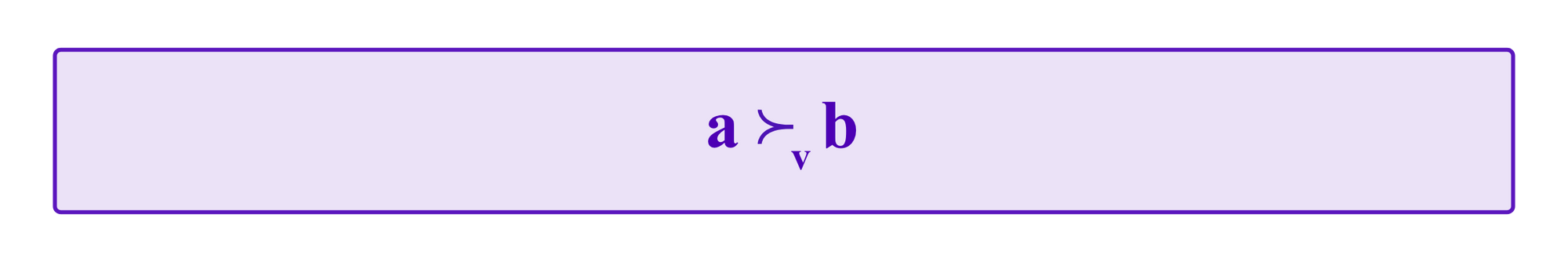
One particular property that a voting system can have is to be "Condorcet". A voting system is Condorcet if, whenever there exists some option a such that for any other alternative b a majority of all the votes v rank a ahead of b, then a must be the collective outcome. Namely, if an option a wins "pairwise" against all other options, then it should be the winning outcome. Formally, a system is Condorcet if whenever there exists a such that

for all options b≠a, a is the collective outcome.
This property is named for Nicolas de Condorcet, an 18th-century French mathematician who was a pioneer in social choice theory. Some reasonable voting systems have the Condorcet property while others do not. Indeed, it turns out that these different methods all have their advantages and disadvantages, with different types of strategic behavior and unexpected phenomena being present from one system to another.

The upcoming v2 of the Kleros court contract has been designed to offer greater modularity. Different courts will be able to have different voting and incentive systems adapted to the types of disputes that are decided in those courts. We expect cases where some finite list of options is presented to jurors to be a standard situation in the future, and as such we have done a lot of research to determine what voting and incentive systems are most appropriate for that module.
Generally, we think that voting systems where jurors rank the alternatives are a good approach for this situation. See Section 4.7 of the Kleros Yellowpaper for a summary of some of the tradeoffs between different voting and incentive systems that we have considered.
Now we can go back to our example dispute between Alice and Bob where the possible outcomes were:
a) pay Bob the full amount for the completion of the task,
b) pay Bob 70% and give a 30% refund to Alice,
c) pay Bob 50% and give a 50% refund to Alice, and
d) pay Bob 0% and give a 100% refund to Alice.
Essentially, the jurors are deciding between four numbers: 100, 70, 50, and 0, where this number represents what percentage of the amount Bob should be paid. Then, one can think of the options as inheriting the order of the numbers they correspond to. Namely, we say that one option is greater or less than another, with a > b > c > d.
This would not be the case if, for example, some of the possible outcomes were to give Bob a partial payment but other possible outcomes were to give Bob more time to finish the task. These different types of outcomes cannot be directly compared in the same way as it does not generally make sense to say that paying Bob 70% of the amount is "greater" or "less" than giving him a one-week extension to finish the task.
So in the special situation of numeric options, we now have two different types of ways of comparing the options. The curly inequality sign we considered above:
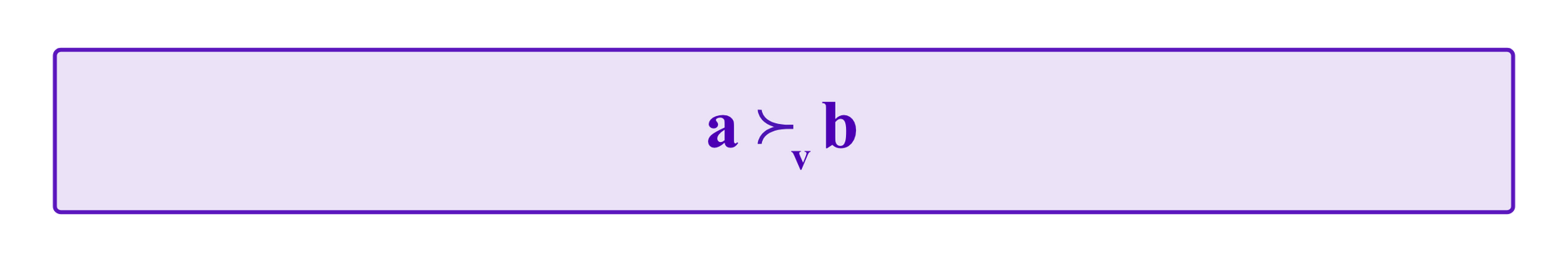
indicates that one option is higher placed than another in some vote v, whereas straight inequality signs such as a > b can be used to indicate that a is greater than b as a number.
The structure of being able to order the options as numbers interacts with how rankings provided by voters are aggregated into a collective outcome in interesting ways. Indeed, if a voter thinks that the appropriate outcome is for Bob to receive a payment of 50%, if she is being consistent she should think that it is more appropriate for Bob to receive a payment of 70% than for Bob to receive a payment of 100%. If one restricts to voters who have such consistent preferences, then one sees that the phenomena around aggregation of votes simplifies significantly.
Then, suppose that three possible outcomes a, b, and c are such that a > b > c as numbers. The consistency properties that we assume on our voters are the following: If some voter thinks outcome a is a better outcome than outcome b, she also thinks that b is a better outcome than outcome c. Similarly, if a voter thinks outcome c is a better outcome than outcome b, she also thinks that outcome b is a better outcome than outcome a.
Namely, if a > b > c, then:

Consider a vote with M voters. Suppose that the option a is the median of the first choices of these voters. Then it is not hard to see that any Condorcet voting system using ranked votes that satisfy the above consistency properties will select a as the collective outcome. To prove this, let b be any option other than a. Then, as numbers either one must have a > b or b > a.
Suppose we have a > b. Then, as a is the median of the voters' first choices, there are at least M/2 votes v whose first choice is greater than or equal to a. Namely,

However, we necessarily have

So by the consistency property, we have
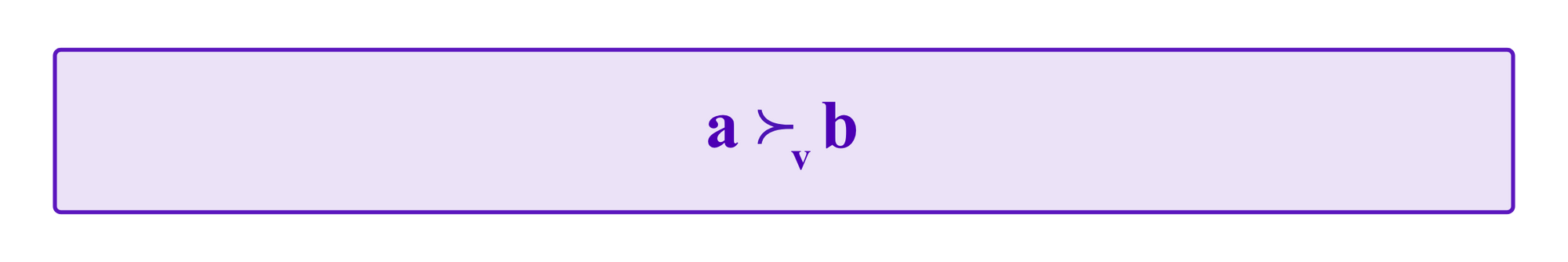
for each of these at least M/2 votes.
By a similar argument, if we suppose a < b, then there are at least M/2 votes v whose first choice is less than or equal to a, and we again use the consistency properties to see that
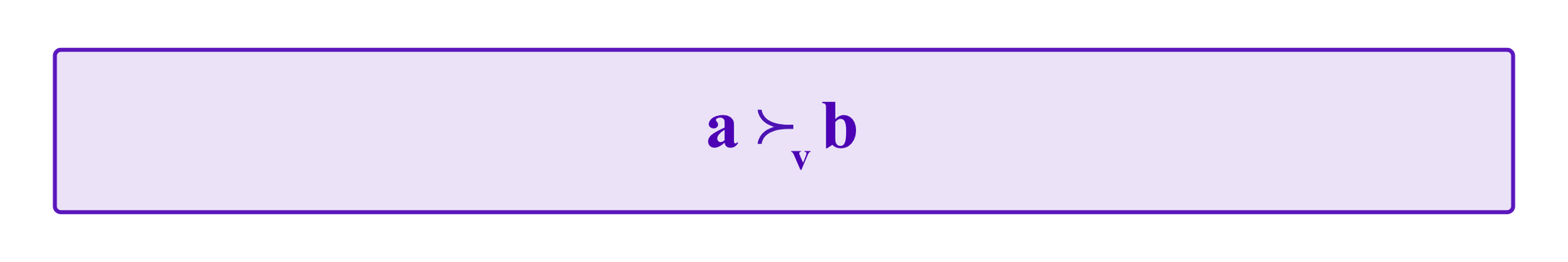
for these votes.
So, in the special case of discrete, numeric options, all of the Condorcet voting rules that we consider in Section 4.7 of the Kleros Yellowpaper turn into just taking the median option of the voters' first choices. (Strictly speaking, there can be some divergences if the median falls between two of the numeric options considered by jurors due, essentially, to a tie. Most prominent Condorcet voting systems would output one of the two tied options in this case.)
As a result, in this special case, the choices that a voter provides after her first choice do not contain any useful information for the aggregation of the collective outcome using a Condorcet method. So, actually, we can avoid asking voters for rankings at all and one can have the more familiar user experience of voters just providing a vote for a single option while still having all of the game theoretic advantages of using a Condorcet method.
Incentive systems
So it may seem that having non-binary disputes does not present significant complications as long as the options can all be thought of as numeric, allowing us to avoid the complicated tradeoffs that are considered in Section 4.7 of the Yellowpaper. Furthermore, it may seem that any Condorcet voting system is not so different from the SchellingCoin scheme as, in both cases, the winning answer is the median value.
However, for any voting system that might be used in Kleros, one also needs to keep in mind the formulas that determine the payoffs that jurors receive and whether they provide appropriate incentives for jurors. In a binary case, the current incentive system of splitting the arbitration fees and lost juror deposits between participants who vote for the winning option is natural. In a non-binary case where jurors may be more or less close to the winning outcome, it can make sense to reward jurors for being "partially coherent".
In the Kleros Yellowpaper, we have considered a variety of payoff functions assuming that jurors vote by ranking the outcomes. The approach taken in most of those functions is to reward or penalize the juror based on how high she ranks the outcome that wins the vote. We can see how these payoff functions applied to the special case where the options are numeric compare to the 25-75 percentile incentive scheme in SchellingCoin.
Suppose that we have a case where jurors choose between a set of outcomes A, where the total number of possible outcomes is |A|=n. Suppose a total arbitration fee of F is available to be split between the jurors in a given voting round and that each juror i places a deposit of D and submits a ranking vi of the n outcomes. (If jurors do not rank some outcome it is considered to be tied for last in their ranking with any other unranked outcomes.)
One of the voting systems drawn from social choice theory mentioned above can be used to determine a winning option w based on the submitted rankings. Then, a (somewhat simplified) example of the type of incentive system that we consider in the Yellowpaper would penalize a juror i who provides a vote of vi an amount of

Here the 1 in the sum on the right-hand side is an indicator function that gives the value of 1 when the condition in its subscript holds and 0 otherwise. Namely, the juror does not lose any part of her deposit if she ranks the winning option first and for each option that she places ahead of the winning option, she loses an amount of D/(n-1).
Then, the arbitration fees of F and the lost amounts from jurors' deposits are distributed to a given juror i according to how many options she correctly ranked below the winning option w compared to how many options the jurors collectively ranked below w. Namely, the juror i receives

in arbitration fees in ether and
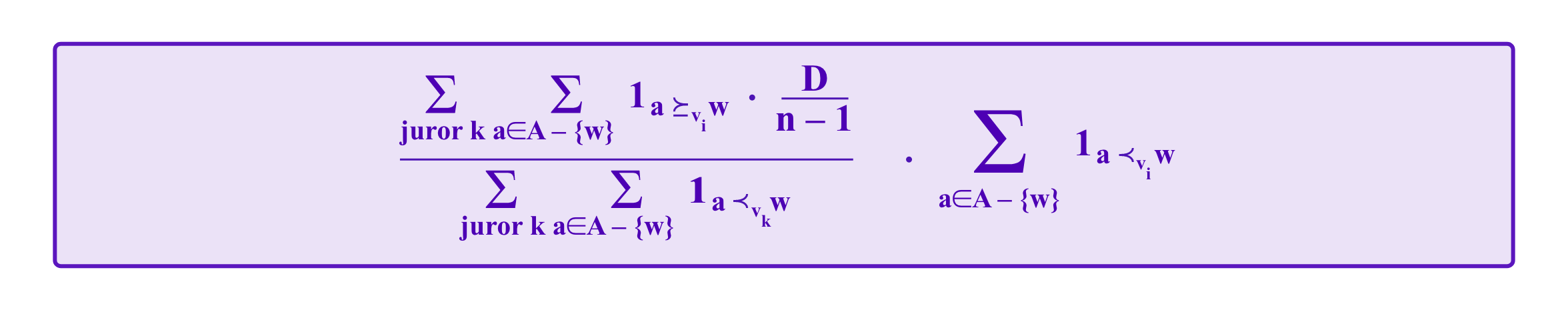
in redistributed PNK.
These formulas have several natural properties. A juror who votes for the winning answer receives the maximum payout and it turns out that a smart contract can be written so that the sums needed to compute a juror's payoff can be computed efficiently.
Moreover, as the jurors in a given voting round are essentially playing a fixed sum game, a juror who thinks that the round is going to resolve to an incorrect outcome that is likely to be reversed upon appeal has a that much greater incentive to stand her ground and vote for the answer she believes to be correct. We have seen that this "lone voice of reason" effect offers resistance to certain attacks.
We can consider what these formulas give when the options are numeric. Say we have a dispute with possible outcomes a, b, c, and d with a > b > c > d as numbers such as in the dispute between Alice and Bob above.
We concluded that for the sake of calculating the winner, it is enough for a juror to vote for a single option rather than provide a ranking of the outcomes. However, one can still think of a juror as having some implicit ranking of the outcomes that she believes is best even though she does not communicate the entire ranking. If the juror follows the consistency properties above, what do we know about what the outcome they vote for says about the ranking she has for the other options?
For example, if a juror votes a, then she is opting for an option at one of the numerical extremes. Then by the consistency properties, her preferences for the other options should be based on how far from a they are. Namely, the juror's belief should be that:
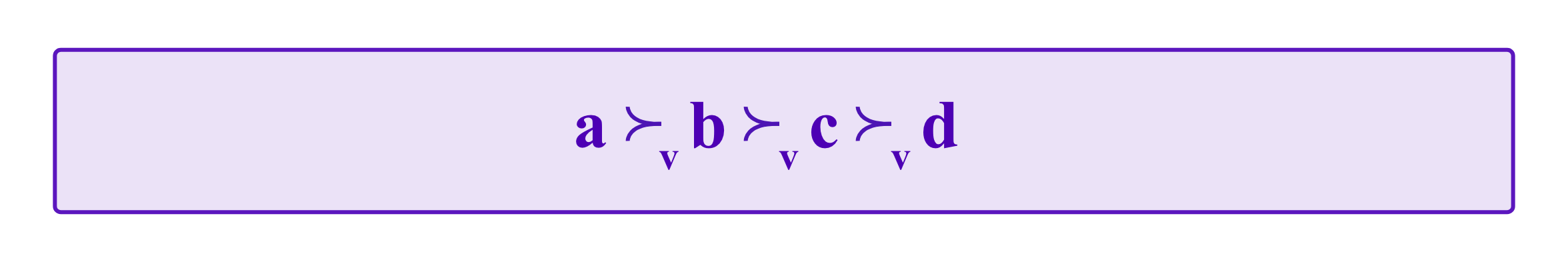
On the other hand, if a juror votes b, then it is not clear whether she prefers a or c. So we can only conclude that the juror's ranking would satisfy:
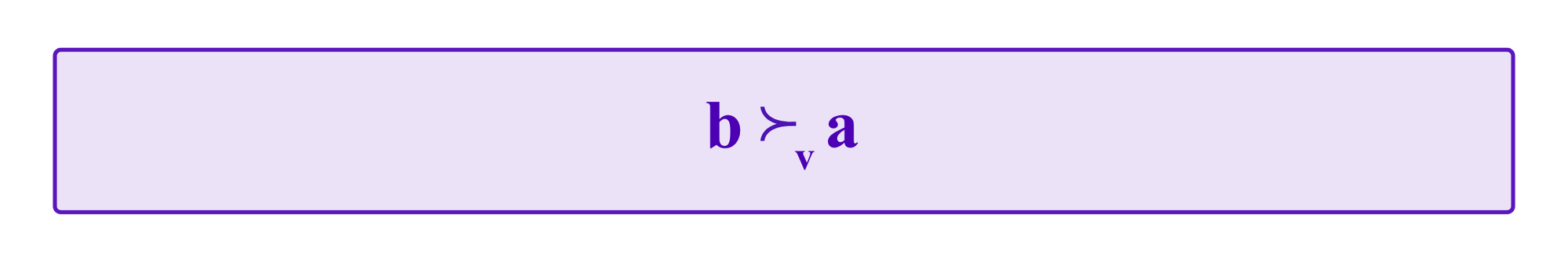
and
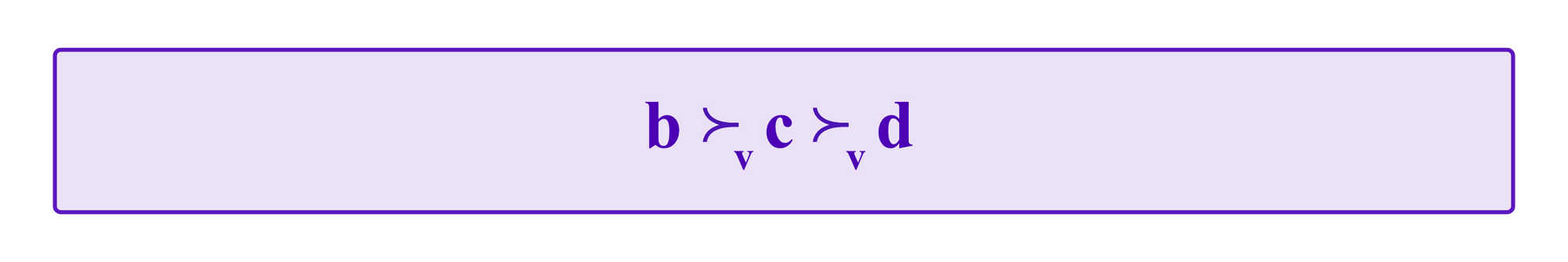
While this information about the juror's ranking is incomplete, it still tells us most of the terms that we would need to use to calculate the
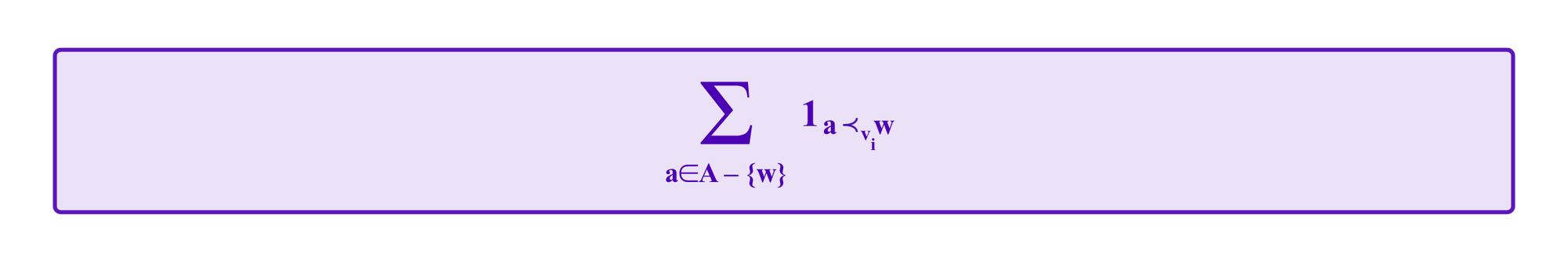
type sums in the payoff formulas that we have above for the general, non-binary option case.
In the sum as written in the formulas above, a voter whose vote does not include information about how the winning option is ranked is treated as if she ranked that option last. This encourages participants to rank as many options and hence provide as much information as possible, while still not requiring them to rank all of the options. In the situation where we are inferring the voter's preferences from a vote consisting of a single option by using the consistency properties, treating an option that we can't infer anything about as being ranked tied for last is somewhat harsh.
So imagine, if w is the winning option of the vote, that we replace the sums
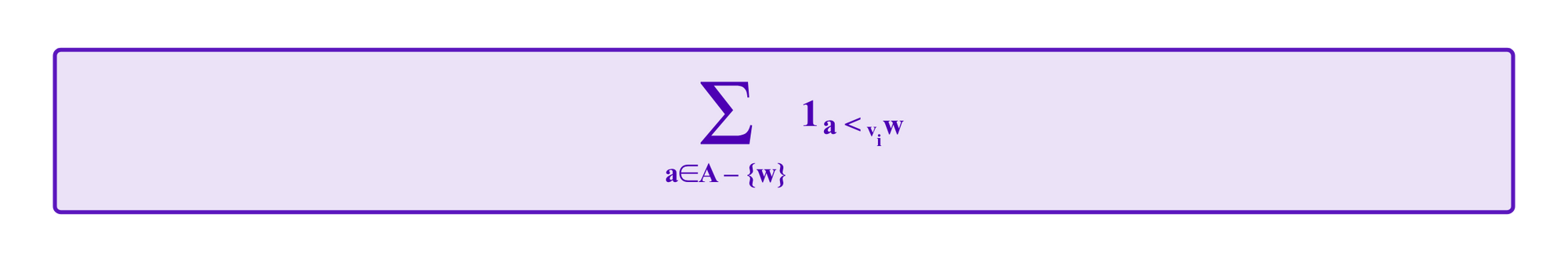
in the above formulas with values f(vi,w) that give one point to juror i for every option in A-{w} that i's vote implies (using the consistency properties) that she would rank behind w and gives a half-point to i for every option in A-{w} for which the consistency properties do not give information on how i would compare that option to w.
Then, again in the example where there are four options such that a > b > c > d numerically, we can compute a table of the values of f(vi,w) as follows:
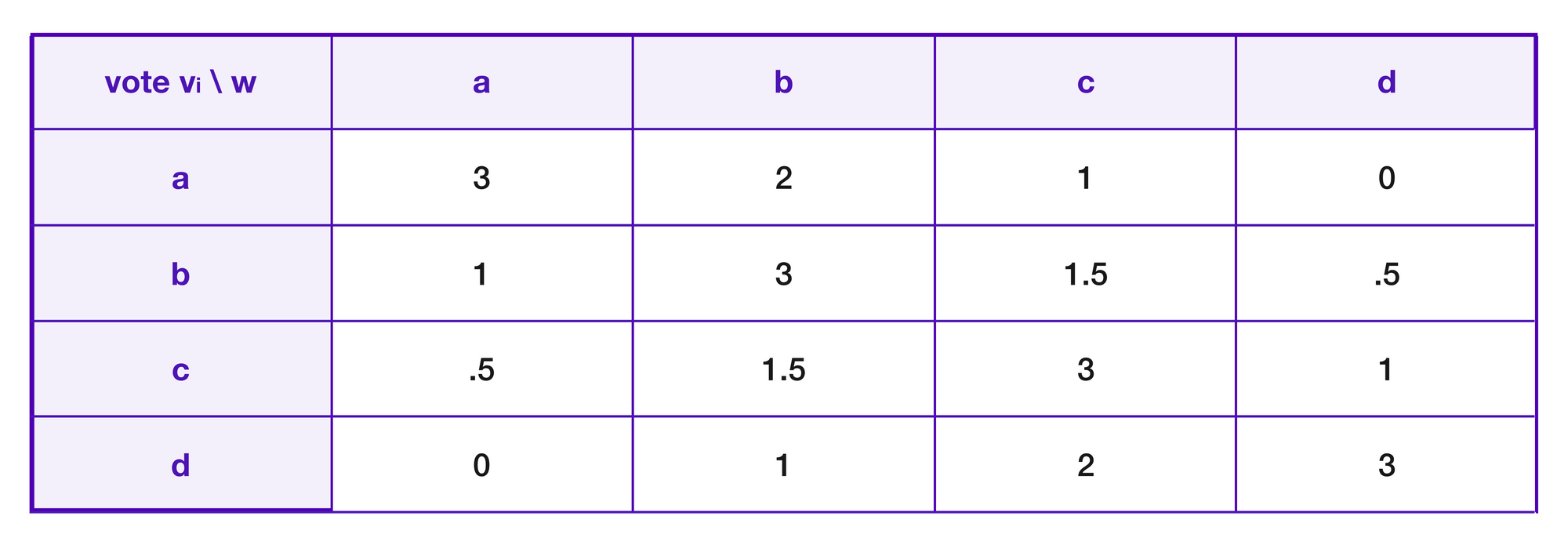
Then, a juror who votes vi loses
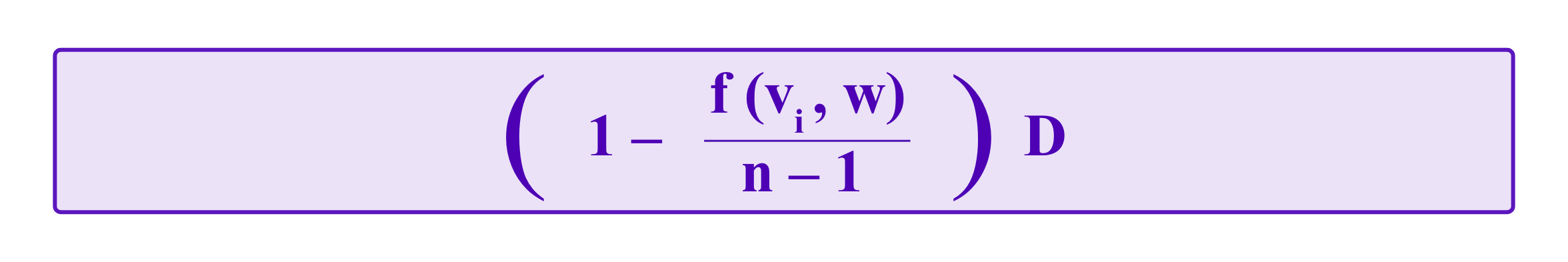
from her deposit, gains

in ether and gains
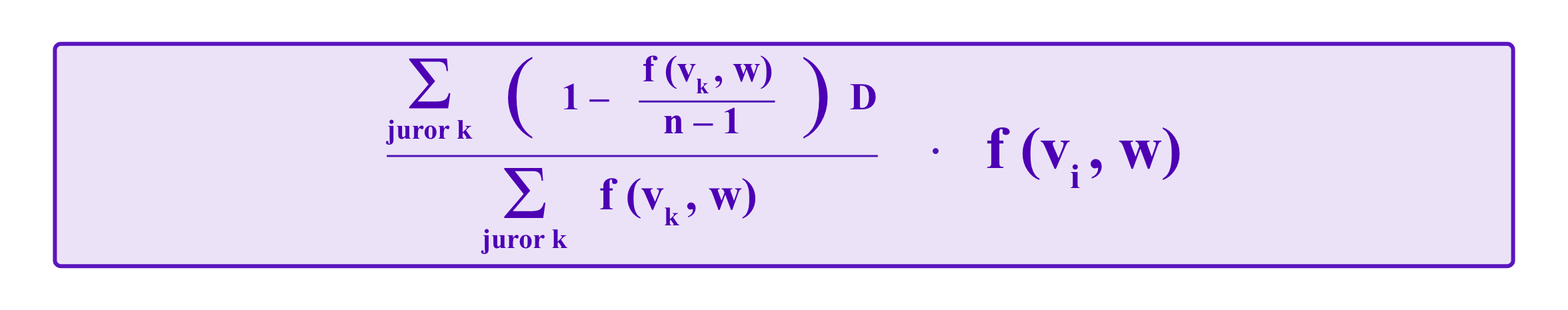
in redistributed PNK.
So this is, more or less, what the payoff functions described in the Yellowpaper give when applied to the situation where jurors decide between numeric options by voting for a single option. We saw that the voting system simplified into something very natural in the special case of numeric options and it is now worth asking whether these payoff formulas also give something that is appropriate in this special case.
Note that there are now floors on the cost imposed on an attacker that might attempt a "micro-cheating strategy". For example, voting for the option adjacent to the winner results in losing at least an extra D/3 from one's deposit versus voting for the winner.
On the other hand, an important issue in this approach is whether there is some systematic incentive for the jurors to vote for certain options based on whether they are more or less central in the numerical ordering.
If for example, it turned out that voting for the option that is in the middle numerically has a higher expected payoff, some jurors might be tempted to ignore the details of individual cases and just always vote for that option. This is a type of "lazy strategy". Note that this was not an issue for SchellingCoin as it doesn't provide a fixed notion of which values are more central than others absent actually putting in the work to think about how other voters will vote.
Some of the constraints that are used to calibrate parameters in Kleros are already motivated by making lazy strategies unprofitable. In particular, it is important to choose the deposits that jurors can lose high enough relative to the fees that they are paid so that random voting or other strategies that do not involve exerting an effort to analyze individual cases lose money on average.
Take pa, pb, pc, and pd to be the probabilities that a juror i attributes to the chance that a, b, c, and d respectively win the vote, still with the example situation of four numeric options such that a > b > c > d. Suppose that a juror believes that option a is correct, with the heuristic that this implies that she sees pa>pb>pc>pd.
In order to calculate the average payout of a juror for always voting for an option in the same numerical position, one would need to have some sense of the distribution of how other voters typically vote. In the absence of historical data for this type of case, consider the following heuristic: the juror i may err in her estimation of which outcome is the most likely to win, but she can expect the distribution of the votes of different votes around the winning outcome to have a given form. The winning option receives x1 votes, the options one step away receive x2 and x3 votes, or if the winning option is on the edge and there is only one option that is one step away it receives x2+x3 votes, and an option two steps away receives x4 votes, with x1>x2+x3 and x2, x3>x4. For the sake of simplicity, assume that x1, x2, x3, and x4 are large enough relative to the number of vote(s) i has that we can disregard i's term in the sums:

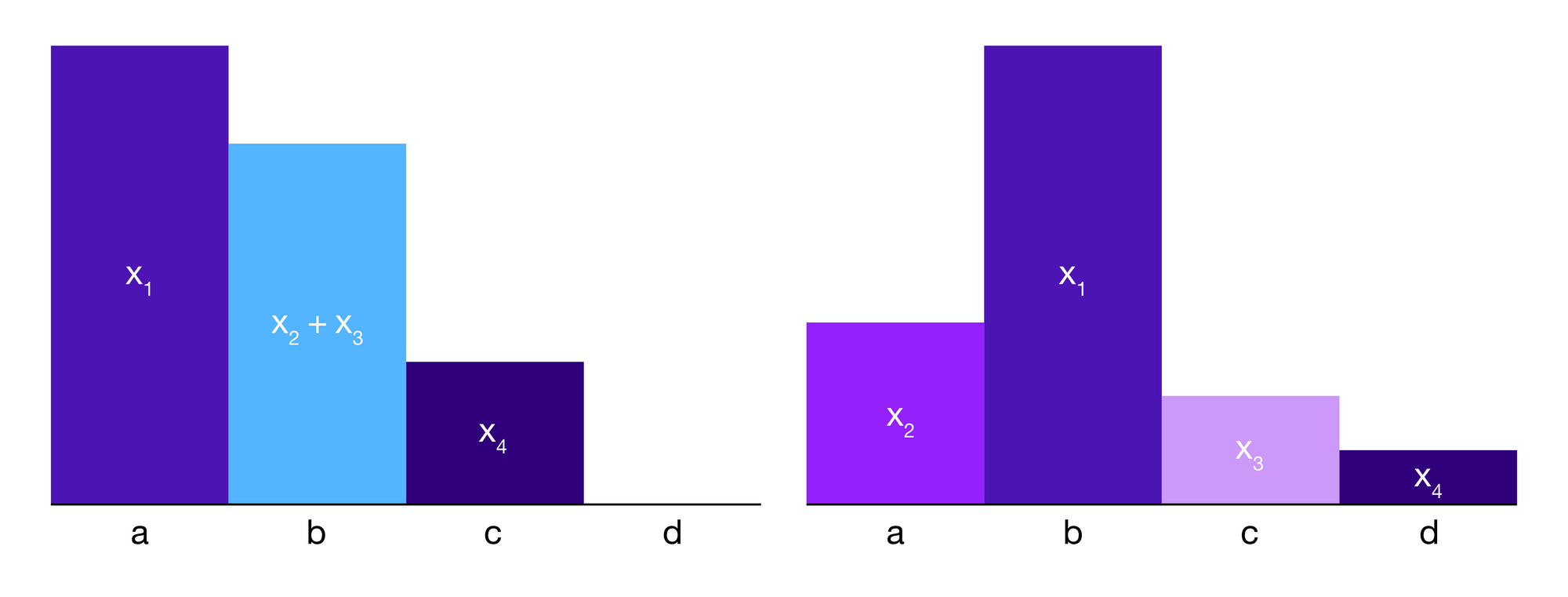
Then, i's expected payoff for honestly voting for a is:
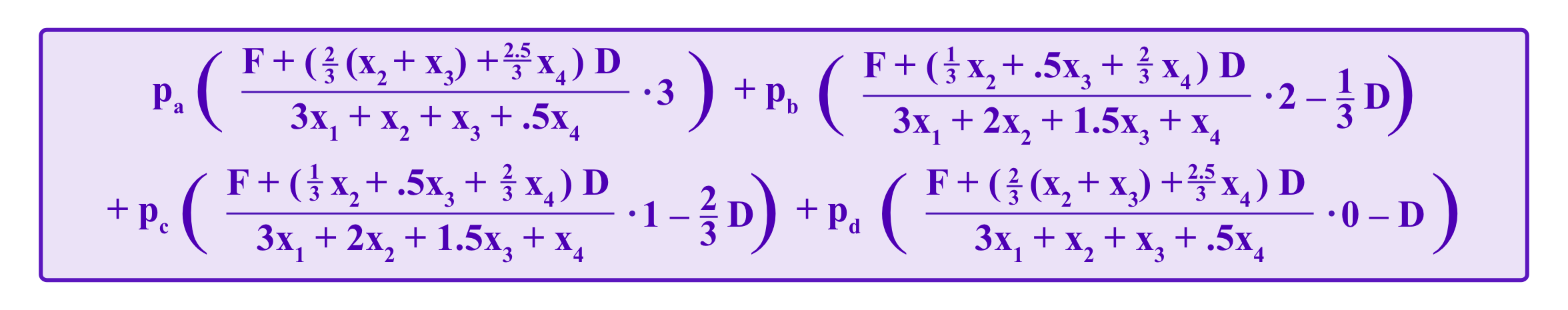
On the other hand, i's expected payoff when deviating towards the center and voting for b is:
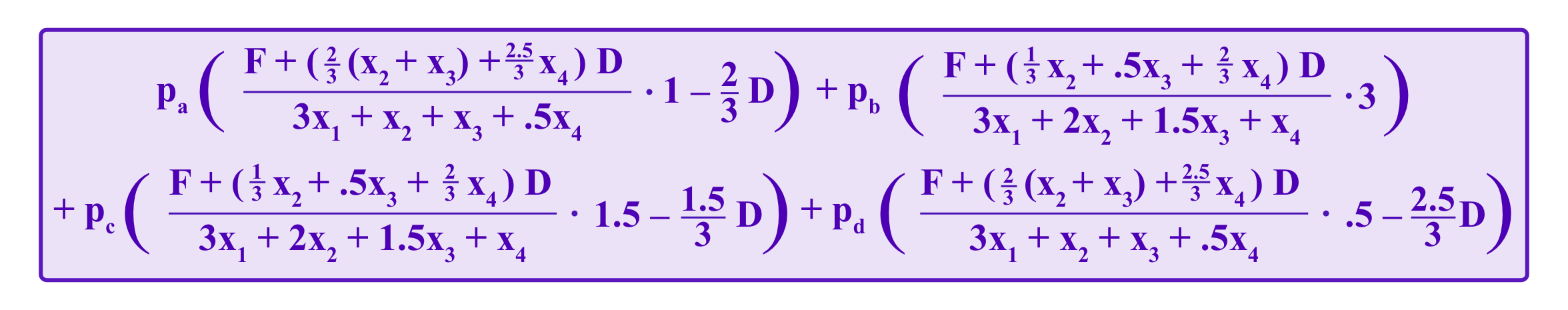
Then, one sees that the expected payoff for voting a is higher than that of voting b using the assumption that pa>pb>pc>pd.
Thus, we see that the choice of f(vi,w) is such that jurors generally aren't incentivized to vote for central options when their honest observation is an extreme option under reasonable assumptions on how the votes of other jurors tend to be distributed. A bias in the incentives that encourages jurors to vote for central options is probably more dangerous than a bias that would push jurors towards extreme options, as it is not hard to imagine a bias towards the central contributing to establishing the central option(s) as rival Schelling-points to the truth.
Nonetheless, one could imagine having parameter(s) that allow one to tune the values in the table we gave above for f(vi,w) so that the expected returns of voting for the outcome the juror believes to be most profitable is incentivized for any position that option might have in the numerical ordering and using the actual historical data of how other jurors' votes are distributed.
Discretizing Payoffs Using Juror-submitted Precisions
Finally, we'll briefly consider another approach to numerical questions based on a paper that I wrote with Clément in the conference proceedings of Tokenomics 2019
At the time the main motivation was to use Kleros in resolving disputes about price oracles, for example, the price of ETH in EUR. The idea was that a new category of actors, called respondents, would provide information about prices. The motivation of respondents was considered to be external; typically they would want price information to be available on some other dapp. Then to the degree that the information provided by the respondents is contradictory, one can resolve these contradictions through a series of binary Kleros disputes where Kleros jurors are asked if the price should be higher or lower than some value.
As those disputes would be binary, they would work well within the framework of the v1 of Kleros that uses Plurality voting. However, as v2 approaches and dispute kits with new voting and incentive systems are possible, one asks if it is possible to modify this approach so that the respondent and juror roles are combined and one doesn't need to assume the existence of externally motivated actors.
A possible approach in this direction is to require each juror i involved in a numerical question to submit three values: li, ai, ui such that li<ai<ui. The idea is that li and ui should be lower and upper bounds on where the juror realistically thinks the value could be, and ai should be her best guess for the value somewhere inside this range.
In some applications, the size of the interval between the values of li and ui that jurors submit will be larger (as a percentage of the values) than in others as some values are intrinsically more uncertain and harder to estimate than others. Even if this system was used for a price oracle for a given pair such as ETH in EUR, there will be times of high volatility when one cannot reasonably estimate the market price with as much precision as one can when the price is stable, and in such situations, it would be natural for jurors to submit larger intervals. Thus, this mechanism allows the jurors themselves to provide information on how much "uncertainty" one expects in the estimation of the value.
Then, the values li, ui are used to determine to what degree the information submitted by the jurors is contradictory. Some jurors may submit larger intervals than others because they view a given value as more variable and less capable of being pinned down to a small interval, but to the degree that the intervals (li,ui) all intersect, the jurors' information about the value itself doesn't conflict.
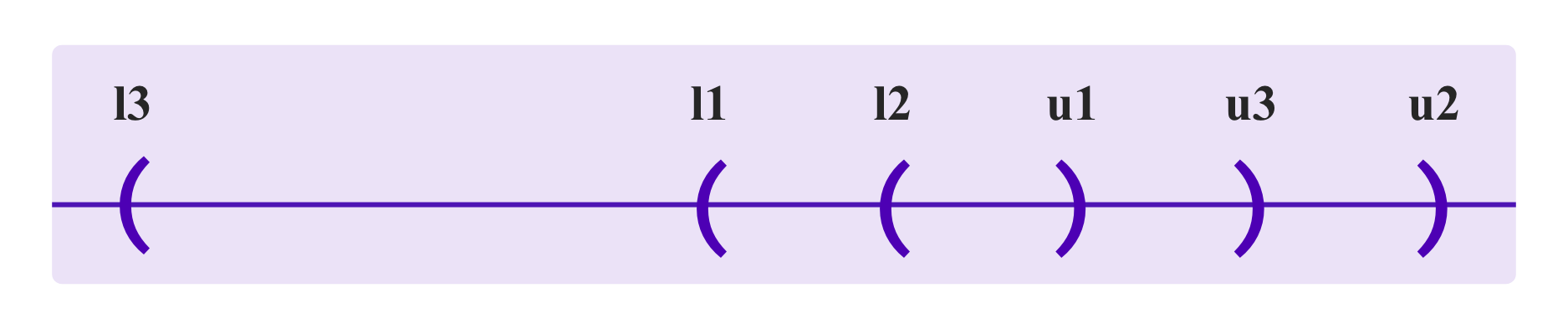
In this case, one takes the output as being halfway between the highest lower bound and the lowest upper bound.
If there are jurors who submit lower bounds that are higher than the upper bounds submitted by other jurors, then the jurors' information conflicts. One takes the set of such points of conflict as:

Then, the values ai are used to simulate how jurors would vote on a dispute over whether the true value is higher or lower than each cj in C0.

The median value of the ai's: am would be the decisive vote on any of these disputes, so we can eliminate lower bounds that are higher than am and upper bound that are lower than am. Then, taking the output value as halfway between the highest remaining lower bound and the lowest remaining upper bound, we have:
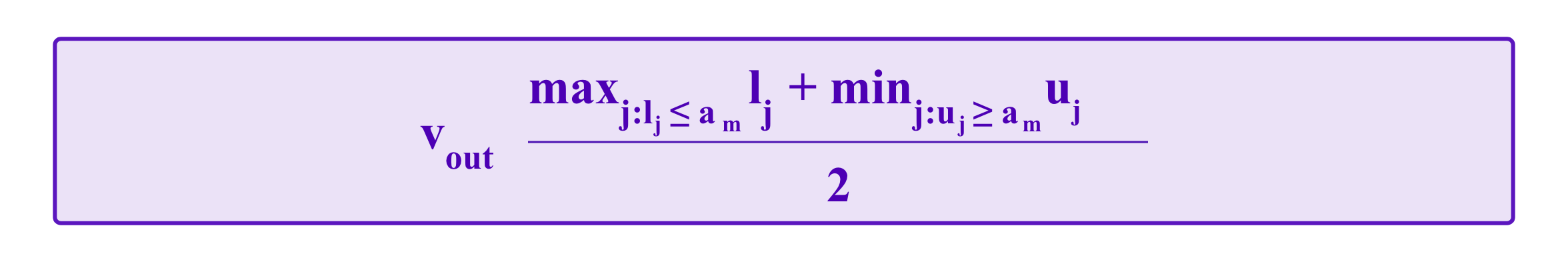
So far, this is still quite median-centric. When calculating the payoffs for the jurors we can take:
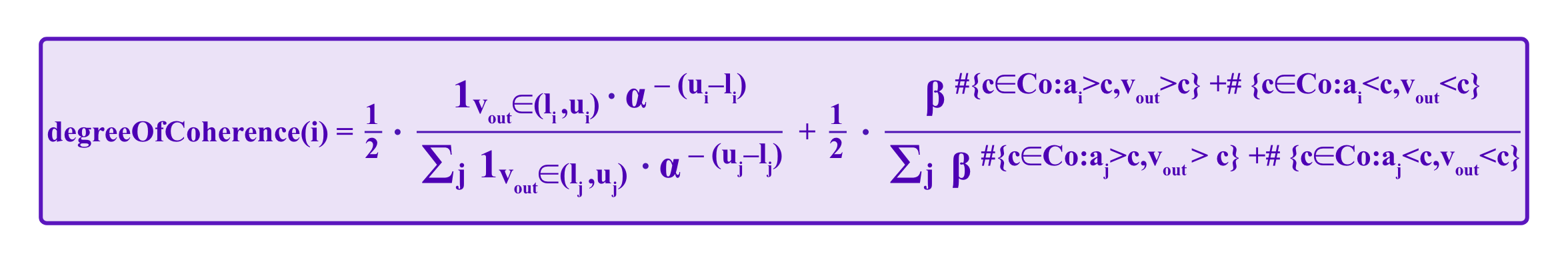
and then the juror i loses

from her deposit of D and gains

in ether and

in redistributed PNK.
The idea here is that in degreeOfCoherence(i), the first term encourages a juror i to submit an interval (li,ui) that is short; the exponential alpha^{-(ui-li)} quickly decays as the length of the interval ui-li grows. However, the juror is also incentivized to not submit an interval that is so short that she risks vout falling outside of it as then she receives a contribution of zero from this term.
The second term rewards a juror whose value of ai is on the same side of a point in C0 as vout for many such points. Namely, the juror is incentivized to submit a value of ai close to the median, where "close" is now in terms of a number of points in C0 rather than the previous measures we had considered (namely, the percentages of voters with closer or further responses, and the number of discrete options between the jurors vote and the median).
Under this system, an attacker cannot cause the output value to leave the interval of agreement between the honest jurors except to the degree that there is a point c in C0 (which potentially the attacker engineers herself by her submissions) where there are enough votes on the "malicious side" of c. So, to the degree that such an attack fails, the attacker will typically have a large number of votes on the opposite side of c from vout and she will be penalized in the second term of the calculation of degreeOfCoherence(i).
Thus, the approach of this system to avoid the types of "micro-cheating" discussed above is to determine how big of a difference in the output value is "meaningful" in terms of the values li and ui that the voters themselves submit, and then to ensure that there is value at stake at the points where slight differences in the user responses could meaningfully change the outcome – namely, on how the user votes on the points in C0.
Conclusion
Over the years, we have worked hard in making the Kleros protocol more flexible to address more use cases. A result of this work is that the upcoming v2 of the Kleros court will have modules for different voting and incentive systems that can be adapted to specific types of disputes. Allowing for disputes whose outcomes are numerical is particularly exciting as this can open the doors for many new use cases in fields such as freelancing, insurance, intellectual property, and content moderation.
We have considered a few different approaches here, with their respective tradeoffs, for how to handle such questions.