Kleros and Social Choice Theory: Research Paths for the Future

What happens if Kleros needs to resolve disputes that have more than two solutions?

Up to this point, the disputes handled by Kleros have largely been binary. Jurors have been presented with options such as "Yes, add this to a list" versus "No, do not add this to a list" or "This is fake news" versus "This is not fake news".

To the degree that jurors have been given more than two options (e.g. strictly speaking jurors also always have the option to vote "Refuse to arbitrate" if the case does not adhere to court policies), the other choices have generally been marginal to the point of de-facto binarizing the dispute.  

However, many potential use cases do not fit into the model of having only two possible outcomes. When parties enter into an economic relationship, agreeing to use Kleros in case of dispute, they need to define the options that eventual jurors would choose between if a dispute ultimately happens. In many cases, they would want to provide jurors the flexibility to decide outcomes that are not as simple as ruling for one side or the other. For example, we could have cases where:

• In a Kleros escrow contract where small business owner Alice has hired freelancer Bob to make her a website, outcomes could include paying Bob, refunding Alice, as well as options to give Bob more time to make improvements to the website.
• In a Kleros based insurance system, when Alice claims a certain value of insurable damages, options could include paying her the full requested amount, rejecting her claim, or paying her some partial amount.
• In Kleros based social media content moderation, when a problematic piece of content is flagged, jurors could have options to maintain the piece of content, to remove the content without deleting the offending user's account, and to remove the content and delete the offending user's account.

In this article, we will review some ideas from social choice theory which influence our design choices as we build Kleros so that it can handle disputes with many outcomes in a secure way.

First Past the Post and Its Problems

Modern elections have taught us that voting can become complicated when there are more than two candidates. Particularly, in the United States and the United Kingdom, there have been several famous elections marked by warnings of "vote splitting" and suggestions of "tactical voting".

Both the United States and the United Kingdom use an electoral system called "First-past-the-post" or, in the language of social choice theorists, Plurality. In this system, voters select a single candidate and the candidate with the single largest number of votes wins (even if no one candidate receives a majority of the votes because there are many candidates). Then:  

• If there are two similar candidates that would appeal to the same group of voters, each of them can be expected to receive fewer voters that they would if the other candidate was not in the race. Then it is possible that neither of them wins even if one of them would have won had the other not been present. This is the concept of "vote splitting". This is what happened in the 1912 US presidential election.
• Suppose a voter thinks that candidate A is great, candidate B is not as good but is acceptable, and candidate C is terrible. If the voter decides to vote for candidate B instead of candidate A because she thinks candidate B is more likely to be able to beat candidate C, she is said to be making a "tactical vote".      

See, for example, the tool created by www.tactical.vote for the recent December 2019 UK election which suggests which tactical vote people should make in order to prevent a Conservative majority government based on where they live.

Borda and Condorcet: Alternative Voting Systems

In the 18^th century, the French philosophers and mathematicians Jean-Charles de Borda and Nicolas de Condorcet realized the issues with Plurality voting and proposed alternative systems.  

• Borda proposed the following system when there are N candidates. Each voter submits a list of as many candidates as she wishes to rank, ranked from her first choice up to the last choice. Her first choice receives N points, her second choice N-1 points, etc. After all votes have been counted, the candidate with the most points wins.

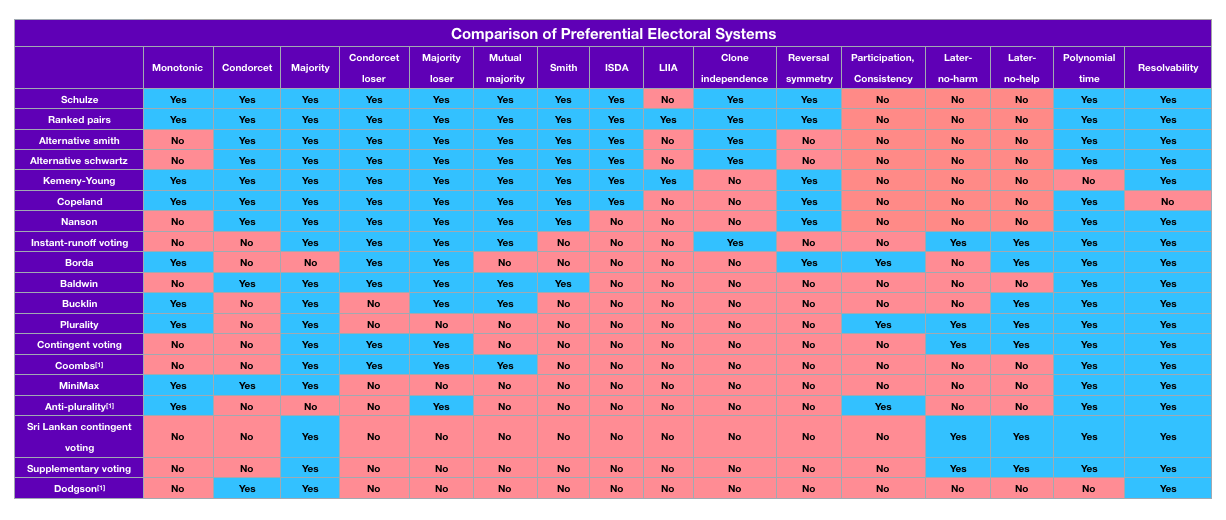
• Condorcet proposed simulating pair-wise election "duels" between every two candidates in an election. For example, if voters rank the candidates from the first to last choice, for each pair of candidates A and B one can check if the majority of voters ranked A higher than B or if the majority ranked B higher than A in their lists. Then if a candidate wins head-to-head against every other candidate that candidate should win the election. However, it is possible that  there is no such candidate; for example, in an election between candidates A, B, and C one can have majorities of voters prefer A to B, B to C, and C to A. This is called a "Condorcet paradox"; as Condorcet did not specify what to do in the event of a Condorcet paradox, this is not considered a voting system in the sense of modern social choice theory. Rather, it is a property a voting system can satisfy; a system is said to be "Condorcet" if it elects a candidate that would win head-to-head against every other whenever there is one. Prominent examples of Condorcet systems include Schulze, Ranked Pairs, Kemeny-Young, Copeland, and Dodgson (invented by Charles Dodgson, better known as Lewis Carroll).

In the ensuing centuries, many other different voting systems have been developed. A notable example is:

• Instant-runoff – Voters submit a list of candidates, ranked in order of preference. The number of first place votes each candidate receives is counted, and whichever candidate receives the fewest first place votes is eliminated. The eliminated candidate's first place votes are reattributed to the candidates whom those voters placed second. One continues in this way, each round eliminating the candidate who is the top remaining choice of the fewest voters until one candidate is the top remaining choice of a majority of the voters. Note that this is equivalent to having a series of runoffs with the number of rounds being one less than the number of candidates.    

Variants of the Borda system are used in the parliamentary elections of Nauru, for the MVP award in Major League Baseball, and for the winner of college football's Heisman Trophy. The Schulze system, a Condorcet method, has been used for board of trustees elections for the Wikimedia Foundation and some internal elections in various chapters of the Pirate Party. The Instant-runoff system is used in Australian parliamentary elections and in the Academy Awards.  

In all of the voting systems discussed above, voters are asked to rank their candidates in order of preference.  

Voting Paradoxes

In 1950, Kenneth Arrow (Nobel Laureate in Economics 1972) showed that any voting system with three or more candidates where voters only submit a ranked list of preferences will have some pathological behaviour, at least in some cases. Specifically, he proved :

So for any ranked-preference voting system that isn't completely trivial (one person deciding) with three or more candidates, there is inevitably a possibility that a "voting paradox" will arise where the votes are translated into results in a way that fails natural properties we would want/hope for a voting system to have.

Gibbard and Satterthwaite built on Arrow's Theorem to show that in any such voting system, there will be situations where a rational voter would vote tactically.

For an example of such a voting paradox in an instant-runoff system, watch the following video:

While Arrow's Theorem tells us that some pathological behaviour is inevitable in any ranked choice voting system, one can nonetheless design voting systems to satisfy some good properties. A few examples that have been considered by social choice theorists are:

• Monotonicity – Suppose that voters cast a set of votes so that the candidate A wins. If some voters had changed their vote to move A up while no other changes are made then A will still win. (One also has a similar condition about moving candidates down not causing them to win.)  
• Clone independence – A set of candidates are considered to be clones if all voters rank them consecutively. Then deleting a clone from every voter's list should not change whether any other candidate outside the set of clones wins or loses.     
• Participation – Suppose that if Charles does not vote, the candidate A wins, and Charles prefers A to B. Then Charles voting should not result in B winning.   

They have found that ranked preference voting systems can have some of the properties but not all one would want.

The good news is that, for many of these voting systems, the paradoxes and failures of good properties only occur on relatively rare edge cases. So one can reasonably hope to pick a voting system that has less problematic tactical voting that Plurality does. Then, the voting system one selects is a question of which 'good' properties one prioritizes.  

Finally, note that other voting systems have also been proposed where voters provide more information than a simple ranking of votes, such as Approval Voting and Range Voting. These systems have a different set of challenges with respect to tactical voting.

Why This Matters for Kleros

The situation of Kleros is somewhat different. Above, we considered elections where voters have some intrinsic preference for which candidate wins. They vote for candidate A because they want A to become president. If, due to some weird voting paradox, voting for candidate B is a more useful vote for the goal of making A president, rational voters would vote for candidate B.  

In Kleros, jurors want to vote in the way that maximizes their economic return. Hence, based on the idea of Schelling points, jurors want to vote with the consensus in order to earn arbitration fees and not lose their stakes. While, jurors as they hold PNK, might have a general desire that Kleros produces honest outcomes so that the system remains credible and PNK does not lose value, we expect this motivation to be secondary as jurors decide to vote on any given case.

Nevertheless, Schelling point based voting has some issues related to the phenomena we saw above. For example, using Plurality for a Schelling point based vote with three or more choices has the following consequences:

• If there are many very similar honest options (or "clones", paralleling the clone independence property considered above), they will divide the votes of jurors that are attempting to vote honestly, decreasing the probability that any one of them wins. Anticipating this effect, jurors might instead vote for a distinguished but dishonest choice. For example, again imagine that we have a small business owner Alice that hires a freelancer Bob to build her a website. If jurors can choose between "refund Alice", "pay Bob" and "give Bob another week to finish the project", they might vote to give Bob more time. However, suppose instead there are several different options that gave Bob another week, another eight days, or another nine days respectively. Then the jurors might avoid all of the "give Bob more time" options expecting the vote to be too split between them for any of them to win.  

• To the degree that no single option is likely to receive more than 50% of the votes, this lowers the bar for the number of votes that attackers need to corrupt to pass a dishonest result. 

As jurors' motivations are economic, considering the incentive system of rewards and penalties is essential to analyzing the voting system. In general, we want a voting and incentive system that:  

• Incentivizes jurors to vote for outcomes they think are correct.
• Aggregates the information provided by the jurors' votes into an outcome that reflect what the group of jurors thinks is correct.

Now, for example, consider the following incentive system for use with ranked choice voting systems. Suppose each juror has a stake of d PNK which represents the maximum she can lose for an incoherent vote. Then suppose that (based on whatever voting system we wind up using) the winning outcome is w. Then, based on her vote, a juror Alice loses:

from her stake, and receives:

ETH in arbitration fees and:

PNK in redistributed stakes. Note that, unlike the binary situation, it is now not necessarily the case that jurors are entirely coherent or entirely incoherent. They can be "partially" right.  

Then one can show :

The perspective of a juror thinking of the ultimate outcome of a dispute being independent of her vote is certainly idealized, but not completely unreasonable for Kleros if jurors expected incorrect decisions to be appealed.  

Now, similar to the tradeoffs in voting system properties that we saw above, when choosing a voting system for a Schelling point based model there are a number of properties that we might want.

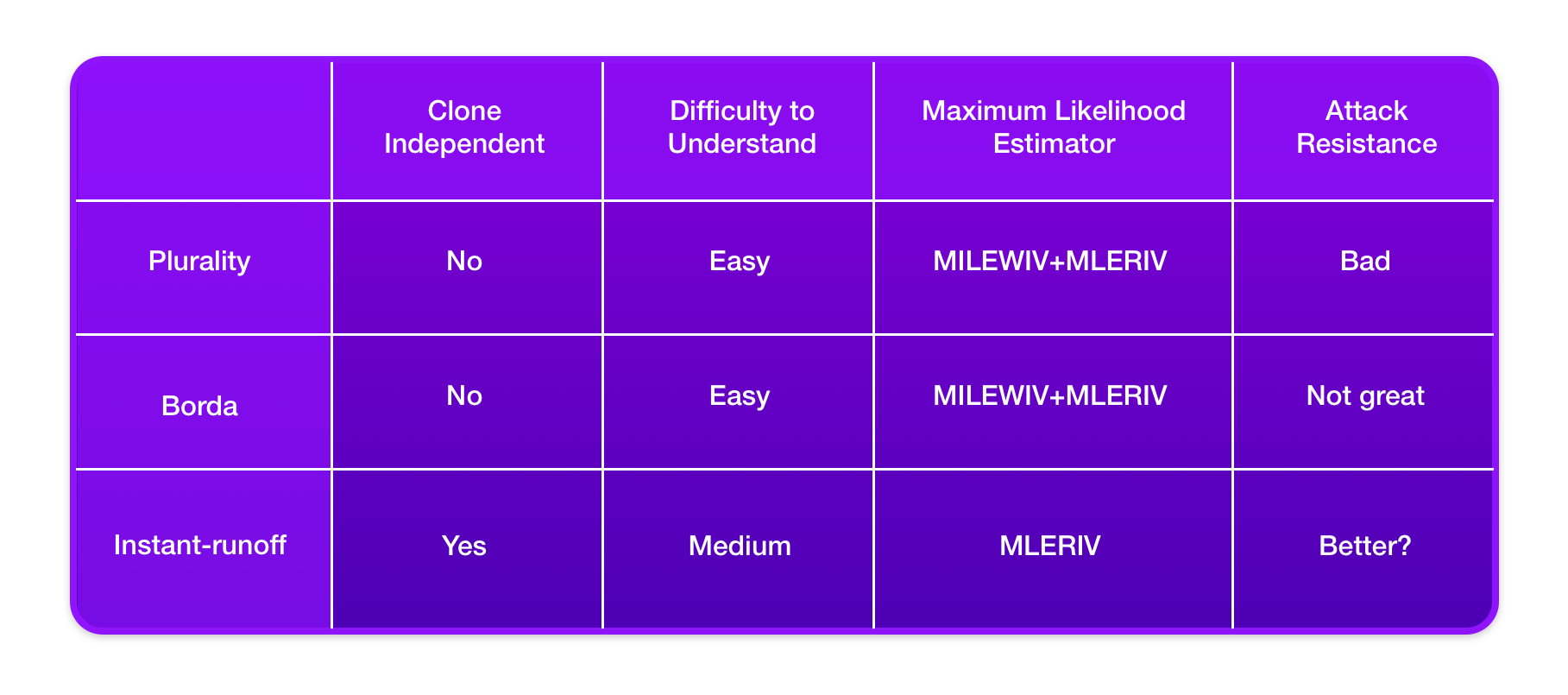
Clone Independence  

The standard property of clone independence that we already looked at above is even more important in the context of Schelling point based voting, as we saw in our criticisms of Schelling point Plurality voting. By choosing a clone independent voting system, parties drafting a contract that designates Kleros as its arbitrator can worry less about whether the choices they include will cause "vote splitting".

Easy to Understand

When a country chooses its leaders via a democratic election, it is important that its citizens understand the voting system so that they can fully engage in the democratic process. However, a Kleros juror may need an even better understanding of the voting system than she is using as she is tasked with mentally simulating how a vote is likely to play out to maximize their chance of being coherent with its output. Hence, it is better to choose a voting system that prospective jurors do not need to spend a lot of effort to understand.

Voting as a Maximum Likelihood Estimator

If the incentive system succeeds in incentivizing jurors to provide their honest opinion of a dispute, one might think of the jurors' votes as indicating the "true outcome" with noise, namely that which outcome(s) jurors think deserve to be ranked high is probabilistic based on some distribution that is conditional on the "true outcome" being a certain option.

This model is similar to the framework considered in work such as that of Conitzer and Sandholm. They study which voting systems can be thought of as maximum likelihood estimators when the jurors vote distributions are independent and identically distributed; namely, which voting systems return the outcome that is most likely to be the "true outcome" given the noisy votes and assuming a uniform prior over the outcomes.

This is a good measure of whether the voting system is doing a good job of transforming the "noisy signal" of the jurors' votes into correct outcomes.

Conitzer and Sandholm consider two points of view; they say a voting system is MLEWIV if it is a maximum likelihood estimator when the "honest" answer is thought of as being a single outcome, and MLERIV if it is a maximum likelihood estimator when the "honest" answer is thought of as being a full ranking of the possible outcomes. While it may be that in some Kleros cases one can think of there being an "honest ranking" of all options, the MLEWIV model is more relevant for Kleros.  

Attack Resistance

Possibly the most important property for a voting system on a blockchain, a world in which for example one can have smart contract enforced bribes, is that it be resistant to attacks. This is essentially economic.

We want the number of votes that would need to be changed to result in a "dishonest" outcome winning to be high, with the rationale that this increases the cost of attacks, such as bribes that would be necessary to change those votes.

We already discussed reasons why Plurality is not as attack resistant as one would want in Schelling point based systems. For another example, in the Borda system, an attacker that wants B to win where A is the "honest answer" can perform a "burying attack" where a relatively small number of attacker controlled votes put B first and A last.

In contrast, in instant-runoff a successful attack requires that in at least one of the "runoffs" that B receives more votes than A, which should require corrupting a much larger percentage of the jurors. (Note: with the incentive system described above, the total economic cost in lost deposits if these two attacks narrowly fails are actually comparable; just the attack on instant-runoff requires that a large number of jurors lose a small amount, whereas in the attack on Borda a small number of jurors lose a lot. We have a version of the above incentive system that weights based on which outcomes are "narrowly defeated" and under that incentive system instant-runoff seems to perform better than Borda according to the measure of lost deposits for narrowly failed attacks.)

We have summarized how different voting systems fare on some of these properties in the above table.

Note: It can be difficult to prove that there exists no attack on a given system, so we use a question mark to indicate systems that seem to be more attack resistant based on current research.

Conclusion

We have been using Plurality voting for Kleros, which has worked well because the disputes we have considered so far generally were de-facto binary, namely they only had two plausible outcomes. As Kleros addresses more complex, non-binary disputes we want a voting and incentive system that handles well some of the challenges that that presents.

As social choice theory has seen for standard elections, this involves accepting tradeoffs. Instant-runoff voting with a (weighted) version of the incentive system that we present above is a promising choice, but we will continue to research these questions.

Where Can I Find Out More?

Join the community chat on Telegram.

Visit our website.

Follow us on Twitter.

Join our Slack for developer conversations.

Contribute on Github.

Download our Book