Parameterization for Kleros courts

When creating a new Kleros court, or updating an existing court, a number of parameters have to be chosen.

TL;DR

One can use a variety of heuristics to generate the different parameters that are appropriate for a court. For some of these parameters, one can use a Colaboratory sheet to find parameters that satisfy constraints related to attack resistance. The following checklist summarizes the points one should consider, which we will delve into in the rest of the article.

Checklist

• Choose name and parent court

• Write court policy

• Estimate typical effort required to evaluate cases

• Estimate degree of subjectivity.

• How often will jurors who make honest effort agree with community consensus?
• How often will jurors who don't make effort be able to guess community consensus?

• Run Colaboratory calculator to find feeForJuror, minStake, and alpha

• Imagine dynamics around appeals
• Do you expect third-party crowdfunders to be engaged in funding these cases?
• If appeal to parent court will jurors there more or less have skills to conduct independent review?
• If expect appeals to be robust, can take hiddenVotes=0. Otherwise, may want hiddenVotes=1.
• If appeals to parent court are not problematic, probably want to start new court with small jurorsForCourtJump, e.g. 15.
• Choose period lengths that give enough time but don't cause unnecessary delays

Finally, candidate sets of parameters are proposed in forum posts such as this :

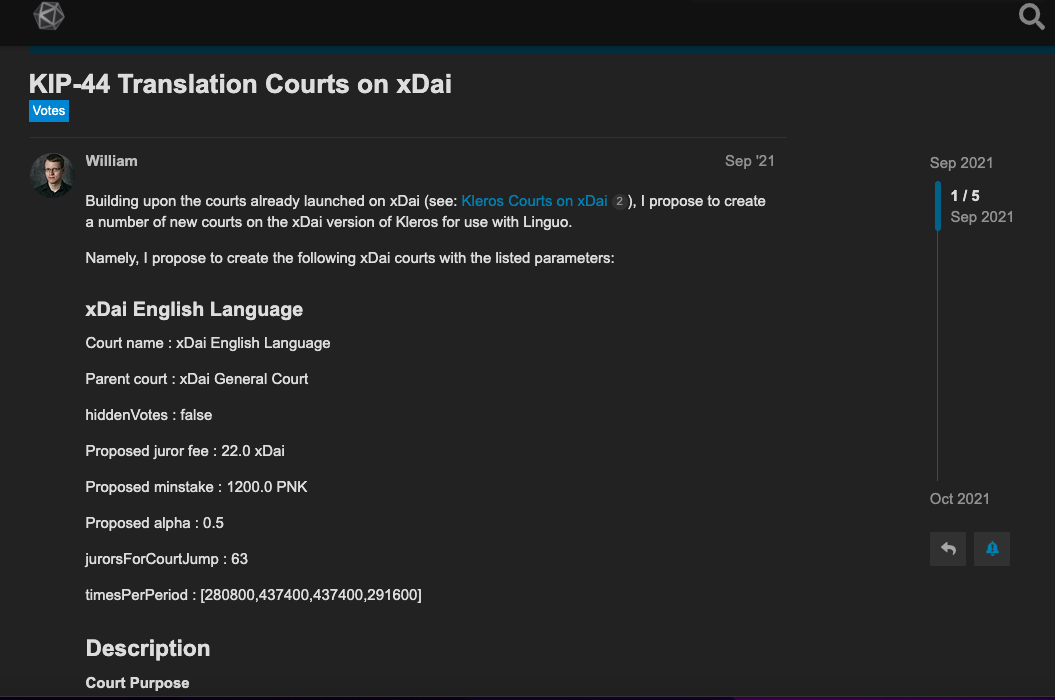
Then the community decides whether or not to adopt these proposals via a governance process that uses Snapshot and the Kleros Governor.

As one can see, there are several parameters that one must consider for each court that determine different aspects of its behaviour. In the rest of this article, we will walk through some of the ideas that one should keep in mind when making each of these choices.

Court name, Parent court, and policy

If you are creating a new court, you will need to give it a name and write its initial policy. These choices essentially define the role of the court in the Kleros ecosystem, determining what types of disputes should be resolved there and determining the requirements on jurors to stake there.

Writing a good policy can be quite subtle. One should anticipate ambiguous situations that might arise in cases and give jurors guidance on how to consider them. Generally, it is essential that jurors have clear instructions on how to handle the cases in the court. See this guide for some thoughts on writing policies for Kleros courts.

Another important choice is what the "parent court" of your court should be. Kleros courts are organized into a tree with each court having a single "parent". If a case is appealed some sufficient number of times in a given court, the case can be elevated to be considered instead by the parent of that court. Eventually, cases can be appealed all the way to the General Court, which is the root of the tree and serves as the ultimate appeal court for all other courts. Jurors staked in a given court are also staked in the parent of that court. Hence, all jurors staked in any court are staked in the General Court.

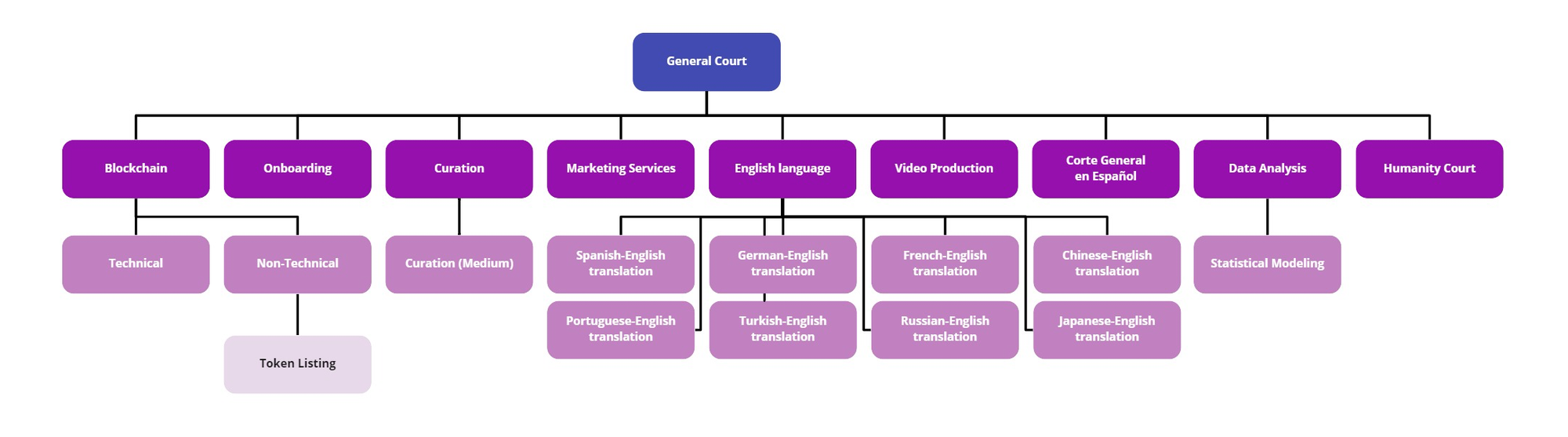
Typically, the parent of a court will have a somewhat broader focus and have less requirements on its jurors than the child court. This allows the parent court to capture a broader swath of the Kleros community, making it more resistant to certain attacks such as 51% attacks and bribe attacks.

While this increased attack resistance comes at the expense of somewhat reduced specialization and expertise, the children court of a given parent should have still requirements that are sufficiently related to that that of the parent court that jurors in the parent court are still likely to have a basis on which to judge the arguments and juror justifications that were made in the child court. Thus, the choice of parent court also relates to what type of disputes a court resolves and its place in the broader Kleros ecosystem.

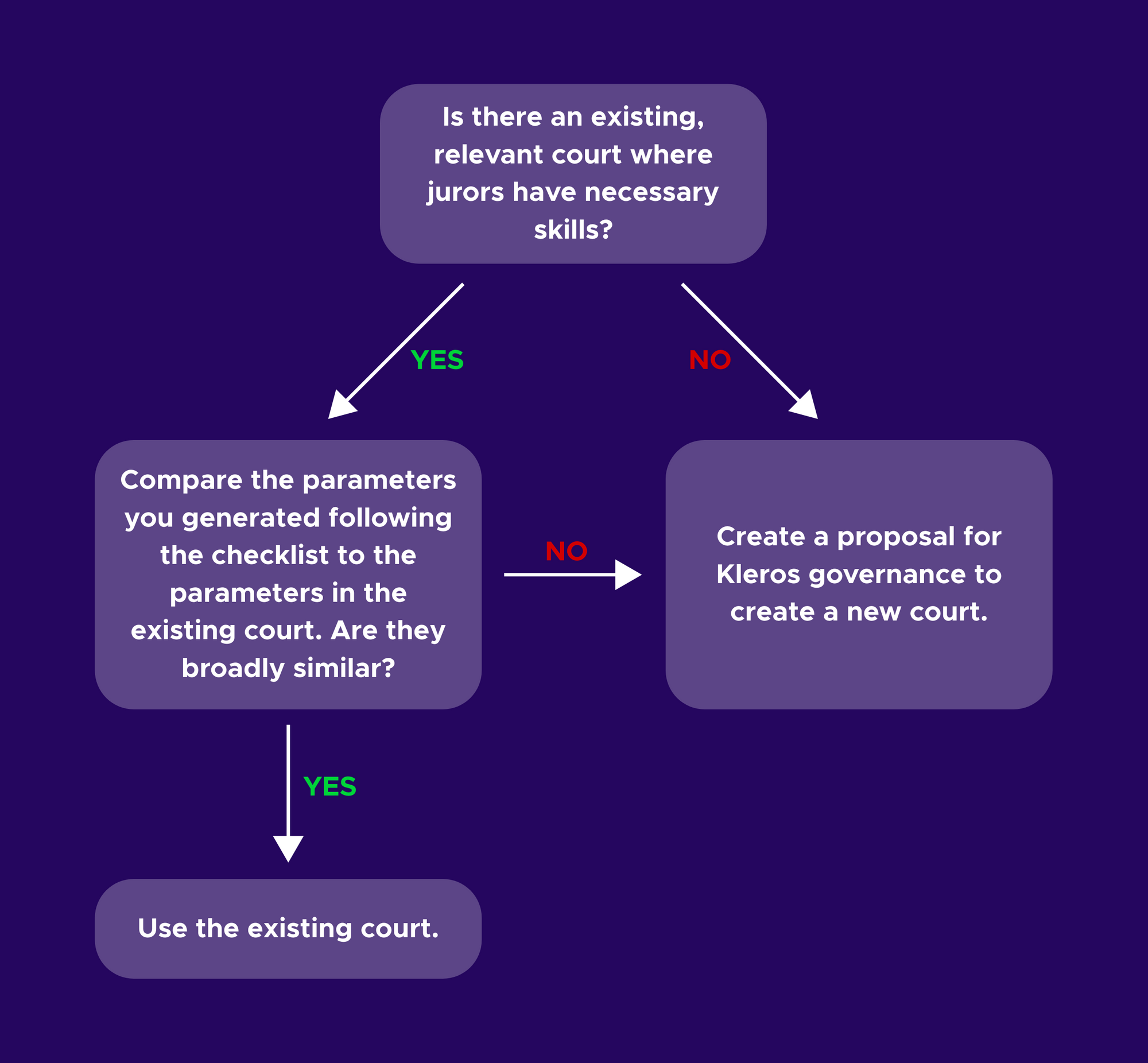
At this point it can be helpful to take a step back and ask yourself whether you actually need to propose a new court. If you are creating a new court, you might think about whether the role you have in mind for that court is already being fulfilled by some existing court in the Kleros ecosystem. Presumably you have some category of disputes in mind that you think Kleros can solve.

You might think about whether these disputes fit naturally into any of the existing courts. For example, if you have a dispute that involves jurors judging whether Solidity smart contracts have bugs, maybe the Blockchain Technical Court on mainnet is appropriate for your dispute as it already requires jurors to have those skills. If you have cases that consist of unskilled microtasks in content moderation, maybe the GnosisChain Curation court is appropriate for your usecases. If you make use of an existing court, there will already be jurors staked in the court when you launch which can lead to a smoother launch than creating a new court and having to bootstrap a community of jurors to stake in it.

However, even if a court exists that deals with broadly similar disputes to yours already exists, that court's values for the other parameters that we will consider below may not be appropriate for your dispute. Notably, the existing court may not be calibrated for tasks at the appropriate scale of difficulty.

For example, the various translation courts (Spanish-English Translation, French-English Translation, Chinese-English Translation, etc) require high knowledge of the two relevant languages and an ability to judge the quality of translations between them. The current implementation of these courts are calibrated for tasks where the jurors might spend roughly half an hour looking at several exerts from a long text and judging whether word choice is appropriate to context and, in some cases, whether the style of a text is consistent. If one only needs to have jurors review translations of a few hundred words, such as if the texts are being drawn from Twitter, then the amounts paid to the jurors using one of the existing courts might be excessive and cost-prohibitive. Instead you might consider creating a new court such as “Spanish-English Translation (Microtasks)“  and setting it as a child court of the existing Spanish-English Translation Court.

feeForJuror, minStake, and alpha

Once a court's basic role has been determined by setting its name, parent court, and policy, another fundamental set of choices are those that determine how much coherent jurors are rewarded and how much incoherent jurors are penalized. These amounts should correspond to the scale and difficulty of the tasks in the court. For example, a court that handles content moderation micro-disputes would generally have lower fees and deposits than a court that requires jurors to verify whether Solidity smart contract contained any bugs to decide if smart contract insurance policies should pay out.

There are three variables in the current Kleros contract that govern these amounts: feeForJuror, minStake, and alpha.

The feeForJuror determines the amount that a coherent juror earns. Specifically, in order for a dispute to be raised or for an appeal to be triggered with n jurors, an amount of feeForJuror*n must be paid to the contract. Then this total amount of feeForJuror*n is split among the coherent jurors. So, if all jurors in a given voting round are coherent, they are all paid an amount of feeForJuror, though if some jurors are incoherent or do not vote the amount the coherent jurors receive can correspondingly be somewhat higher. This amount is denominated in ETH on Ethereum mainnet and in xDAI on Gnosis Chain.

One potential imaginable approach would be to have every juror select for herself what feeForJuror she was willing to accept in a given court/for a given type of task. Then, a given arbitrable application that uses Kleros can set a threshold price it is willing to pay per juror, and the jurors for a case involving that application are drawn from among the jurors whose declared fee is no greater than the threshold.

This is a natural, free market type idea and using this approach would mean that this parameter would not need to be set by Kleros governance at all. However, this idea presents some potential problems. An attacker that knows a case in which she has an intrinsic interest is upcoming can set the fee that she is willing to accept to be very low. If the arbitrable application sets its threshold too low, this will result in the attacker being drawn with disproportionate weight.

This places a lot of responsability on the users of the arbitrable application to set an appropriate threshold that includes a wide swath of the community. Arbitrable application users that think they are setting a price to drive a hard bargain with Kleros jurors may, in fact, be undermining their security. Thus, under this approach, users of arbitrable application would need to have a subtle understanding of the internal dynamics of Kleros, whereas ideally arbitrable applications can plug Kleros into their systems without having to overly think about how it works.

So, instead, feeForJuror, along with the other Kleros parameters, is set by a vote of Kleros governance. In order for an attacker to vote through a malicious set of parameters, she would need to have more than half of the PNK that participated in that vote. Thus, this is similar to the attack model of the Kleros court itself whose security is designed around the assumption that 51% attacks should be difficult.

The minStake is the minimum value of PNK that must be staked in order for a juror to stake in a given court. However, depending on the court, the amount that a juror is penalized for an incoherent vote may be less than minStake. This is essentially due to the tree structure of Kleros courts. As discussed above, jurors staked in a court are also automatically staked in its appeal court which is the "parent" of that court in the tree. Then, the values of minStake must be such that if a juror stakes the minimum amount of PNK to stake in a court, she should also have staked enough to stake in the various parent courts up to the General Court that she is automatically also staked in. Namely, one should have :

minStake(court)>=minStake(parent of court)

for all courts. However, the requirements that we will discuss below  on how much an incoherent juror should lose will not necessarily require that incoherent jurors in a court actually lose at least as much as incoherent jurors in the parent of that court. So we also have the parameter alpha, and we set the penalty for incoherence as:

voteStake=minStake*alpha

Then we have the freedom to calibrate incoherence penalties on a court by court basis; if a court needs to have a high minStake to accommodate the minStake values in its child courts but doesn't actually require that large of a minStake for its own cases, that court can be set with a correspondingly low alpha.

Estimating inputs to parameter calculations : subjective estimations

In order to determine feeForJuror, minStake, and alpha, we can make use of a Colaboratory sheet. This tool requires a number of estimations as inputs. Some estimations are subjective and can best be made by jurors who are handling the corresponding cases. Indeed, these are the people who are best placed to propose parameter updates in those courts. For example, one needs to estimate :

1) An estimation e of the typical amount of effort exerted to evaluate the case. In the calculator, this value should be represented in some (preferably relatively stable) base unit such as EUR or DAI.

2) An estimation p of the probability that a juror who makes the effort e with come to the same conclusion as the honest consensus opinion of the community.

3) An estimation t of the probability that a juror can come to the same conclusion as the honest consensus opinion of the community without making an effort to evaluate the case, such as by voting randomly or always voting according to a fixed pattern.

For proposing updates to existing courts, estimates for p and t can potentially be drawn from historical data. For example, one can calculate the average rate at which jurors have been ruled coherent in different courts. If one takes the point of view that jurors are mostly making an honest effort to review cases, this rate of coherence serves as a reasonable approximation of the probability that a typical honest juror will agree with the consensus opinion on the case. This data is provided in the following tables for the Blockchain Non-technical Court and the Blockchain Technical Court:

Data through dispute number 1316:

We see that both of these courts have average coherence rates around 90%, so p=.9 is a reasonable approximation in these courts.

A lower bound for t in cases where jurors decide between two alternatives is 50%, as a juror can always vote randomly and have a 50% chance of successfully choosing the alternative that reflects the consensus of the community. However, there are also other strategies that a dishonest participant could employ to rule on cases. For example, if most cases in a given court involve ruling on whether an item satisfies the criteria to be included in a curated list, one can look at the historical rates that cases have been decided for “accept” versus how many have been decided for “reject”.

In the following table we have this data for the Blockchain Non-technical Court, where most of the cases up to this point have considered whether tokens satisfy the criteria of the Tokens Registry.

Data through dispute number 1316:

We see that roughly 70% of these cases are ruled “Reject”. Thus, if a dishonest juror wants to employ a strategy that doesn't require analyzing individual cases, always voting to “reject” on cases in this court will have a higher rate of success than a strategy of voting randomly.

So one might estimate t=.7 for this court; however, note that there could exist more sophisticated strategies that an attacker might employ to improve her chances of being coherent while nonetheless not contributing the time and effort to analyze individual cases. If further research identifies such a strategy for some court, one might want to adjust t accordingly.

We will see below that the Colaboratory calculator tries to make sure that such “lazy” strategies have negative expected returns.  Voting strategies that do not consider the facts of individual cases could become particularly problematic if they are sufficiently likely to be profitable that an attacker would have an incentive to create a bot which executes them automatically. On the other hand, if someone uses an automated strategy that does take into account the facts of cases such as by feeding the evidence and arguments in that case to an AI, it is not as clear that that is a problem.

Conceivably, one could imagine AI jurors participating alongside human jurors in some courts, with both groups giving useful evaluations of the appropriate outcomes of the dispute. Perhaps the typical juror in such a court will be a human being that has access to an AI to help her in her decision making process, but that will ultimately make a final ruling on the case herself.

Note that we have taken a relatively simplistic model of jurors' chances of agreeing with the community consensus on a case as a function of their effort. Either the juror makes an effort of e and has a chance of p, or the juror makes an effort of 0 and has a chance of t.

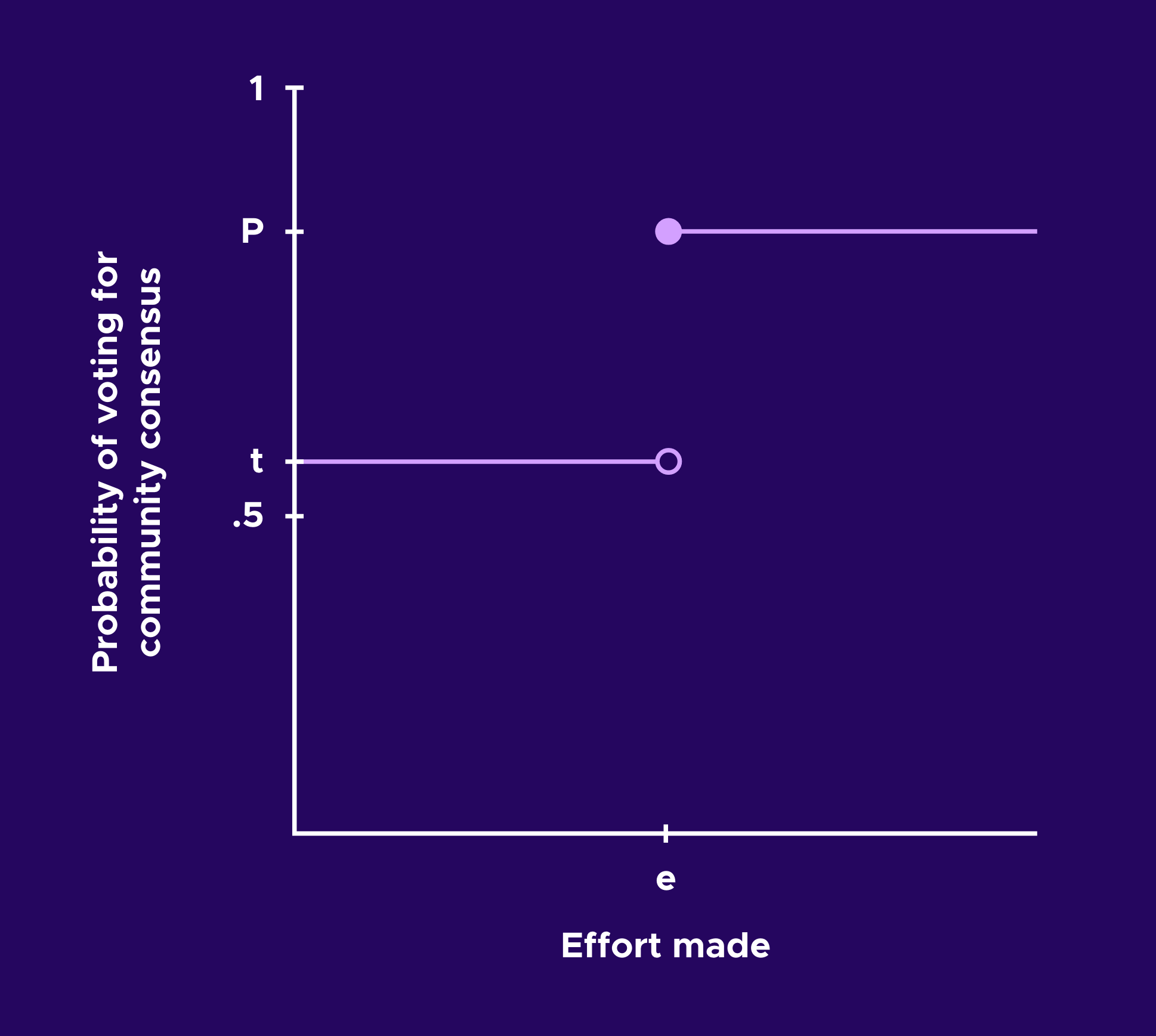
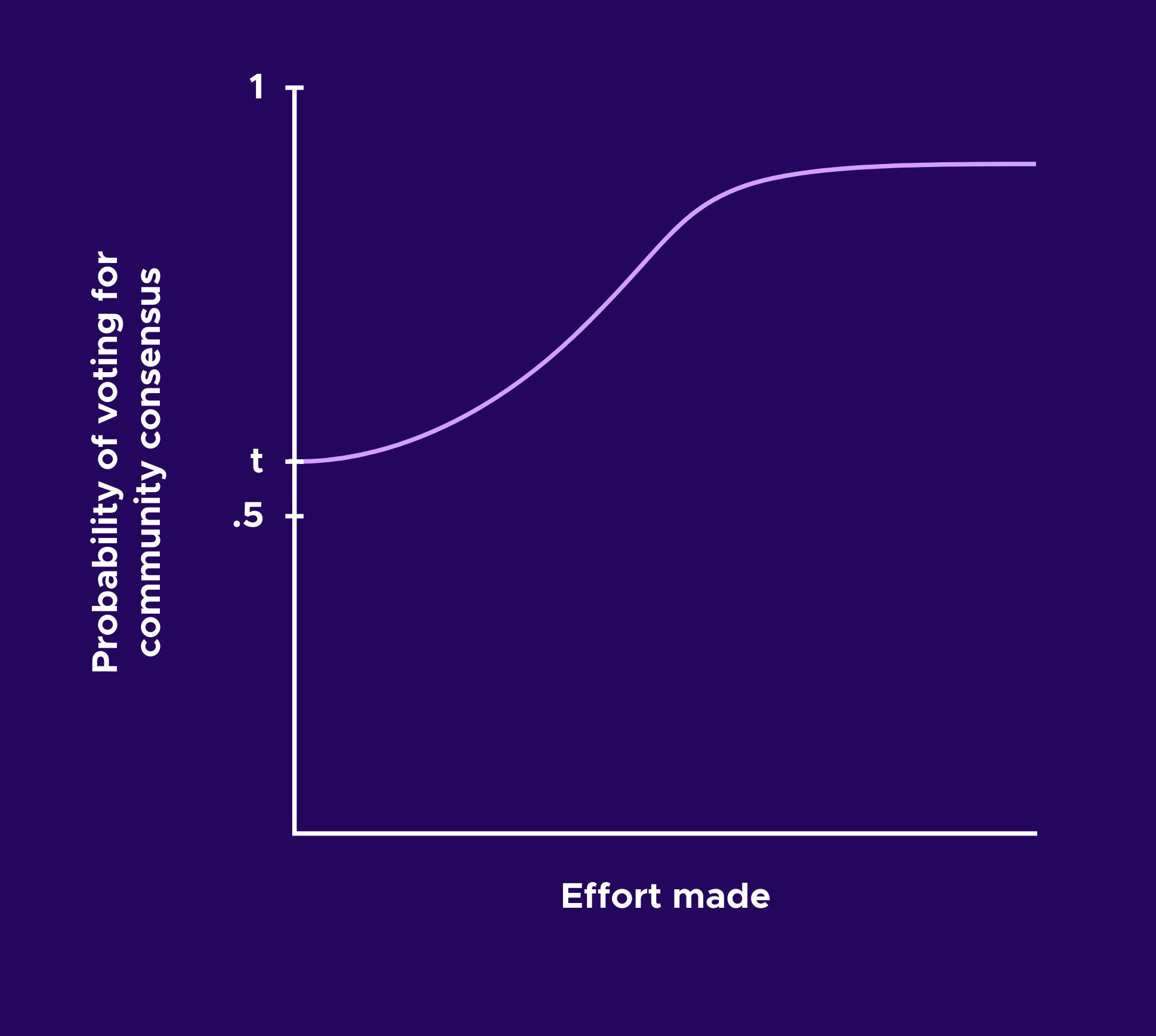
With relatively little case data it is difficult to calibrate a richer model than this. However, if the jurors in a court want to make more nuanced estimates of their chances of agreeing with the community at different levels of effort spent reviewing a case, this data could be potentially used in more realistic models such as those considered in this article.

We don't have any particularly good way of drawing estimates for e, the typical juror effort in analyzing a case, from past court data. So it is particularly important when estimating this value to obtain feedback from the jurors in a given court who are exerting this effort.

Subjective estimates in an entirely new court

If you are trying to set the parameters for a brand new court, you can't survey past jurors to get their estimations for the effort they had to make, and even the historical data that we use to approximate p and t above is not available. In this case, often the best one can do is to imagine some hypothetical disputes in the future court and just make intuitive estimates of how difficult they are and how reliably you feel a juror would agree with the broader community.

Sometimes in the complete absence of good estimates for the level of subjectivity of a new category of disputes, our starting prior has been to estimate p=.85 and t=.6 as these have been broad averages of the types of calculations we have done above over a variety of courts and different types of disputes. Then, one might adjust the estimates up or down somewhat if the tasks that will be in the court seem more or less subjective. However, one may soon realize as new data becomes available that whatever estimate you made was inappropriate, so it is important to be willing to propose further parameter updates going forward.

Estimating inputs to parameter calculations : other estimations required

There are other estimates that are required that are less specific to a given court, but that are variable and need to be updated when computing parameter updates. For example, the Colaboratory calculator requires estimates projecting Ethereum gas prices during the period where one wants to use these parameters. Specifically, the current version of the calculator models variability in Ethereum gas by asking for three values :

1) gasPriceLow – this should be the lowest realistic gas price that one would expect during the lifetime of the set of parameters.

2) gasPriceHigh – this should be a conservative estimation for a relatively high gas price that someone would have to pay over the lifetime of the set of parameters.

3) gasPriceMax –   this should be a very conservative estimate of an extreme gas price during the lifetime of the set of parameters. Ideally, one should be very confident that someone issuing a transaction with this gas price should be able to have their transaction included within the period that jurors have to vote even in the most extreme gas conditions that will occur during the lifetime of the set of parameters.

Below, when we are discussing the various constraints that the parameters we generate will be chosen to satisfy, we will see that feeForJuror will be chosen to always at least cover the cost of gas even at gas prices up to gasPriceMax. Other constraints that will be imposed on the parameters will ensure that participants are appropriately incentivized up to gas prices of gasPriceHigh. One can base these gas price estimates on historical data drawn from sites such as Etherscan, or if one wants more precise information one can find how much jurors have actually been spending on gas when they vote via Dune queries.

Additionally, the calculator requires the values of PNK in terms of ETH and ETH in terms of the (relatively stable) base unit used in the accounting of the estimates of juror effort. These amounts will also vary over the lifetime of the parameters; variability here is measured in how large of a percent change one could expect during this period. While cryptomarkets are unpredictable, one can at least use historical data to get a sense of historical variability for these variability estimations.

The calculator also takes in a few other inputs that are either fixed or at least that one would expect to only slowly evolve over time. These include the number of gas required to vote in a typical case in each court and the number of gas required to appeal typical cases in each court. The number of gas required to vote or to appeal do not generally vary too much from one Kleros application to another, so if you are creating a new court you can probably copy the values used by other typical applications unless your preliminary testing of your application gives you some particular reason to expect to need more bespoke values.

Constraints that parameters should satisfy

The calculator takes the inputs discussed above and attempts to find parameters that simultaneously satisfy several different constraints.

Honest participation should be profitable

A key constraint that one wants the parameters to have is, of course, that the fees and rewards that an honest juror who make an effort to review a Kleros case will, on average, at least compensate her for the effort she makes.

Recall that if a juror's vote is coherent with the collective decision of the last voting round, she receives:

and if she is incoherent with the decision of the last voting round, she is penalized voteStake.

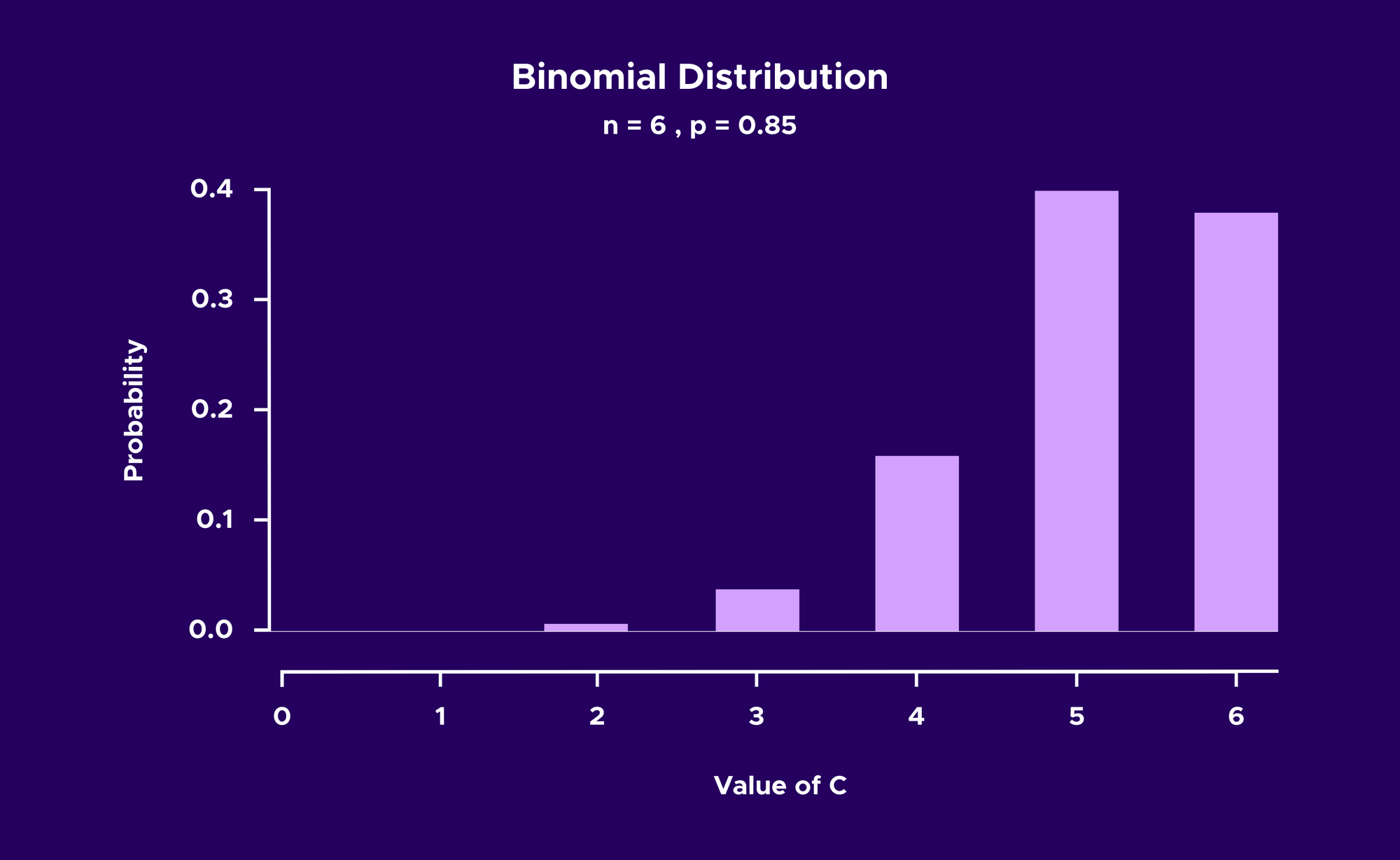
Then in order to calculate the average payout of an honest juror, we need to get a sense of how the number of coherent and incoherent jurors will vary. Suppose that Alice is one of M jurors participating in a voting round. If we think of each of the M-1 jurors other than Alice as independently voting on the case and having a probability of p of voting for the community consensus alternative, then we can define C to be the number of jurors (other than Alice) who will vote for this outcome and model C with a binomial distribution.

Then, Alice's average payoff for being honest is:

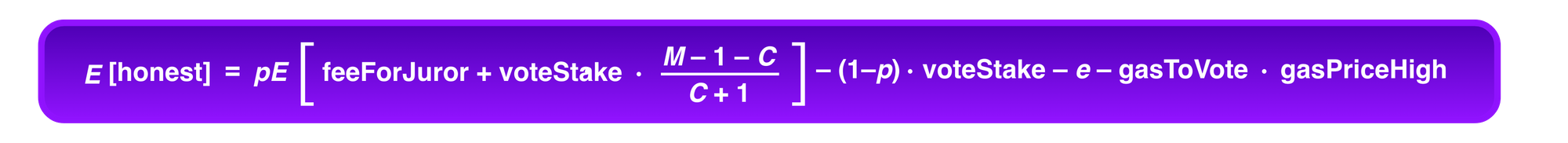
Using standard results to calculate the expected values of functions of binomial variables, this gives:

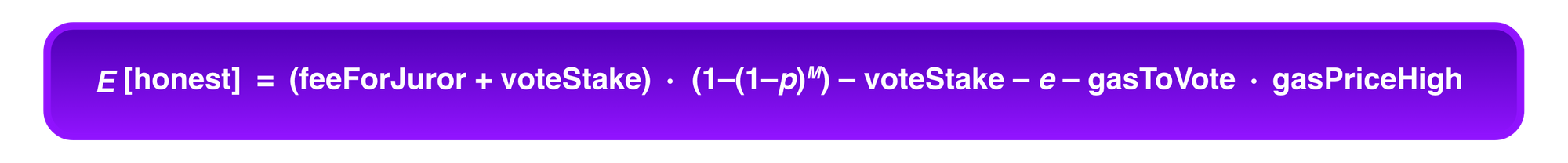
Then, parameters should be chosen so that this quantity is positive.

Voting without making an effort to analyze a case should be unprofitable

Similarly, a juror Eve who does not make the effort e necessary to review a Kleros case should, on average lose money. We can follow a logic similar to above, noting that the “lazy juror” now has a probability of t of choosing the alternative that will win the dispute while the other jurors still have a probability of p of choosing this alternative, so the number of coherent jurors (excluding the Eve) follows the same distribution as C above. Then,

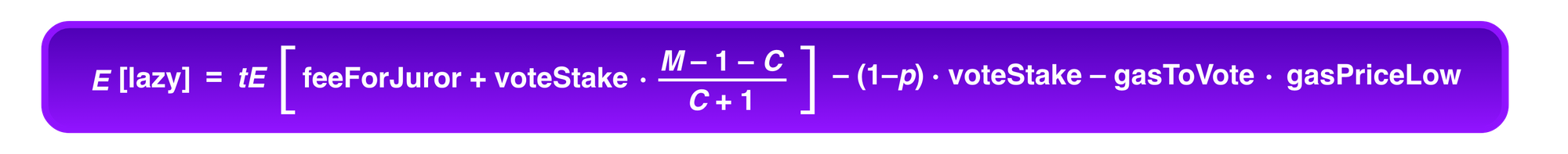
Again, using standard results to calculate the expected value, we can compute:

Then, parameters should be chosen so that this quantity is negative.

Reward for a correct vote should cover gas costs even if there is an extreme spike in gas prices
We want to ensure that even under the most pessimistic, realistic hypothesis for increases in gas fees between parameter updates, that the average fee paid to jurors are at least equal to the gas required for the juror to have her vote transaction included during the voting period. Namely, we want to choose parameters so that :

feeForJuror>gasToVote*gasPriceMax

Resistance to the “Arbitrator-Arbitrable Split Attack”

Finally, we have a constraint that attempts to deal with some situations where jurors vote for an alternative y, and then during the crowdfunding stage only the alternative x is funded. In most applications that use Kleros this means that x is seen by the alternative as having won the dispute, but no appeal round is triggered.

On the other hand, the Kleros court contract sees the alternative that wins the last round of juror voting as having won for purposes of rewarding and penalizing jurors. So in particular, in this situation, a juror that voted for x will be seen as incoherent even though x is seen by the arbitrable application as having won and indeed the reason that no additional appeal round occurred may have been that crowdfunders didn't find the other alternative(s) credible enough compared to x to be worth funding.

The reason that the Kleros court contract sees the alternative that wins the last round vote as the winner rather that the alternative that wins under crowdfunding is that under the arbitration standard that Kleros implements, ERC-792, different applications can handle how they raise funds for appeals in different ways. Some can use crowdfunding mechanisms, but others could for example require the losing side of a vote round to always pay appeal fees or potentially use some other kind of logic.

As any contract can call Kleros and ask for the answer to some dispute, the Kleros contract cannot assume that the application contracts are honest, so it doesn't trust the mechanisms they use to determine a winner of a dispute after not only the Kleros rulings, but also information about appeal funding to be appropriate. Then the Kleros contract only has access to its own internal information, namely the results of the various voting rounds, to determine which jurors to reward or penalize.

Situations where the last round juror vote and the winning alternative as seen by an arbitrable application disagree, while not ideally, are normally not too problematic. While these situations are fairly rare, an honest juror that is penalized in some cases because she voted with a winning alternative that didn't win the last voting round can expect to have this penalty more or less cancelled out in the long run by rewards in other cases where the reverse situation occurs.

However, we have identified scenarios under which this disparity could potentially be exploited by an attacker. We call this the “Arbitrator-Arbitrable Split Attack.” Then the calculator imposes a constraint so that this attack should not be profitable.

Specifically, in a round with M votes, suppose that honest participants control K votes and an attacker but that an attacker controls more than half of the votes in that round by random chance even though the attacker does not posses 51% of the total token pool and would lose in appeal. Namely, suppose the attacker controls M-K votes, where M-K>M/2. Suppose that there is a relatively clearcut honest answer of x and y is a dishonest answer. Then the attacker, uses her M-K votes to vote for y and immediately pays appeal fees on behalf of x.

Honest user(s), who used their K votes to vote for x are faced with a dilemma. If they pay appeal fees on behalf of y, there will be an appeal which x is likely to win, so these appeal fees are lost. On the other hand, if the honest jurors do not appeal, x wins by default, but the final juror vote is for y and the honest jurors are considered incoherent and lose deposits of K*voteStake. Note again that the honest choice x is seen here as the winner by the arbitrable application regardless; hence this attack targets jurors rather than attempting to have malicious rulings adopted.

Then, we want to set parameters such that:

1) it will be in the interests of victims of this attack to appeal

2) if victims appeal, the attacker suffers losses compared to an expected return of feeForJuror*(M-K) that the attacker could obtain by honest participation.

How much it costs to trigger an appeal varies somewhat from application to application. Note that the dapps that use crowdfunding mechanisms as part of their Kleros appeal process have “stake multipliers” that determine the amounts that need to be raised on behalf of each side in order to trigger an appeal.

These values are currently such that the appeal costs to fund the winning side of the previous round are typically 1.5 - 2 times the cost of juror fees in the following appeal round and the appeal costs to fund the losing side of the previous round are typically 2-3 times the cost of the juror fees in the following appeal round. The amounts raised as part of the appeal costs beyond what is necessary to pay the juror fees in the triggered dispute are used as rewards for the crowdfunders of the other side if that side ultimately wins.

Then, the cost of paying the appeal fees for the next round, where there will be 2M+1 jurors is : feeForJuror*(2M+1)*(1+stakeMultiplier)

The juror can stand to gain (M-K)*voteStake+feeForJuror by having the last juror vote reverse its decision and rule for x versus if she does nothing then she will instead be penalized K*voteStake.

Then, the calculator attempts to find parameters so that :

Furthermore, if the juror pays the appeal fees, the attacker will receive some of her crowdfunding stake : (2M+1)*feeForJuror*stakeMultiplier. On the other hand, the attacker loses her vote stake for the votes she cast in the case : (M-K)*voteStake. So we want :

so that the attacker is incentivized to participate honestly rather than engage in this attack.

Note that this attack is mostly relevant in voting rounds where there are relatively few jurors, e.g. 3 or 7 jurors, because as a panel becomes larger it becomes less likely that the attacker can obtain a majority of the votes in the panel without actually possessing a majority of the stake. On the other hand, in voting rounds with only one juror such as the first round votes in the Humanity Court, this attack isn't relevant at all.

In v2, it is planned to integrate the crowdfunding mechanism into the Kleros court contract so that the court contract will have access to information about which alternatives were funded and can take that into account when rewarding or penalizing jurors. Then, the disconnect between what alternative is seen as the winner by the arbitrator and which alternative is seen as the winner by the arbitrable contract will no longer be present, and this attack will not be relevant.

Ultimately, we have developed a lot of confidence over the years in the crowdfunding mechanisms used by most Kleros arbitrable contracts, and giving arbitrable contracts the flexibility to deviate from this scheme in how they fund appeals does not seem to be worth the game theoretic issues that this disconnect can create.

Entering the estimates and using the calculator to find parameters that satisfy the constraints

If a user wants to update an existing court, she can enter her values for the various estimates we have discussed above into the section of the Colaboratory calculator that is labelled “Section for User to Complete to Update Existing Courts”.

The first values in this section are the estimates for crypto-prices and gas. Then, the estimates for the values of e, p, and t for each court are indicated in a list where the value in the jth place in the list corresponds to the estimate for the court with court id j. (Then the courts to which these values correspond are in the same order as the names of the courts in the box immediately above the “Section for User to Complete to Update Existing Courts”.)

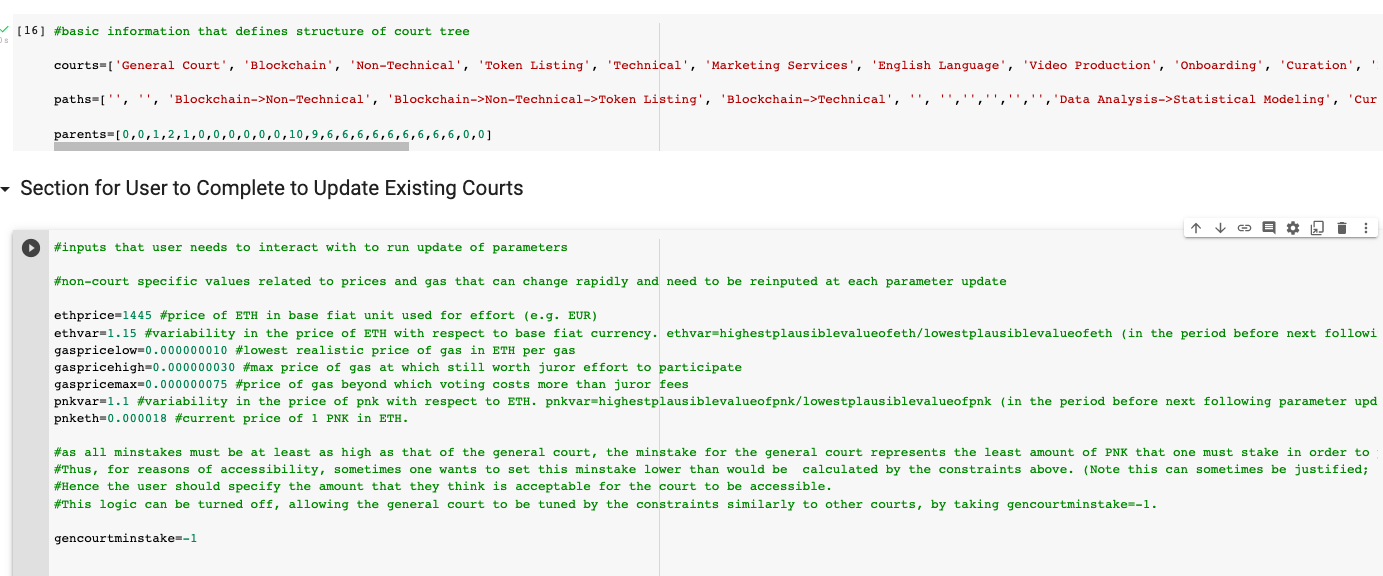
Then, also included in this section of the calculator are two toggles that are similarly given in lists ordered by court id:

1) “active” where by setting a toggle to 0 or 1 for each court, the user can tell the calculator whether to bother producing updated parameters for a given court. Some courts have been more active than others, and one can avoid updating the parameters of a court that is not currently being regularly used, at least to the degree that an update to some parameter in another court doesn't also require updating a parameter in an inactive court (for example, to satisfy the constraint that minStake should increase up each branch of the court tree).

2) “aaresistants” where by setting a toggle to 0 or 1 for each court, the user can tell the calculator whether or not to require resistant to the Arbitrator-Arbitrable split attack when updating the parameters for that court. In courts where the panels of jurors are not generally at a size where this attack is relevant, this toggle can be turned off.

Lists of the existing parameters are also included in oldfs, oldminstakes, and oldalphas, which give the current values of feeForJuror, minStake, and alpha, in each court respectively. This allows the calculator to determine the if the current parameters in a court are still appropriate.

Then, when one runs the calculator, it attempts to find values of feeForJuror and voteStake that satisfy all of the constraints that we have discussed above. Fortunately, if jurors are risk-neutral (more on this point below), then there will always exist a set of parameters that satisfy the constraints.

If a user wants to use the calculator to parameterize a new court, she performs a similar process entering the various estimations into the section of the calculator that is labelled “Section for User to Complete to Parameterize New Court”.

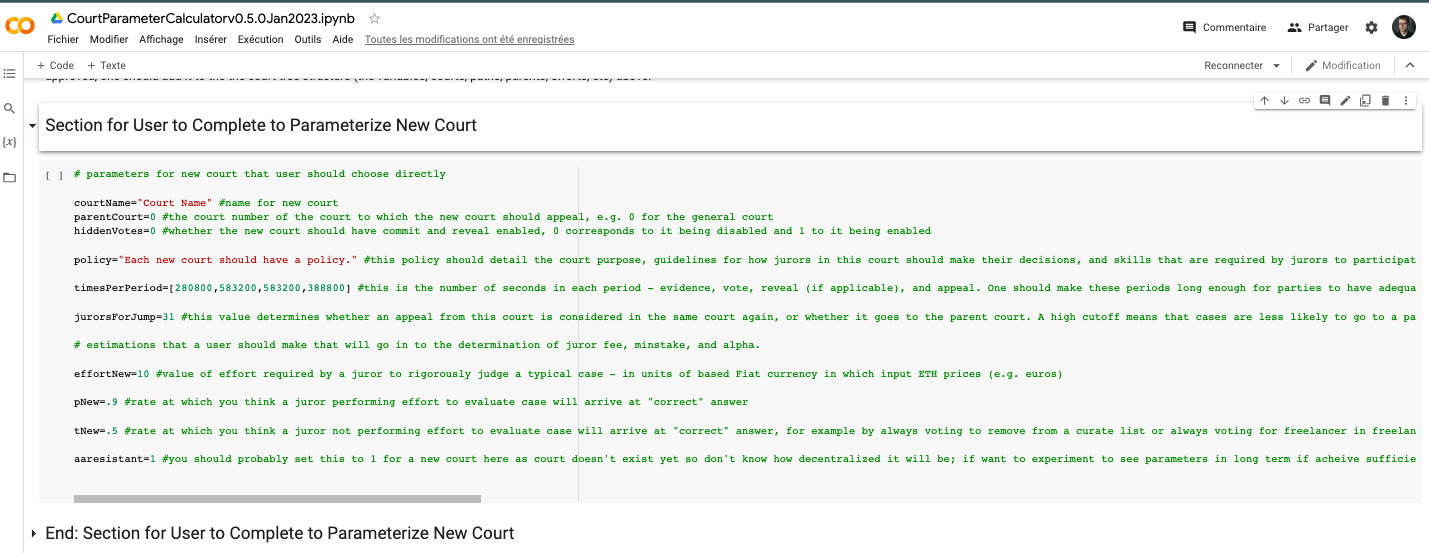
Here the calculator asks for the values of a parameters as well that the calculator does not calculate itself in order to remind the user to set values for these. While the calculations that we have been using to propose these parameters have not been as involved as those for feeForJuror, minStake, and alpha, there are still some useful heuristics that it is helpful to keep in mind when considering these values.

hiddenvotes

In the current version of the Kleros court contract, there is included functionality for a system of commit and reveal. Under this approach, in order for jurors to vote they must first make a transaction that "commits" to their vote. This means that the juror signs a transaction that includes a hash value where the inputs to the hash include the vote the juror makes, metadata about which case is being decided, and a random salt.

Then while an observer will be able to see that the juror has made this commitment, the observer will not know what alternative the juror voted for. Later, after all jurors have made their commitments during a "reveal phase" jurors need to make a second action where they reveal their vote and the random salt they used. Then the Kleros contract can check that this information corresponds to the juror's vote and use the revealed votes to tabulate the winning outcome.

For usability reasons, it was decided when writing the Kleros court contract to have this commit and reveal functionality depend on a parameter that is either activated or not. If jurors are required to make two actions to first commit and then come back to reveal their vote, they might forget to perform the reveal action. Both of these actions require issuing Ethereum transactions and hence paying gas. Also, as jurors need to have a reasonable amount of time perform both actions, the amount of time that each voting round takes is increased.

Indeed, in cases where one can expect incorrect rulings to be appealed we have reasoned that publicly visible votes (while not ideal) are not too problematic because a juror that observes how others are voting and thinks they are incorrect will still be incentivized to vote her true opinion if she expects that outcome to win an eventual appeal.

In fact because the redistribution of lost deposits in Kleros is done on a round by round basis, the lost deposits from jurors that are ruled incoherent will go to the other jurors in their voting round that voted for the outcome that ultimately wins the last round of juror voting. Thus, a juror that sees that other jurors are voting for an outcome that she expects to be overturned by an appeal, is that much more incentivized to vote for the outcome she believes represents the community's consensus.

Moreover, using commit and reveal still has its limitations in preventing vote copying behaviour. If an attacker thinks that by prematurely revealing her vote she can influence others nothing prevents her from doing so during the commit period. We have researched game theoretic mechanisms that can be used to discourage this type of behaviour in future versions. See the following talk for more information on this subject :

Nonetheless, if you expect your court to have cases that are less likely to be appealed, setting hiddenvotes to 1 and using commit and reveal is more important. Similarly making the UX sacrifices to use commit and reveal can be justified in courts that are handling weightier higher value cases. More generally, whether one uses commit and reveal can be thought of as weighing tradeoffs between usability and the healthy flow of information.

period lengths

The life cycle of a round of voting in a Kleros case is broken either into three or four periods depending on whether commit and reveal is activated or not. If commit and reveal is not used, then each voting round includes the following periods: 1) evidence period 2) voting period, and 3) appeal period. If commit and reveal is used, then each voting round includes: 1) evidence period, 2) commit period, 3) reveal period, 4) appeal period.

One should set periods that are long enough for the different participants to have ample time to perform their roles. Namely, the evidence period should be long enough for parties to argue their case, the vote period should be long enough for jurors to have time to review the evidence and vote, and the appeal period should allow for enough time for crowdfunders to consider the case and decide to fund an appeal or not.

Different period lengths will be appropriate for different types of cases. Jurors in smaller scale content moderation type cases do not need the same amount of time to read evidence and reflect as jurors in more involved cases. As most Kleros cases are not appealed, the total time of a single round of voting will be a typical resolution time, even if some contentious cases can take longer.

For now at least, there are likely minimum period lengths that are practical. Even the Kleros Curation court for example has an evidence period that lasts 1 day and 15 hours, a vote period that lasts 3 days and 9 hours, and an appeal period that lasts 2 days and 6 hours. Jurors with busy lives that are only ruling on a few Kleros disputes occasionally need time to notice that they have been drawn.

Moreover, on Ethereum mainnet gas prices are sufficiently volatile that one wouldn't want a period of less than at least a few hours as gas prices could be exceptionally high during the entire period, distorting the incentives of Kleros participants. Conceivably, if at some point there is a Kleros court in an environment that has consistently low gas prices (e.g. due to being on a rollup as if planned for v2) and where there is a sufficiently consistently high volume of small-scale micro-disputes that jurors can plan on staking for a few hours, solving the disputes in real time, and then unstaking when they are done, it could make sense to have significantly shorter period times.

jurorsForCourtJump

The jurorsForCourtJump parameter determines how many times a case can be appealed in a given court. Namely, if the number of jurors in the current round is less than jurorsForCourtJump, if there is another appeal the same court with consider the case just with a larger panel of jurors. On the other hand, if the number of jurors in the current round is greater than or equal to jurorsForCourtJump, then a subsequent appeal round will take place in the parent court of the current court.  

A notable special case concerns the role of the jurorsForCourtJump in the General Court. As a dispute cannot jump to a higher court than the General Court, if the  number of jurors in a given round in the General Court is greater than or equal to jurorsForCourtJump, then no further appeals are possible.

When a case is appealed to a parent court, a broader swath of the juror population considers it. In particular, the parent court will have a greater resistance to 51% attacks as it will be more difficult for an attacker to control the majority of stakes in that court. However, the jurors in the parent court will be less specialized in the type of dispute.

Thus, one wants to set jurorsForCourtJump lower in courts that one has some reason to believe to be more vulnerable to attacks so that one can more easily trigger an appeal to a more robust appeal court. This is particularly true for courts where less PNK is staked and which are consequently more vulnerable to 51% attacks.

Concretely, in a less robust court, the jurorsForCourtJump should be low enough that the community can reliably crowdfund the appeals required to send a case to a higher court.

Recall, as discussed above, dapps that use crowdfunding mechanisms as part of their Kleros appeal process have “stake multipliers” that determine the amounts that need to be raised on behalf of each side in order to trigger an appeal that are currently such that the appeal costs to fund the winning side of the previous round are typically 1.5 - 2 times the cost of juror fees in the following appeal round and the appeal costs to fund the losing side of the previous round are typically 2-3 times the cost of the juror fees in the following appeal round. The amounts raised as part of the appeal costs beyond what is necessary to pay the juror fees in the triggered dispute are used as rewards for the crowdfunders of the other side if that side ultimately wins.

Namely, in a court where resistance to 51% attacks is a concern, one should have confidence that the community is capable of crowdfunding the

that will be necessary to appeal a case that is being attacked from an initial round with three jurors to a round with seven jurors, then to a round with fifteen jours, etc all the way to a round with (roughly) jurorsForCourtJump jurors after which the case jumps to the parent court.

Absent such security concerns, one would generally want to set jurorsForCourtJump high enough to take advantage of the expertise of the specialized jurors who are staked in that court. Note, however, that beyond a certain point further appeals that draw upon the same pool of jurors become unlikely to obtain different results.

For example, imagine that a proportion of π of tokens staked in the general court correspond to people who would vote x on a case and 1-π correspond to people who would vote y on a case. Then if π>.5, x represents the outcome you would get if you had a sufficiently large sample of jurors. However, there is always some possibility that the panel of jurors that is randomly selected in a given round will not be representative of the broader community and would vote for y.

Using a calculator that estimates the tails of binomial probability distributions, one can find the probabilities of getting a majority of votes for y for different values of π and for different panel sizes :

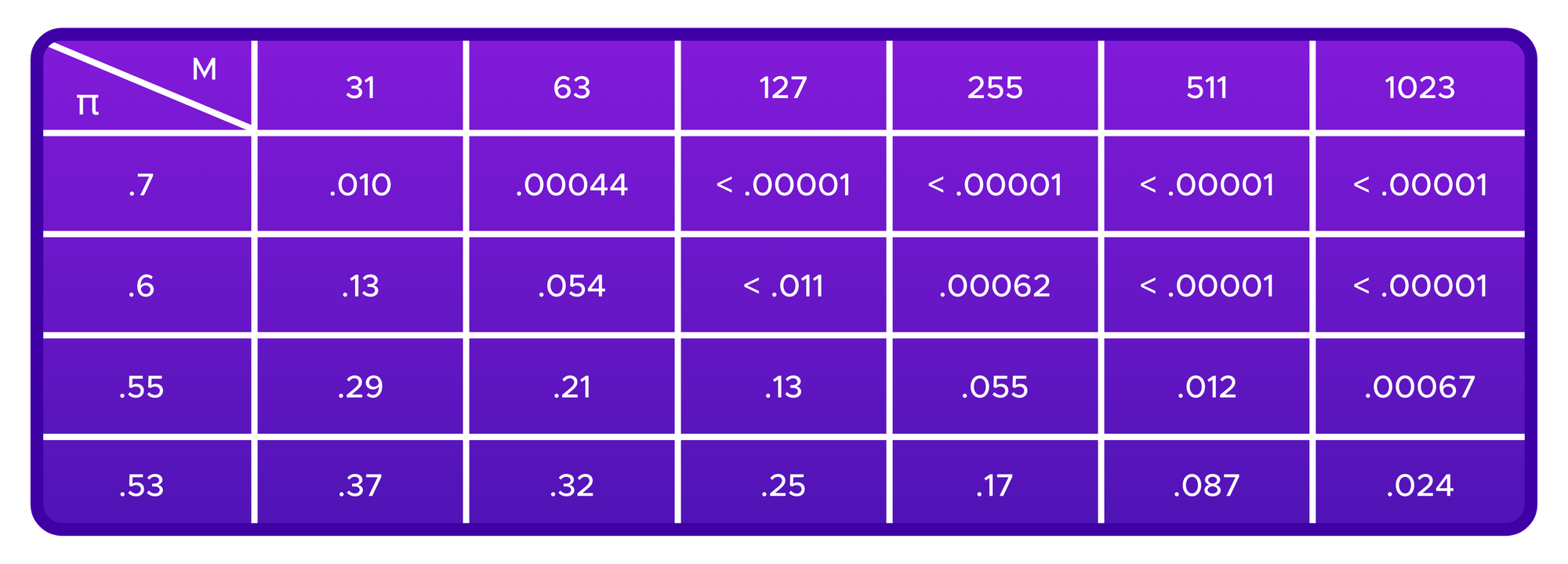
This gives a sense of how close an “edge case” needs to be for an extra round of voting to be likely to make a difference. We see that even if a court has a fairly low value of jurorsForCourtJump, it is very likely to produce a panel that represents the community consensus on more clearcut "70-30" type cases and a subsequent round in that court is unlikely to produce different results. However, for less clearcut “55-45” or “53-47” type case an extra round in a court can be meaningful in getting a clear sense of the consensus opinion of jurors in that court.

When setting the jurorsForCourtJump parameter for the General Court there aren't the same considerations around tradeoffs between specialization and 51% attack resistance. Nevertheless, one can perform calculations similar to those above to consider the point at which sampling error is sufficiently low that a future round in the General Court has a high probability of producing a similar result to the previous rounds.

However, there are other considerations around setting the jurorsForCourtJump in the General Court that are unique to this court, as this sets the limit at which cases become unappealable. The possibility for further appeals contributes to a lot of game theoretic defenses in Kleros against various attacks including bribes, p+epsilon attacks, and pre-revelation attacks. Some but not all of these game theoretic advantages are reduced when you get to the point of drawing such a large sample of jurors compared to the amounts people have staked that a subsequent draw is statistically very likely to just give you back the same people.

For p+epsilon attacks, in particular there are important "last round effects" that impact attack resistance. Two basic strategies for this attack that we have explored in our research are the following :

1) The attacker can offer the p+epsilon bribe to jurors judging the case in the current voting round and credibly commit to continue the attack in future voting rounds to discourage crowdfunders from appealing the case so that the corrupted result of the current round is not overturned. In order to be able to credibly commit to being able to continue the bribe through all possible appeal rounds, we have noted that the attacker needs to lock up a budget in PNK that is at least

For example, with the current General Court parameters where voteStake=1700 PNK and jurorsForCourtJump=511, a second to last round of a case that was appealed the maximum number of times would typically have 255 many jurors, so an attacker would need a budget of around 110 million PNK to attempt this attack.

2) The attacker doesn't offer bribes in early voting rounds. However, she appeals every voting round herself, regardless of its result, until one arrives at the last possible appeal round. Then, in this last possible round, she offers a p+epsilon bribe. This would typically require a budget for the attacker that is a linear multiple of the total arbitration fees in the case.

Note that the second possibility could be eliminated entirely if one sets jurorsForCourtJump in the general court to an unattainably large value. Moreover, if one makes this choice, the number of jurors in the "second to last possible round" would also be unbounded, so the amount that the attacker needs to lock up in PNK to credibly commit to being able to maintain the attack through its possible appeals would be larger than the PNK supply. Other variants on the p+epsilon attack would still be possible, though they would be more complicated for an attacker to communicate to jurors and correspondingly have to contend with higher cognitive costs.

However, such an approach means that the maximum dispute resolution time would also be unbounded. Having an upper bound on total resolution time can be important for some applications; also it puts a cap on the total amount of time that a well-funded actor can delay a decision. In general, each additional round of appeal that is possible in the General Court increases the maximum possible time that a dispute can take to be resolved. Currently, each additional round in the General Court, using the current parameters for period lengths, adds an 14.5 days to the total length of the dispute.

In any event, it can be useful to err on the side of having the possibility for a few appeal rounds beyond what is typically reached so that one only has unappealable rounds in very rare occasions. Note that in v2, if there are enough appeals, the plan is just to go to a module where there is no more random sampling and instead everyone votes. As part of this process, participants will also express a preference on whether they think the court should fork if their side loses. Particularly, attempting a p+epsilon attack against this "fork vote" should have costs comparable to those of a 51% attack.

A few more subtle points

Risk-aversion

In much of the analysis above, we have sought to make sure that average returns of honest participants is positive while average returns of dishonest participants is negative. However, note that focusing on the average return can gloss over other important information in the distributions of returns of participants.

Particularly, human beings are often risk-averse, so a distribution of returns where they have a small chance of a very negative return may not be attractive even if the expected value of their return is positive. This is particularly true if a juror is only drawn on a relatively small number of cases, so they can't necessarily count on the variation in their returns averaging out.

There are various ways of modeling risk-aversion. A relatively simple approach is to estimate a coefficient of risk-aversion λ and then any positive returns for the user are weighted normally, while negative returns are weighted by λ. Taking this approach the constraint that honest participants that make an effort of e to review cases will receive an expected return, weighted for risk-aversion of :

Then, as above, we would want to choose parameters to make this formula positive in order to make sure it is worthwhile for jurors to participate honestly in the protocol.

Indeed, the Colaboraty calculator has an input for the risk-aversion of the population of users. Similar to juror effort in evaluating cases, this is a value that is difficult to estimate based on on-chain information and is best estimated by the users who participate as jurors in Kleros. Note that the current version of the Colaboraty calculator does not apply the risk-aversion coefficients to attackers as one is mostly worried about attackers that would repeat a malicious strategy a sufficient number of times for their risk to average out.

We noted above that a set of parameters that satisfy the constraints we considered above always existed if the users were risk-neutral. This is due to the observation that, for sufficiently large voteStake, there will be some feeForJuror that satisfies all of the constraints. However, we are no longer guaranteed to have a set of compatible parameters if the population of jurors is sufficiently risk-averse as increases in voteStake are weighted more heavily in their considerations.

Parameters that can updated or not

Finally, note that while most of the parameters that we have considered in this article can be updated by subsequent votes of Kleros governance, there are a few parameters for which this is not the case. Specifically, there are functions in the Kleros smart contract to update feeForJuror, minStake, alpha, jurorsForCourtJump, and the various period times.  

While there is not a smart contract function to directly update a court policy, the policy in a given court is essentially a matter of social consensus and the community can vote to change what it views the policy to be. Hence, if you propose a new court and you realize that some of the parameters were not optimally set the community can iterate on its experiences and eventually adopt more appropriate parameters.

On the other hand, a few parameters cannot be updated on courts that have already been deployed. In v1 of Kleros this includes parentCourt and hiddenvotes; in v2 of Kleros hiddenvotes is planned to also be updatable. The parameters that cannot be updated of course deserve particular attention when proposing a new court.

Conclusion

We have detailed the ways we have thought about setting court parameters in v1 of Kleros.  A user parameterizing a new court or updating the parameters for an existing court can focus on obtaining good estimates of the effort required to analyze the cases in this court and the level of subjectivity of the cases. Then one can use these estimates as inputs to the Colaboraty calculator we have developed  which will return many of the parameters that are necessary. We have also discussed a few heuristics for how to think about the remaining parameters that the calculator does not produce.

Of course, in the future one may improve upon the calculator that we are using. We have discussed how the various constraints and heuristics that we employ are designed around making Kleros resistant to a wide variety of attacks and undesirable behaviour, including: lazy voting attacks, arbitrator-arbitrable split attacks, frivolous appeal attacks, 51% attacks, and p+epsilon attacks. Further research may improve our understanding of resistance to these attacks or identify new vectors of attacks which can be taken into account in future versions of the parameter calculator.

Also, as the modular design of the upcoming v2 of Kleros will allow different courts to use different voting and incentive systems, parameterizing different courts in v2 may require different considerations. In situations where one has largely binary disputes and can use a voting and incentive system similar to that in v1 of Kleros, most of the ideas we have discussed will continue to apply. In Section 4.7.5 of the Kleros Yellowpaper we have already modeled some parameter considerations in voting and incentive systems designed to better handle non-binary cases. Future research may find that other voting systems are also appropriate for certain types of cases, and then one would need to consider how to appropriately parameterize those systems.

Another improvement that could be possible in future versions of Kleros could include having parameters that, at least partially self-adjust. Much of the information that we have discussed using above to update parameters is available, in some form, on-chain. However, allowing a smart contract to access this information in a way that is attack-resistant is often a challenging problem. Nonetheless, in the long-term if these challenges are resolved, one could image agile parameters that adapt in real-time to changing conditions, similar to the mechanics around Uber surge pricing.  Then governance votes would only be necessary if one wants to change the formulas that the parameters are updating according to.