Doges on Trial第3部分 - 加密经济模型原理 最终版
在本系列的前两篇文章中,我们看到了陪审团投票模式的一些广泛趋势,然后我们仔细研究了攻击者试图贿赂陪审员的案例。 在本文中,我们将探讨其他一些有趣的问题和观察结果,这些问题和观察结果是关于陪审团在Doges on Trial试验中的一些行为。
By William George
在本系列的前两篇文章中,我们看到了陪审团投票模式的一些广泛趋势,然后我们仔细研究了攻击者试图贿赂陪审员的案例。 在本文中,我们将探讨其他一些有趣的问题和观察结果,这些问题和观察结果是关于陪审团在Doges on Trial试验中的一些行为。
“懒惰策略”:总是投票给最常见的反应
在我们系列的第一篇文章中,我们看到大约70%的票都投给了“ not doge”。然后,人们可能自然而然地会问,如果我建立一个存放PNK的机器人,不管图片长什么样我都只投“ not doge”票,这样是否有利可图?
作一个粗略式的启发,假设我们在每种情况下都给这样一个攻击者一票,但为了简单起见,所有现有的投票仍然有效,并假设案例的最终结果不会受影响(毕竟,如果这个攻击者导致了不公正的结果,可能会被上诉)。 然后,如果我们分别用Ni和Di表示第i个案例中的“not doge”和“doge”票数,如果d是陪审员投出的不一致的票,则攻击者的净收益由下式给出:

根据观察到的每种情况下的Di和Ni值(截止到disputeID为148,有资格获得Dogecoins的奖励),我们计算出S = -48.9d,也就是说,使用这样的懒人策略,扣除PNK盈利,攻击者(矿工)仍将损失48.9个存款(如果所有票都投 “doge”,则损失更为惨重,等效计算得出S = -78.3d)。
很显然这个策略行不通,如果攻击者(矿工)不假思索的投票的话,他将一无所获。我们也已经看到,大多数案例实际上是一致的。
对这个问题的更完整答案将取决于攻击者控制的PNK总量的百分比,进而我们可以推出攻击者在第i个案例中被吸引的可能性并计算她的预期回报。 或者,我们也可以换个角度思考,考虑到攻击者在上诉时可能会有更多的选票,当有更多的总票数时,以及那些案例是最有可能使攻击者受益的,因为他们往往是有争议的。由此,我们可以根据计算的总票数对案例进行权衡:

注意,通过不调整Ni + 1分母来反映攻击者拥有更多的选票,我们实际上高估了攻击者的收益,而忽略了由于攻击者不连贯时造成的损失的影响。 在这里,计算结果S'= - 101.3d(如果所有票都投 “doge”,则S'= - 645.1d),所以,基于以上的假设,这种懒人策略仍旧是行不通的。
证据和威尼斯Doges
Doge实际上是Shiba Inu一个心爱的模因形象。 然而,早在这个模因创作之前,Doge这个词就被用来指代威尼斯共和国的首席法官。 当我们问陪审员“这张图片是否显示一个Doge?”时,他们可能会合理地把威尼斯的法官莱昂纳多·洛雷安的肖像归类为Doge:

然而,也有可能是这种情况,一位了解威尼斯历史的陪审员,她可能认为其他的陪审员并不了解威尼斯的历史,不知道威尼斯曾经被Doges统治过,即使她认为诚实的回答应该是“doge”,而为了保持裁决的一致性,她也可能投了“not doge”票。
这种现象是陪审员面对有争议的案例时,作出裁决的重要基础,此时他们有足够的信息来作出明智的判断。 一般而言,我们期望各证据方所提供的证据,会对陪审员的裁决产生重要影响。 对于Doge试验,我们没有向提交者或挑战者提供明确的机制,该如何向陪审员提供证据。但是,提交者可以在其图像中嵌入文本,例如在序列提交中:

另一方面,以下类似的提交收到了一些更复杂的结果,尽管已经为陪审员提供了足够的指示,以便他们能够做出明智的选择:

或许,Paolo Lucio Anafesto的结果比Leonardo Loredan更糟糕的原因可能与历史上是否真正存在Doge Anafesto的这一历史性谜题有关,这一争议在陪审员面前被使用了短语“相信是”来表达。事实上,证明Anafesto存在的第一个历史记录可以追溯到11世纪。
尽管如此,为陪审员提供相关证据似乎可以提高他们共同转向明智选择的能力。 我们期望在未来进一步调查证据的影响和作用。
同时包含狗和猫的图像
图像中同时包含doges和猫的情况引起了极大的争议。针对将猫图像放到列表上的奖励政策,Kleros明确指出同时包含一个doge的图像不符合奖励条件。
但是,子廷政策只关心图像中是否包含一个doge。
随着时间的推移,似乎有将这些图像全部归为“ not doge”的趋势。实际上,我们选出了11张同时包含Shiba Inu和猫的图像。 所有这11张图都受到了挑战:在八月初共有72名陪审员参与的投票中,其中两张图被判定为doge,其他九张均被拒绝。


执行逻辑回归,来预测陪审员对某张图投 “doge”票的概率,将该图像最后一次活动的日期(提交,挑战,上诉等)用函数表示,我们得到这样一个模型:
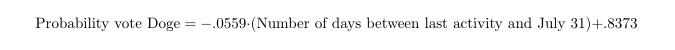
对应斜率是否为负的p值为.0013,该统计证据表明,随着时间的推移,陪审员越来越不愿意对这些图像投 “doge”票。

事实上,大多数最近的案例都被一致投票为“ not doge”。因此,当陪审员面临可能被解释为含糊不清的情况时,在经历了一些早期有争议的案例之后,就自然而然形成了一种先例。 然后,提交者,挑战者和陪审员都可以合理地预测这些图像将如何被裁决 。
分析陪审员是否看过区块链上的已存在的投票结果
在当前Doge试验中,评审员一旦投票,区块链中就可以看到该投票结果。 (从长远来看,我们打算采用某种提交和显示机制,以便使投票结果在整个投票期间处于保密状态。)这意味着对每个案例进行投票的最后几个人可以先查看链上投票结果再进行投票,以确保最终投票结果的一致性。
值得注意的是,对陪审员投票结果是否一致的奖励和惩罚,与该案例的最终结果有关。 因此,如果你认为陪审员的裁决会被上诉的话,或许你应该反其道而行之,投出与大多数评审员不一致的票。
实际上,如果你认为错误的裁决最终会被上诉,那么你应该思考的是,在未来的上诉中,绝大部分未知的“理想陪审员”会如何投票,进而作出你认为正确的选择,而无需在意当前的投票总数。
尽管如此,如果有少数的不连贯的投票,且他们的投票时间都很迟,而这些不连贯的投票导致了本轮投票产生不同的结果,我们就可以认为,陪审员实际上正在查看链上的其他投票结果。
排除正在进行p + epsilon攻击的情况,截止到RapportID 148,在第一轮投票中有16个非一致决定(2-1),在第二轮中有10个非一致决定(4-3, 5-2或6-1)。 在这26轮投票中,总共有35张票投在失败方。 在这35张票中,有11票是在获胜方占多数后投票的。
如果我们相信这一假设——陪审员没有看过区块链中先前投票结果,那么我们可能会认为特定情况下“doge”和“not doge”投票的顺序是随机的。 也就是说,当出现doge 2-1的结果时,以下三种投票顺序都有可能出现:
doge - doge - not doge
doge - not doge - doge 和
not doge - doge - doge
也就是说,有三分之一的时间我们应该看到“doge - doge - not doge”的情况,就是最后一名陪审员在该轮的结果已经确定之后投了不一致的票。如果两票“doge”归属于同一位陪审员,那么“doge - not doge - doge”的情况就不可能出现,因为投票结果是按照评审员地址归类的。 所以在这种情况下,如果投票的顺序是随机的,我们可能会看到以下两种情况以相同频率出现:
doge - doge - not doge 和
not doge - doge - doge
当裁决结果被上诉时也是如此,例如我们有一个2-5“not doge”的决定,其中有五个不同的陪审员地址投票:
A (2 votes) doge
B (2 votes) not doge
C (1 vote) not doge
D (1 vote) not doge
E (1 vote) not doge
总共有5个选项! A,B,C,D和E的投票结果可以有多种排序方式。 其中,为了在已经有4个“not doge”投票之后投“doge”票,前三位投票中B必须出现, C,D,E必须出现两个,出现顺序不一定。还有很多

这样的排序。因此,如果A,B,C,D和E的顺序是随机的,
出现两个不连贯的投票的概率为.3,

而一个不连贯的投票都没有的概率为.7。
(注意事项:当然,我们可能有一些逆向陪审员,他们也恰好在每个投票期开始时参与。因此,不同的投票将集中在每个案例的第一轮投票中,即便陪审员没有看区块链上的投票,考虑到投票的图像的多样性和每个投票期开始时间的变化,我们假设这些影响可以忽略不计。我们也会假设不同案例中投票的顺序是独立的。在实践中,陪审员通常会同时对所有案例进行投票。因此,如果同一个人尝试不连贯投票,他们在同一轮投票中的不连贯性可能在不同投票顺序中差别不大。但是,由于这些非一致的案例分布在许多投票期,而且出现不一致投票的陪审员往往也不一样,其产生的影响都可以忽略不计。)
对于我们所拥有的每一个非一致结果,推理是这样的,考虑到每种情况下由每个地址控制的投票数,并假设每个案例的投票顺序是独立的,则多数投票结果确定后,出现不连贯的投票数的分布如下:
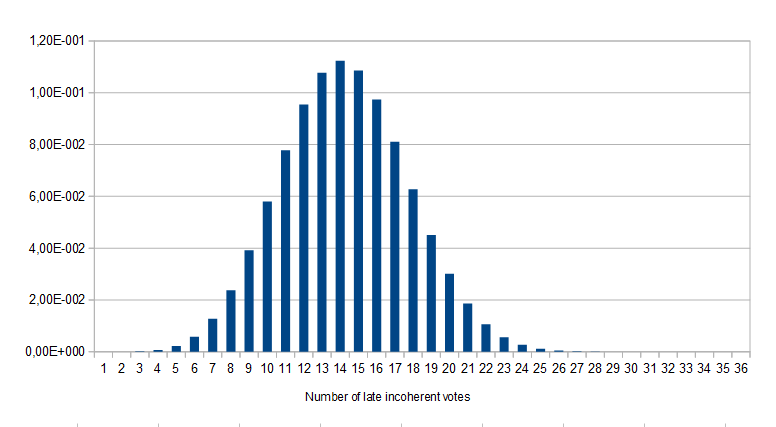
我们再次观察了11轮此类投票。 该分布的预期值为13.250,即所观察到的后期非一致性投票的数量略少于预期,而我们观察的p值为.315716。 因此,至少到目前为止,我们没有令人信服的统计证据表明陪审员在裁决前查询了区块链上的投票结果。 (当然,如果有足够的额外数据,我们可能会找到这种行为的证据。这个试验至少为我们提供了一个方法,当有足够多的陪审员在投票之前查看以前的投票结果时,是否以及何时才能在统计上注意到这一点。)
结论
在本系列的前两篇文章中,我们已经看到Doges on Trial试验对51%的攻击和p + epsilon攻击表现出相当大的抵抗能力。 在本文中,我们进一步观察到对懒惰投票攻击的抵抗能力,我们关于连贯和不连贯投票顺序的讨论让我们了解试验对预启示攻击的敏感性。
此外,我们已经开始观察证据的影响和先例发展的影响。这种现象对于争议解决系统的稳定性和可预测性至关重要,我们期望对这些影响进一步研究。

加入 Kleros!
加入电报社群 Telegram.
网站 website.
推特 Twitter.
开发人员 Slack .
开源贡献 Github.




