Kleros and UMA

Smart contracts are powerful organizational tools that have the potential to allow novel types of economic arrangements. However, as they cannot natively observe information that is not part of their blockchain’s consensus algorithm, they need access to oracles that can provide them with real-world information that they might require. Often this information is subjective and requires the input of human beings. An insurance contract against smart contract hacks needs to know whether there has been a hack. Similarly, a contract used by decentralized social network needs to know whether submitted content is allowed under the community’s policies.

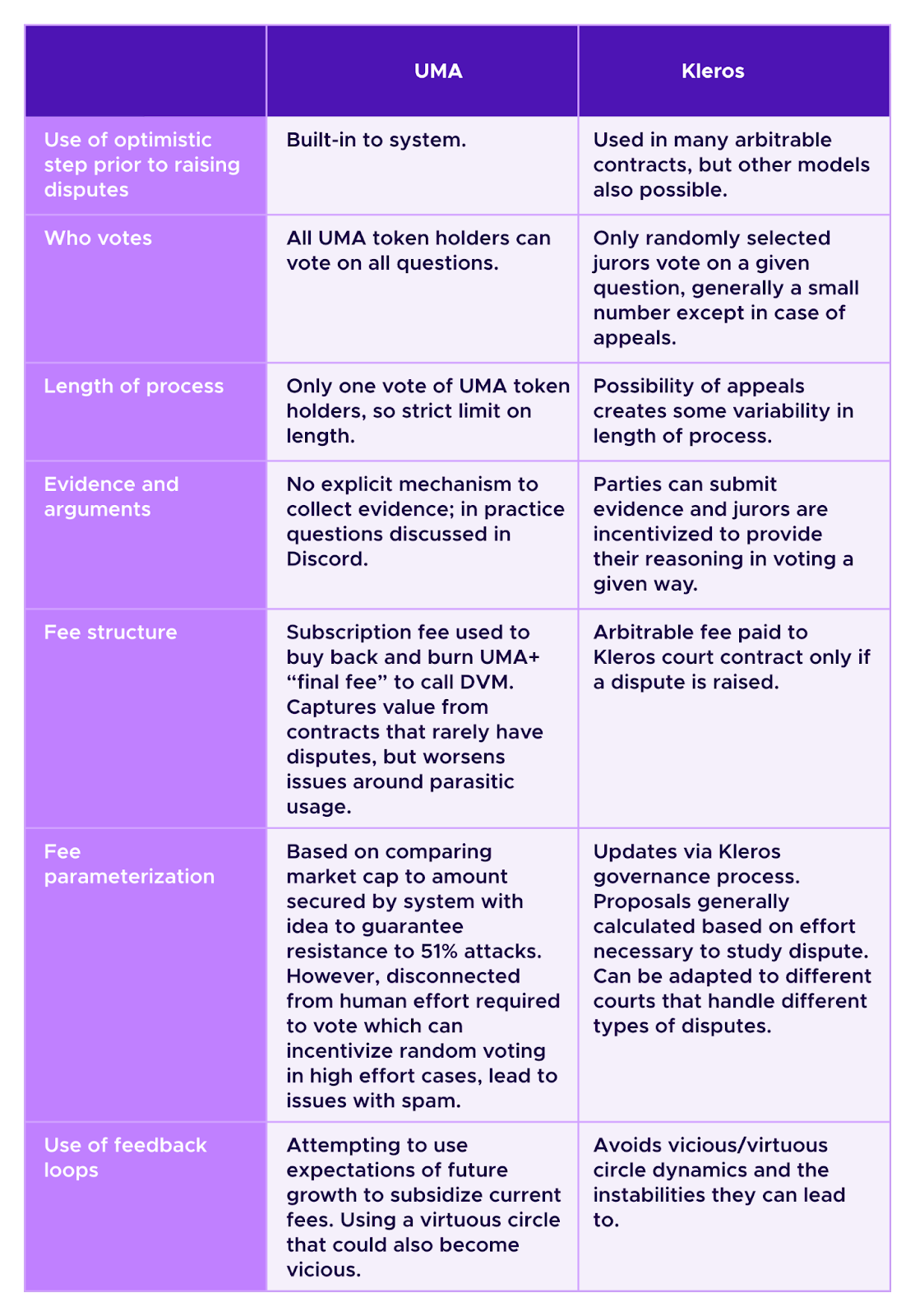
Kleros and UMA are both oracles that use Schelling-point mechanisms to coordinate human responses to questions. Namely, participants in both systems vote on questions presented to the respective oracles and receive rewards if they agree with the collective response of the system. As such, the participants are playing a coordination game where one thinks of “true” outcomes as being focal points.

While they have many similarities, the two projects have made different design choices on some important points. In this article, we will describe these similarities and differences.

Use of “optimistic” steps

UMA considers itself an “optimistic oracle”. Namely, as a first step in all questions in UMA, “proposers” can place a bond and provide a response. Then “disputers” can object to this information by also placing a bond. This escalates the question to a vote of UMA token holders. If no one disputes the information within a given challenge period, the oracle accepts that information as being correct. This process is similar in spirit to the “optimistic” logic underlying optimistic rollups, where individuals can submit commitments to updates on the state of the rollup to L1 which can similarly be challenged by a fraud proof created by someone who notices that this state update is incorrect.

In Kleros, we have a notion of “arbitrator” and “arbitrable” contracts, each with certain basic requirements under ERC-792. This standard is designed to be very flexible in that arbitrable contracts can be written with different types of logic about when disputes should be sent to the arbitrator. Then it is the Kleros arbitrator contract that encodes the Schelling-point based game in which random jurors are chosen and incentivized to study and vote on disputes.

Often arbitrable contracts using Kleros also use optimistic logic. For example, in curated lists such as Tokens and Proof of Humanity, one can submit entries to the lists along with a deposit. Then a dispute is only raised on Kleros if this submission is challenged by another actor placing a deposit. Indeed, by asking an arbitrary question to Reality.eth and choosing Kleros as the arbitrator, one can achieve a similar experience to that of UMA. Reality.eth allows for multiple rounds of users placing bonds on an answer to a question in contrast to the single round mechanism of the optimistic step in UMA. However, as Reality.eth bonds must at least double in each round, this process can be quite fast. Also, if a party wants to accelerate the process and is sure of the information she is providing, she can place bonds that are more than double the previous bond.

However, if one has an application where one requires particularly robust information and has higher tolerance to fees, one can also write an arbitrable contract that systematically calls the arbitrator everytime it needs information.

Hence, one can think of the Kleros arbitrator contract as equivalent to UMA Data Verification Mechanism (DVM). The optimistic step in UMA is equivalent to one type of oracle approach that arbitrable contract can use, though in Kleros other models are also possible.

One round resolution versus an appeal system

A fundamental difference is that in Kleros there is a notion of an “appeal”, where after a group of randomly-chosen jurors vote on a decision the contract can be triggered to draw a larger panel of randomly-chosen jurors who reconsider the case. In Kleros, jurors are incentivized to agree with the decision of the last round of juror voting (which may not be the same decision as that taken by a juror's own round of voting). In contrast, in UMA, once a question goes to the DVM, there is only a single round of voting, in which all UMA holders can participate.

This choice has important consequences for the two platforms :

1. Speed of resolution process
   • In Kleros, as each appeal round results in the new jurors being given time to consider the case, there is some variability in how long a case will take to resolve depending on how many times it is appealed. Indeed, sometimes attackers can trigger appeals intentionally to delay the resolution of a case. However, as the required appeal fees grow exponentially from one round to the next, the attacker will only be able to continue this process for a limited number of rounds.
   • As there is only one round of voting in the UMA DVM, all cases take roughly the same amount of time to resolve. This provides strong guarantees on when a decision is available. Currently, a UMA vote lasts for approximately two days.
2. Duplication of voter effort
   • In Kleros, only a few randomly selected jurors will have to spend the human effort to evaluate a case in a given round. Nonetheless, as jurors know that their rewards and penalties depend on whether they agree with the outcome of any possible future appeals, they are incentivized to try to vote in a way that is representative of the broader pool of staked PNK holders. Then, one only needs to require many jurors to spend the effort required to evaluate a given case if the case is appealed enough times.
   • In the UMA DVM, all token holders can vote on any question. Indeed, in order for the platform to be secure a large percentage of all token holders must vote in each question so that an attacker cannot sneak through a malicious outcome in a low-turnout vote. Thus, a large percentage of all token holders have to spent to effort to review each question, resulting in a significant duplication of effort. This effect is particularly relevant for complex cases that require more effort.

In the past, we wrote a similar analysis comparing Kleros and Augur. There, the structure of the appeal systems, and the level of complexity of questions the systems were correspondingly calibrated for, was also an important point of comparison. Specifically, we saw that Augur used a de facto appeal system where the current outcome of a question can be disputed by staking enough REP on another outcome. This leads to questions remaining open as larger amounts of REP are staked on opposing sides, preventing an attacker from winning a low turnout vote on a question as long as honest parties can stake enough REP on the opposing side to move to a subsequent dispute round. As this process continues, questions that initially do not receive much attention can eventually represent large enough stakes that they are noticed and evaluated by the broader community. Hence, this mechanism can lead to more duplication of effort than that of Kleros, where the effort is concentrated on specifically chosen jurors. However, it requires less duplication of effort than a call to the UMA DVM.

Hence, one can potentially think of questions that might be posed to these oracle systems as living on a spectrum by their level of complexity, where UMA is appropriate for the least complex cases, Kleros can handle the most complex cases and Augur is in the middle.

Arguments and evidence

In Kleros there is a period where parties to a dispute can submit evidence in support of their case. Moreover, jurors are encouraged to provide arguments for why the ruled a given way. These arguments are visible to jurors in future appeal rounds, so if a juror provides solid arguments she increases the chance that the ultimate appeal round will side with her point of view which determines whether she is rewarded or penalized.

In contrast, UMA has no explicit process for gathering evidence and arguments, though in practice voters tend to discuss cases in the UMA Discord. (Similarly, Kleros jurors often discuss ongoing cases on Telegram.) While, this can be appropriate for straightforward decisions, at Kleros we feel that the having a process to organize arguments and collect jurors’ rationales is important for a dispute resolution process to be able to make subtile decisions that will be accepted as fair by parties.

Fee philosophy

In UMA, voters in the DVM that vote with the winning outcome are rewarded in newly minted UMA tokens.

Then, UMA imposes two types of fees on users and applications that ask questions:

• A subscription-type fee is used to buy back and burn UMA tokens. Contracts must register with the UMA in order to access oracle services. Then, registered contracts pay this fee, even if all of their questions are being resolved by the optimistic, Submitter-Challenger step, in order to remain eligible for resolution by the UMA DVM should it be necessary.
• Additionally, an anti-spam fee called the “final fee” is paid to call the UMA DVM. This fee is currently .35 WETH, 1500 DAI, or 250 UMA depending on the collateral currency being used by the relevant contract.

The UMA subscription fees are determined in terms of how much value the system is securing compared to estimates of how much it would cost to attack the system by buying half of the UMA tokens and taking control of the DVM. Namely, contracts using UMA must be formatted in such a way that UMA is aware of the total amounts at stake. In the UMA whitepaper these amounts are called “profit from corruption” as they represent the amounts that an attacker could conceivably exploit if she gained control of the network by obtaining over 50% of UMA tokens.

Then, if F is the total subscription fee paid per unit time, individual contracts that are registered with UMA are required to pay a proportion of F that corresponds to their individual contributions to the total “profit from corruption”. Namely each contract must pay:

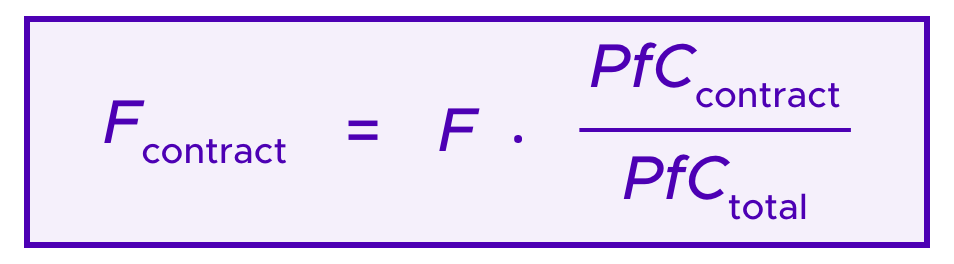
The total subscription fees F are adjusted based on whether the UMA contract thinks that adequate security is being provided for the amounts at stake. Namely, it compares the total “profit from corruption” to the cost of buying enough tokens to present a threat of taking over the system, called the “cost of corruption” in the UMA whitepaper. If the “cost of corruption” is considered to be excessively high enough compared to the “profit from corruption”, F decreases. If the “profit from corruption” is too high compared to the “cost of corruption”, F increases and the fees collected are used to buy back and burn UMA tokens with the idea of increasing the price and hence the “cost of corruption”.

Currently, F is zero in UMA. Namely, applications using UMA as an oracle are not paying any subscription fees. The UMA whitepaper attributes this to “expectations on growth” sustaining the price of UMA tokens beyond what is necessary to secure current usage of the system. The UMA whitepaper continues by writing “This is no free lunch; fees will ultimately be levied at a future steady state when there is no expected growth in the usage of the system”.

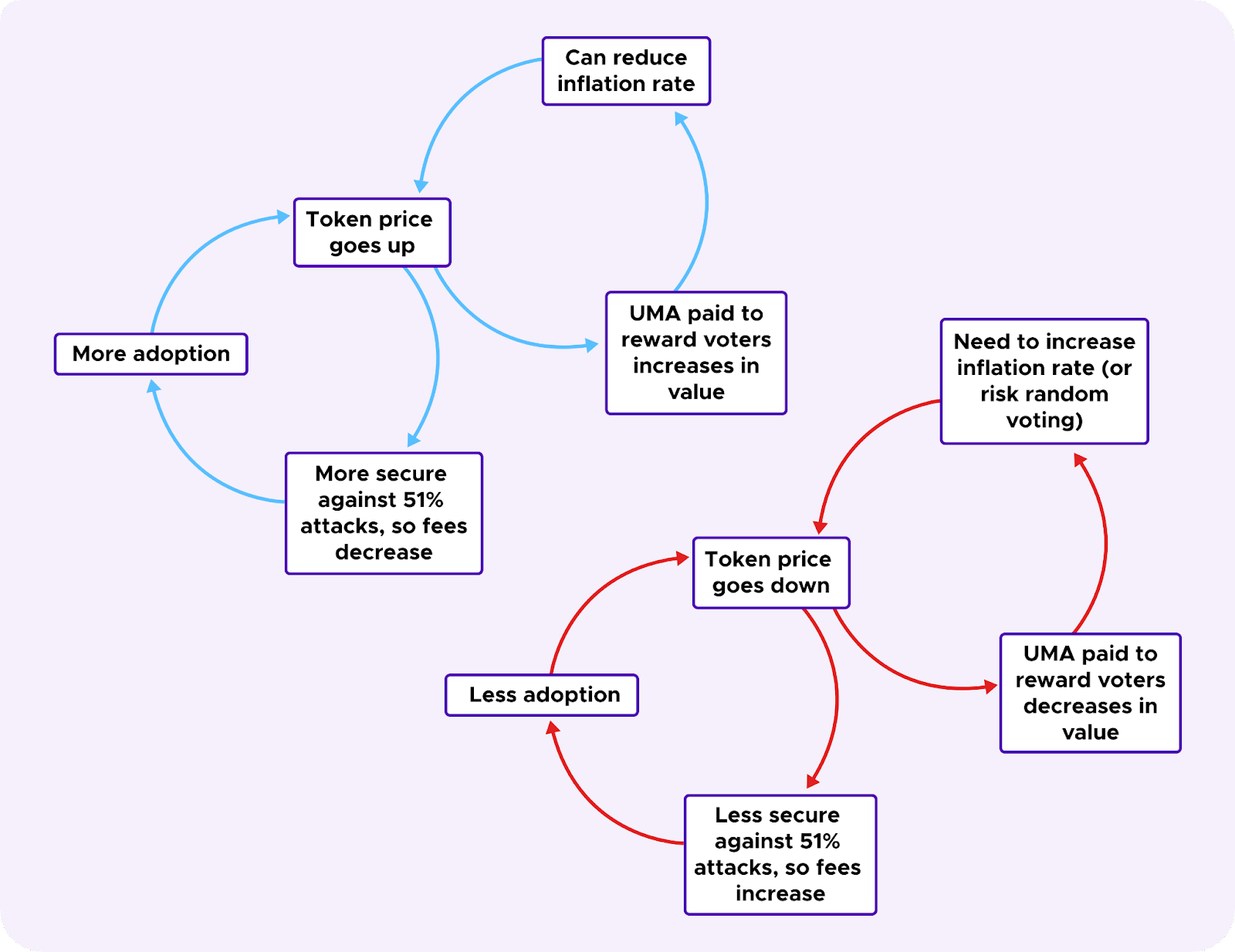
Essentially, UMA is currently benefiting from a virtuous circle : applications seeking oracle information can benefit from low fees, which can attract new users and lead to further expectations of growth. This can positively effect the token price so that the contracts still see the “cost of corruption” as being high enough compared to the increased “profit from corruption” that fees can remain low. Moreover, in such a dynamic, UMA token holders may be willing to accept that new tokens are being minted with each question as rewards in excess of what is being burned from fees.

However, this circle can also run backwards and become vicious. If the token price falls and the “cost of corruption” becomes too low compared to the “profit from corruption”, the protocol will attempt to adjust by raising fees. This can create friction for the users of contracts requiring oracle services leading some to consider other oracles and rendering some use cases unviable. This can potentially damage expectations of future growth and cause the token to fall further.

Moreover, as UMA voters are rewarded in terms of UMA tokens, if the value of the token decreases it becomes less attractive to spend time and effort to vote on a question. If a lower percentage of participants vote (leading to reduced attack resistance) or participants are inclined to vote randomly, this can further undermine perceptions of the system. However, if the amount of UMA tokens minted per question is increased to attempt to maintain comparable incentives for voters either F will need to increase even more, beyond the buyback amount targeted to restore the guarantees on cost of corruption versus profit from corruption, or there will be inflation leading to further negative impacts on token price.

On the other hand, in Kleros, fees in ETH (or in Gnosis chain version of Kleros in xDAI) are paid to jurors that vote for the outcome that ultimately wins the final vote. Note that users of arbitrable contracts only have to interact with the native token of the chain. While jurors can lose staked PNK if they vote for non-winning options, this PNK is redistributed to the jurors that voted for the outcome that wins the final vote. Hence, PNK is neither burned nor created in this process.

The fees paid to Kleros jurors are generally calculated in terms of the effort that is required for jurors to analyze a given case. Kleros has a system based on a court tree, where different courts are specialized in different types of cases. All courts are appealable to the Kleros General Court, where all jurors are staked, in order to provide maximum attack resistance.

This means that the different courts can have fees adapted to the tasks which they typically have to consider. The process of parameterizing new courts or updating the fees of existing courts goes through the Kleros Governance Process, and calculators that we have created to help inform these choices consider juror effort for the types of considered as a key input.

Notably, the values at stake in the case are not an explicit input into this process. So if a high-stakes case is nonetheless straightforward for Kleros jurors, it does not necessarily require higher fees than an equally straightforward, lower-stakes case.

Hence, as Kleros jurors receive fees in sources of external value (ETH or xDAI) and the price of PNK is not used in the calibration of fees, Kleros avoids the vicious/virtuous circle effects described above and the instabilities they can lead to.

In the remaining sections, we attempt to compare UMA and Kleros as they would exist if the markets using these systems were mature. In particular, one might expect that the subscription fees in UMA would be roughly equal to the total UMA tokens in a period created to pay rewards to voters. (At least, one would not expect that the tokens created would be more than a small multiple of fees so that the net inflation would be no more than a small constant rate.)

Spam

The choice that all voters vote in each call to the DVM also has important implications in UMA for fees and the potential to grief the system by creating spam cases.

Suppose that an attacker has an interest in an incorrect answer being provided to an upcoming question, and she decides to create spam questions to strain the system and make it less reliable while her question is being considered. Faced with an influx of questions, a UMA holder has the choice to

1. exert (some amount of) effort to consider the questions,
2. vote randomly or according to some other strategy that does not exert the effort to consider questions individually (such as always voting for the first option, etc), OR
3. not vote at all.

As voters in UMA do not risk losing a deposit if they vote incoherently, the strategy of voting randomly dominates the strategy of not voting all. (There is a caveat here that voters still have to pay gas, so this may not be quite true in an environment where gas is high relative to average rewards.)

We set some notation:

• As above we take F to be the total subscription fee required across the system for a unit of time and denote the percentage of the fee each contract must pay as :

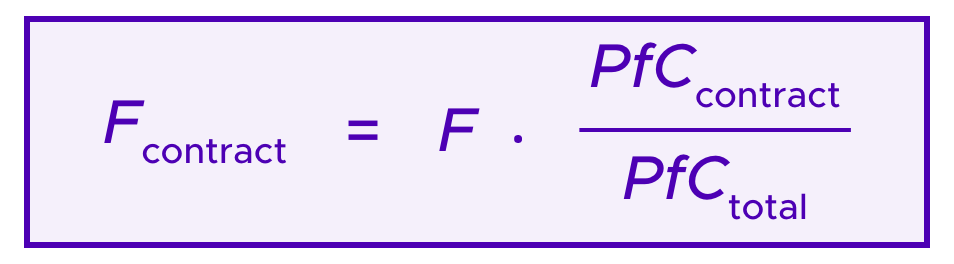
• Denote by N the average number of questions posed to the oracle per unit time.
• Denote by M the average number of UMA holders participating.
• Denote by e the effort required to evaluate a question.

If at least a given fixed, large percentage of UMA holders are willing to exert effort to consider the questions before voting, this requires an effort per question that scales as ~ M and a total effort that scales as ~ NM.

As we argued above, in a mature market, we expect that the total rewards paid to voters per unit time scales as ~ F. Then, each coherent participant receives a per-question reward on the order of ~ F/(NM).

If this reward is greater than the effort required, the spammer is providing value to the system. However, as we think of the effort e as being fixed, for sufficiently large M this will not be the case, so the attacker does e-O(F/(NM)) harm to the average voter performing effort. Then the total harm the attacker does is  Me-O(F/N).

Note that PFC_total is expected to grow with the number of contracts using the system. Then, if you expect that contracts require resolution by the UMA DVM at a roughly constant rate, this should be the same thing as scaling with the number of questions per unit time. Namely, PFC_total ~ N.

Then, this grief costs the attacker,

So, the attack has a griefing factor that goes as

Then, one has a dilemma where one needs to either:

1. Choose F that becomes large as N and M grow. If, for example, F ~ NM, then

So this causes the subscription fees to have to scale with the number of     participants making the system increasingly expensive to use if the UMA community grows. Alternatively, one can:

2. Accept the possibility that there will be spam griefs with large griefing factors where attackers can troll the the system, so that voters who do not vote randomly are overworked by the load of questions they need to answer, OR
3. Limit the use of the system to very simple questions where the effort e can be considered to be negligible. (For example, if the voters can be expected to have some software that draws information from some public data source and automates their responses.)

In at least some applications using UMA, there is the possibility for an admin to pause questions in the case of emergency. So this mechanism could be used by a centralized party to deal with such potential spam attacks. However, if the number of questions scales, it seems that it would also become more difficult to coordinate any decentralized governance process involving, for example, the UMA token holders around individually flagging contracts as potential spam. So it is not clear that this mechanism could offer a solution to the issue of potential spam that is both scalable and decentralized. Moreover, any system that tries to filter out spam questions before they go to the UMA DVM risks filtering out questions by honest actors as well which has the potential to be frustrating for users of legitimate contracts that require information.

In Kleros it is, of course, also possible to raise spam disputes. However, Kleros does not use a subscription fee model, and rather the full cost of the dispute resolution is paid to the arbitrator contract on a question by question basis. Then, these fees are parametrized to be large enough to incentivize each of the small number of jurors in an initial round to make an effort to study a case.

This philosophy of how to determine fees provides flexibility for applications integrating Kleros that only need to pay for the dispute resolution that they actually use. Moreover, it means that spammers pay for the full cost of the tasks they are imposing on Kleros jurors.

Parasitic usage

In blockchains, information typically circulates publically. This can pose challenges for oracle systems that require contracts to pay fees in exchange for the answer to a question such as Kleros and UMA. Indeed, if a contract pays fees to obtain the answer to a question, there is the possibility that a “parasite” contract that requires the same information will copy the answer it sees without paying fees.

In UMA, this problem is particularly relevant because of their subscription fee based model, where contracts with less value at stake pay less in fees. Then, hostile users can intentionally create proxy contracts that need a piece of information but have relatively little value at stake to call the oracle.

The UMA whitepaper details a proposal, that is currently not yet implemented, to deal with this issue via a zero-knowledge scheme. In the spirit of mixers, third parties can deposit money to the amount at stake that is distributed by the vote of the UMA holders. For example, suppose Alice and Bob have a dispute over 10 DAI in a registered contract with a larger parasite contract that requires the same oracle information, but where the dispute is over 100 DAI. Then Charlie can deposit 10 DAI into the contract with a cryptographic commitment that indicates that this amount should go to Alice. Then, during the resolution of the dispute Charlie can make interactive zero-knowledge proofs to UMA voters that this amount should indeed go to Alice; so if these voters think that Bob should win the underlying dispute they vote to award 10 DAI to Alice and 10 DAI to Bob. However, to the perspective of an outsider, this is indistinguishable from the situation where Charlies' deposit was on behalf of Bob and Alice won the underlying dispute. Thus, the parasite contract shouldn't be able to usefully process this information to resolve the larger dispute.

This is an interesting idea, though it is not obvious how to generalize it to less financial questions such as whether to include an entry on a curated list. Note that Kleros does not require advance registration of contracts in order to raise disputes, so contracts cannot artificially reduce their fees via this kind of attack.

Conclusion

UMA's economic guarantees are based around charging fees based on the value at stake in a case whereas the model of Kleros is calibrated around compensating jurors for the effort they have to perform to analyze cases. For Kleros this means that low-value, high-effort cases can be priced out from obtaining dispute resolution. For UMA, this choice creates a disconnect between the fees charged and the burden a question places on the system, creating thorny issues around spam and parasitic usage. Currently, UMA is managing to avoid some of these issues because its token valuation is high enough relative to the values at stake that the protocol estimates that it can set subscription fees to zero while maintaining security. However, these issues could become pronounced if the system matures to a point where token holders no longer have the same expectations that the system will continue to grow and fees are necessary to cancel the rewards so that the issuance of these rewards doesn't lead to substantial inflation.

As these issues become more severe for more complex questions, this reaffirms our earlier observations that Kleros is more appropriate for more complex questions, whereas UMA is more specialized for simpler questions that require strict guarantees on resolution time.