Uncommon answers: deposit sizes, lazy strategies, and peer prediction

The Kleros protocol has been designed to incentivize jurors to expend time and effort to analyze subjective cases that can sometimes be complex. In particular, it is important that the protocol penalizes "lazy strategies", namely juror voting strategies where jurors do not expend an effort to properly analyze a given case.
Lazy strategies can take a variety of forms. For example,
- A juror could vote randomly. In a dispute with two possible outcomes, this would mean that the juror had a 50% chance of choosing the winning outcome and being rewarded.
- A juror could also always vote for the same, fixed outcome. For example, suppose that one noticed that in a given category of curated list disputes, "Reject from the list" wins 70% of the time and "Accept in the list" only wins 30% of the time. Then a juror who just automatically votes for "Reject from the list" without bothering to read any evidence every time she is drawn in this type of case would, in the long run, choose the winning outcome and be rewarded 70% of the time.
Other more sophisticated strategies could also be possible fall in this category. One can even imagine edge cases where it is not clear if a voting strategy should count as a "lazy strategy" and be penalized or not. For example, a juror could design a very effective AI that took in the evidence and arguments of the case and produced a ruling.
If this AI is sufficiently well-designed, it could produce good rulings more reliably than some human jurors, so it may not be a problem to allow it to participate even though no human effort is expended to analyze cases when that juror votes. If one reached a point where jury panels are typically composed of some number of human beings and some number of AIs, then Kleros would be a sort of hybrid system depending on the decision making of both of these groups.
The main tool that is available in version 1.0 of the Kleros protocol to disincentivize lazy strategies is to adjust the following court parameters:
- feeForJuror,
- minStake, and
- alpha
In Kleros 1.0, the total amount of fees that are paid to jurors in a round with M jurors is M*feeForJuror. This amount is split among jurors whose vote agrees with the outcome of the final juror vote. In particular, if not all jurors in a given round cast votes that agree with the final juror vote, then each juror who does would receive more than feeForJuror.
The parameters minStake and alpha determine how much a juror who votes in a way that is incoherent with the final juror vote is penalized. Specifically, we say that this per vote penalty is given by:
voteStake=minStake*alpha.
When proposing parameter updates, typically we calculate feeForJuror and the components that go into the computation of voteStake as follows. For each court we need to make two estimations:
- p - the rate at which an honest juror would vote with the last round of juror voting
- t - the rate at which a dishonest juror following a lazy strategy could be rewarded by voting with the last round of juror voting simply by always voting for the most common outcome.
In practice when proposing parameter updates, we make these estimates by looking at historical data from the court. Specifically, we estimate p by taking the historical rate at which jurors are coherent with the last round of juror voting and we estimate t by taking the historical rate of the most common outcome winning.
If a court does not have enough historical data to make useful estimates, then one can try to guess values of p and t based on reasoning about how subjective cases in the court tend to be.
Then, one should choose feeForJuror and voteStake such that an honest voter who makes an effort that is valued at e and is rewarded at a rate of p should have a positive expected return:

while a lazy voter who does not make the effort to review the case and is rewarded at a rate of t should have a negative expected return:

For more detail on parameter calculation, see this blog article.
However, you will notice that this approach does not work very well if t grows too large. As it gets less and less likely that a juror pursuing a lazy strategy is penalized for voting for the wrong outcome, the deposit that she loses when that does happen has to be that much larger in order for her net expected return to be negative.
However, if the voteStake is large relative to the feeForJuror, this can cause a user experience problem for honest, risk-averse jurors. In an extreme example, imagine if t=.95. Then, a juror employing a lazy strategy is only penalized once out of every 20 cases, so one must have (at least)
voteStake>20*feeForJuror
in order to have E[lazy strategy]<0.
However, this will create very high stakes for jurors in this court as one mistaken ruling will have a very high cost. Even if p is also very close to one and a strategy of honestly evaluating cases has a positive expected return, the risk-return proposed by this court may not be acceptable to many jurors.
This raises an important question: in courts where some outcomes occur much more frequently than others, how can one incentivize jurors to take the time to review the case and vote for the uncommon answer if they believe it to be correct, without having unacceptably large deposits?
Among current Kleros courts, this issue is most acute in the Humanity Court where "Reject from List" wins around 85% of the time and deposit sizes have correspondingly become rather large.
Fees and deposits that vary based on outcome
One possibility to deal with these issues would be to have payments and deposits that depend asymmetrically on which option wins. The idea here is that if the option a wins much more frequently than option b, then one can just make the rewards and penalties for voting for option a less attractive so that the lazy strategy of always voting a becomes unprofitable.
Explicitly, one could have a payoff scheme given by:

where fa, fb, da, and db are parameters chosen by governance. Essentially, fa and fb are the fees that jurors receive for correctly voting for a and b respectively. Similarly, da and db are the voteStakes that juror loses as deposits for voting for a and b respectively if these options do not win.
Note that the Kleros 1.0 payoff system splits fixed arbitration fees between whatever jurors who vote for the winning answer in a given appeal round and furthermore redistributes lost PNK deposits from jurors who are penalized to those who are rewarded.
One could apply the idea of having different fees and deposits parameters for each possible outcome with such a redistributive approach and it offers similar advantages and disadvantages. For the sake of exposition, we will consider examples using this simpler model where the fees and deposits are not redistributed between the jurors.
How large do the amounts that users lose for incoherent votes need to be relative to what they can gain for coherent votes to disincentivize lazy strategies? In this simple model, a juror that employs the lazy strategy of always voting for the option a has a ta chance of receiving fa and a 1-ta chance of losing da. This gives her an expected return of:

Then, for this strategy to not gain money on average, one needs:
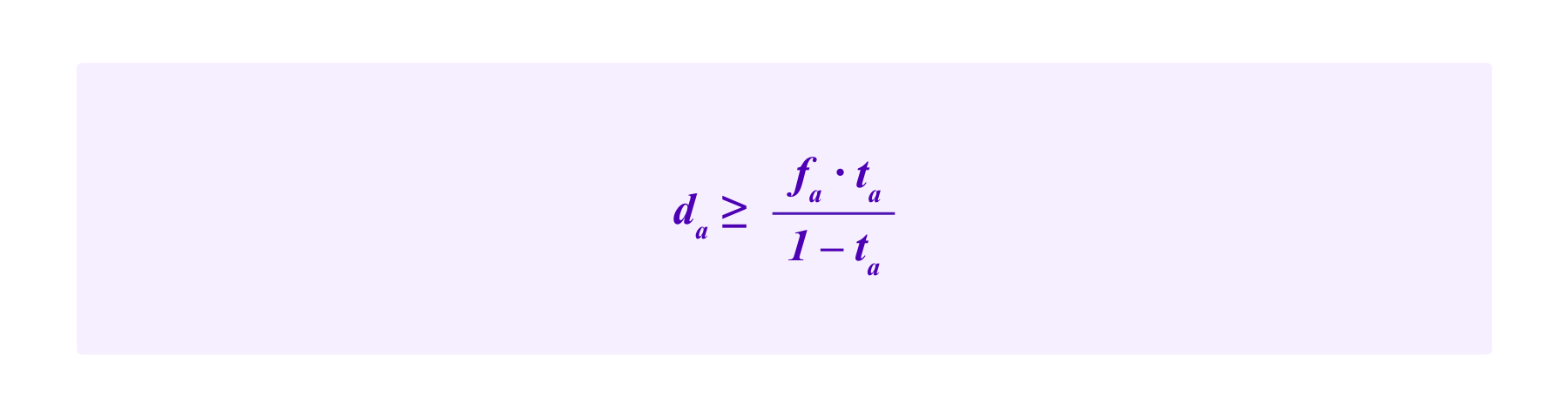
Similarly, if one wants the strategy of always voting b to not be profitable, one should have:

Furthermore, we would want the expected return of honest participation to be positive. Again we take e to be the value of the effort that the juror has to expend to evaluate the case and p to be the chance of coming to the correct conclusion conditional on making that effort. For the sake of simplicity, we assume that this chance of p of coming to the correct conclusion is independent of whether a or b is that correct outcome.
Then, on a given question, there is a ta chance that the correct answer will be a and a p chance that the juror will come to the conclusion that a is the correct answer. So there is a ta*p chance that the juror receives a reward of fa.
Similarly, there is a (1-ta)*p chance the juror receives a reward of fb for correctly voting for b, a (1-ta)*(1-p) chance that the juror is penalized da for voting for a when b wins and a ta*(1-p) chance that the juror is penalized db for voting for b when a wins. The honest juror expends the effort of e in all cases. Then, we want this total expected value to be positive:
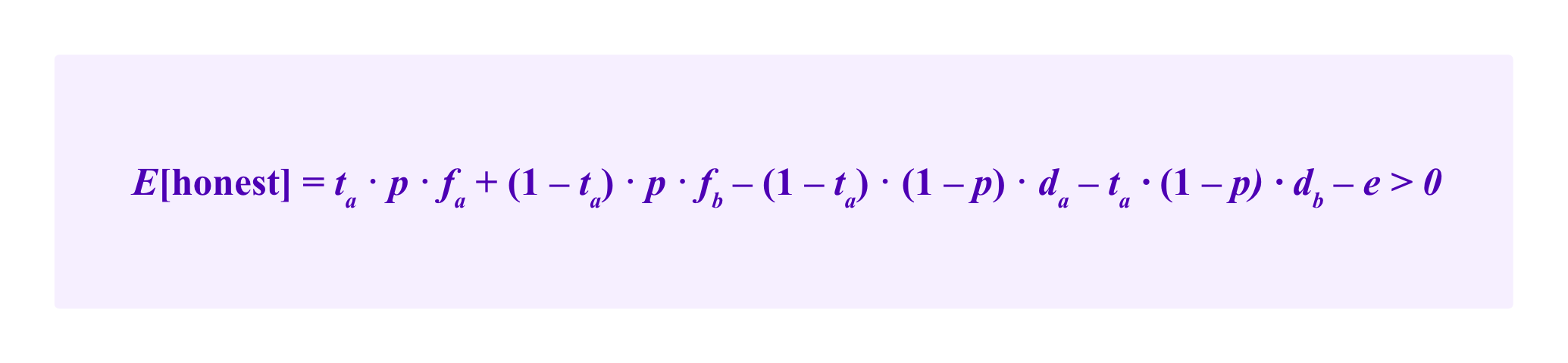
We noted above that, under the payoff scheme of Kleros 1.0, a category of disputes with t=.95 would require voteStake>20*feeForJuror to disincentivize the lazy strategy of always voting for the most common outcome. The same reasoning applies here: if ta=.95 then we need da>20*fa.
Now we might try to decrease fa so that da, the amount that a juror has at stake if she loses, doesn't need to be so large. Continuing the example where we assume ta=.95, hence tb=.05, suppose furthermore that p=.99.
Suppose we take fa=.5e. Namely, jurors who correctly vote for a are compensated for less than the effort they typically have to make to reach a decision; then fb will be larger than e so that in the long-run a juror will be rewarded enough from cases where b wins that her total compensation will justify her time and effort.
Then, we want
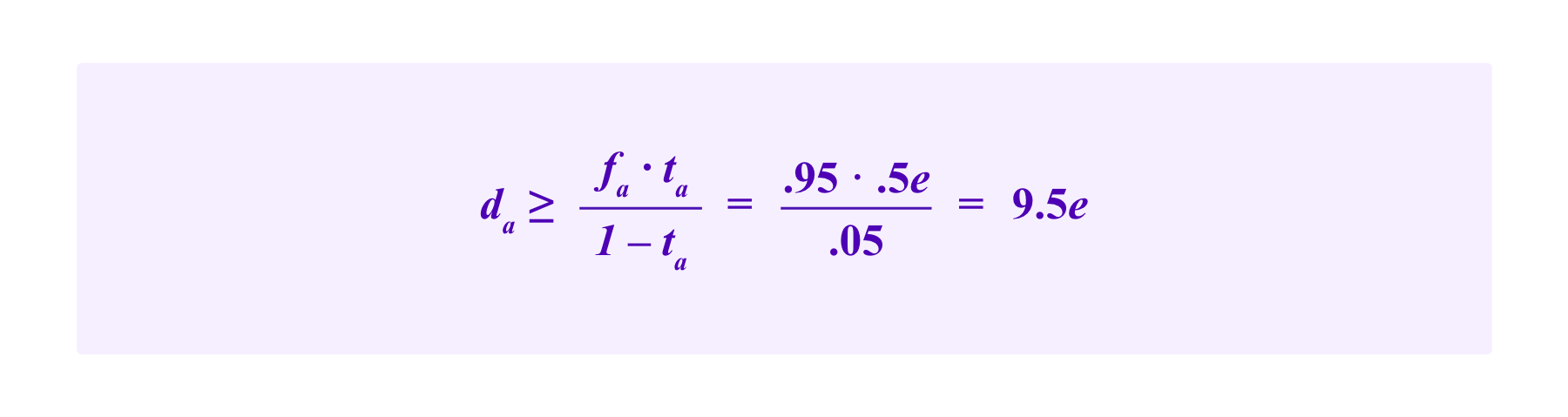
On the other hand, we compute:

where the second line uses the assumption that E[honest]>0 and the third line uses the condition above that prevents the strategy of always voting b from being profitable.
So we see that in order to reduce the amount that a voter who votes a can lose by roughly half we need to pay jurors who correctly vote for option b roughly 10.8 times the effort that they make per case so that the total compensation is sufficient.
In some courts, depending on the jurors' preferences for risk aversion, this might be an acceptable payoff structure – jurors who vote with the majority receive .5e when that majority outcome is a and they receive 10.82e when the majority outcome is b.
However, this raises important technical questions. How much must the parties to the dispute pay upfront in arbitration fees? In the arbitration standard used by Kleros, arbitrable contracts are expected to pay the maximum amount of fees that could be required for their case in advance to the arbitrator contract.
Moreover, the current Kleros smart contracts are not well setup to issue refunds of excess dispute fees to the parties. Indeed, in the edge cases present in Kleros 1.0 where jurors do not receive the full amount of dispute fees, the excess is just sent to the Kleros governor contract.
Thus, a naive approach of requiring parties to disputes to pay upfront significantly more than the typical effort to resolve their case, in this example 10.8 times the value of that effort, just to cover (relatively uncommon) cases where the payout needs to be higher without the possibility of having the difference refunded in other cases is clearly not viable from a cost perspective for these parties.
Instead, one could imagine an approach where the party to the dispute puts in fees corresponding to the average of what jurors need to be paid for that category of dispute over the long-run. In the example, this average corresponds to paying out .5e per juror in 95% of cases and 10.8e the remaining 5% of the time for an average amount of .5e*.95+10.82e*.05=1.02e per juror.
Then, if the option a wins the case, the arbitrator contract already has enough funds locked up to pay .5e to each juror and send the remaining .52e to the governor contract. If b wins, then the jurors who vote for b can receive 1.02e directly from the arbitrator contract. The remaining 9.8e that they should receive to be properly incentivized can be airdropped to them periodically from the amount that has accumulated on the governor contract from the cases where a won.
This approach could be viable, though notice that it would be important to calibrate the parameters well so that the amounts the governor has access to cover its expected payouts. Notably, one might worry about accumulated funds on the governor becoming a target for potential attacks. In Kleros 1.0, the payments for each case are essentially independent. This limits the degree to which issues in one case can cause problems for others.
Lessons from peer prediction
These problems are related to those studied in the academic field of peer prediction. Papers in this field consider a set-up similar to that of Kleros; one attempts to design an incentive system to encourage users who are voting on the correct answer to some question to respond correctly.
However, a typical feature of peer prediction systems that is not present in Kleros is that users are required to provide percentage values for the rates at which they think the other voters will answer each outcome.
These percentages provide the system with additional information that can be used in a variety of ways. One interesting idea due to Prelec that is present in some peer prediction systems is to reward "surprisingly popular" answers. If 45% of users vote for answer a, but the average user predictions that only 35% of votes will go to a, then a is given extra weight by the system beyond just its 45% of votes.
The idea is that users with some expertise on the question will provide the correct answer, but expect other to vote for some other plausible but incorrect alternative. The presence of this category of expert users that votes for the correct answer a but attributes a low percentage of other users doing so manifests itself in a discrepancy between the predictions for that answer and its ultimate rate of votes.
A famous example of this idea is to ask individuals to name the capitals of US states. Voters who know that the capital of Pennsylvania is Harrisburg might expect less informed voters to vote for Philadelphia. Meanwhile, voters who think that the capital of Pennsylvania is Philadelphia will expect other voters to also vote for Philadelphia.
Thus, the predictions given by voters attribute a high rate of votes to Philadelphia and a low rate of votes to Harrisburg. As there are nonetheless some informed users who vote for Harrisburg, Harrisburg may be seen as a "surprisingly popular" answer.
A concrete example of a peer prediction system is that of the Robust Bayesian Truth Serum (RBTS). In that paper, we assume that each voter i submits a vote of the form vi, yi where vi is the alternative that i believes should be the outcome of the decision and yi is a set of percentages that predict the breakdown of votes for each of the possible votes, e.g. yi(a) is the percentage of voters that i expects to vote for the alternative a.
Then, in order to determine the payoff for i, she is randomly paired with a peer î. Then her rewards are given by:

The first term here:

is called the "information score" and is designed to measure the quality of i's vote vi. Here,
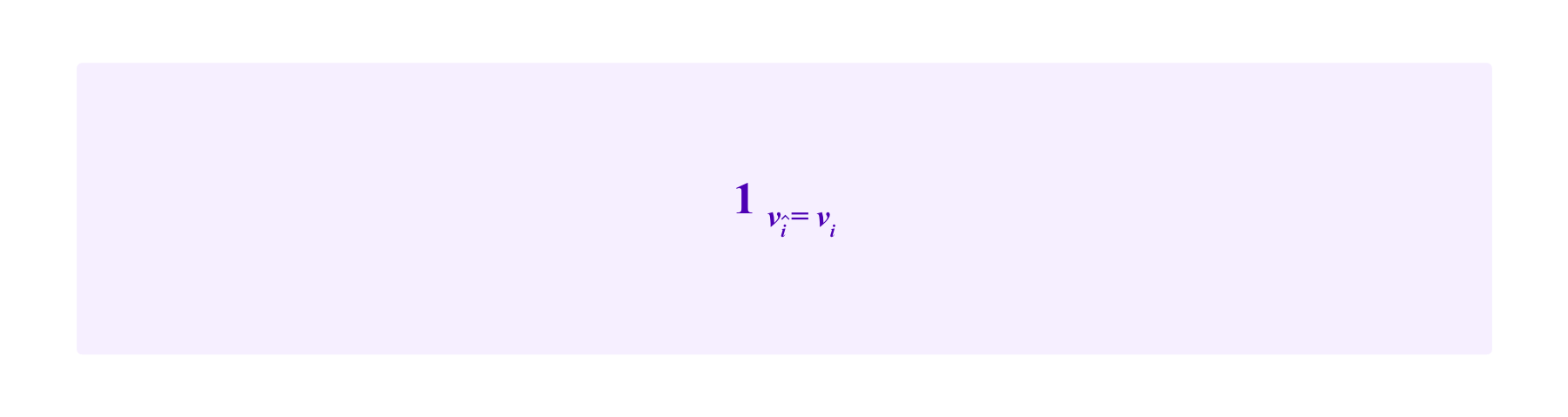
is the indicator function that is 1 if vî=vi and is 0 otherwise. Thus, i receives a positive value for her information score only if her vote agrees with that of î.
While Robust Bayesian Truth Serum as it is presented by Radanovic and Faltings differs somewhat from Kleros in that RBTS compares voters' answers to specific peers rather than the collective winning answer, the basic principle is the same. You are incentivized to vote for answers that you think other voters will also vote for because they seem natural and distinguished, thus increasing the probability that you have a positive information score.
However, note that the indicator function here is weighted by a factor of 1/yî(vi). Namely, conditional on the votes of i and î agreeing, the less likely î thinks vi is to be voted by other users, the more i is rewarded for voting it.
The second term:

is called the "prediction score" and is designed to measure the quality of i's predictions yi. Here R(yi,vî) is a strictly proper scoring rule.
For example, one can take R(yi,vî) to be the quadratic scoring rule:
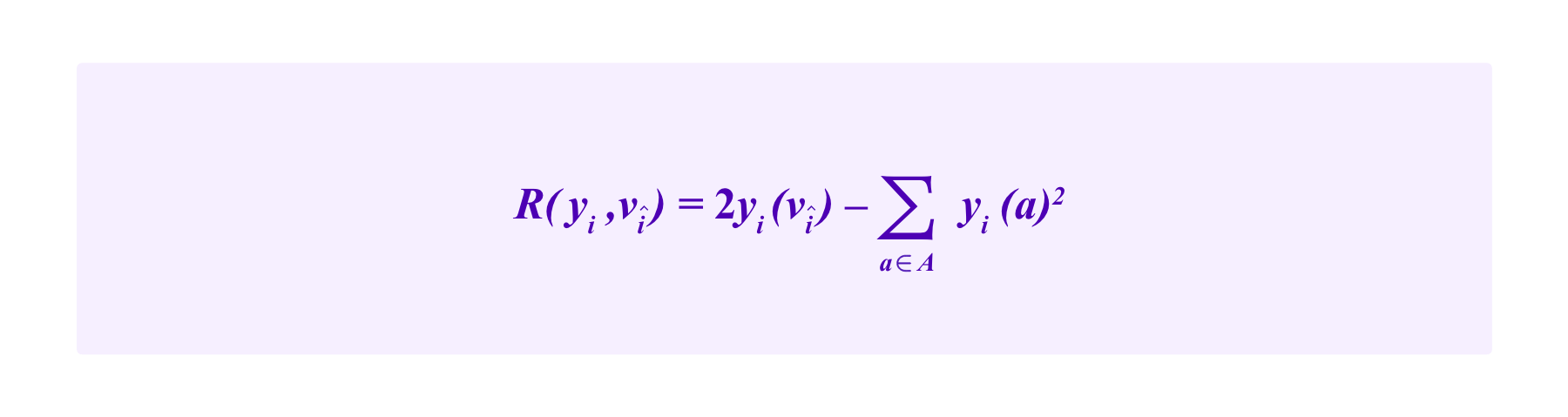
Then the expected value of R(yi,vî) is given by
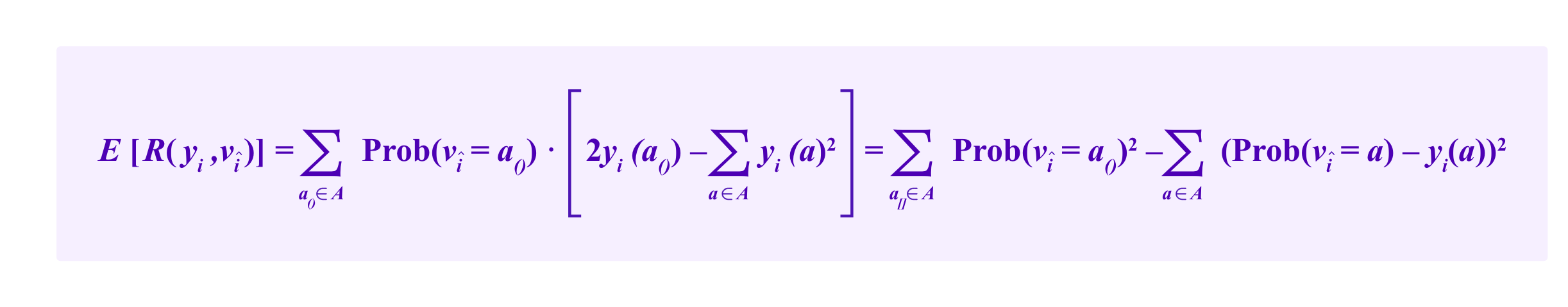
which is maximized yi(a) exactly is equal to Prob(vî=a) for all a. Thus, i is rewarded for predicting the distribution of votes as accurately as possible.
One thinks of each user observing one possible outcome as the truth; we write Si=a to denote when the user i observes the outcome a. Moreover, each user makes some probability estimates for how the other users will vote given her observation, e.g

is the probability from the point of view of i that the user k will vote for a assuming that i observes b as being the correct answer.
Then, in Radanovic and Faltings, it is shown that if one has
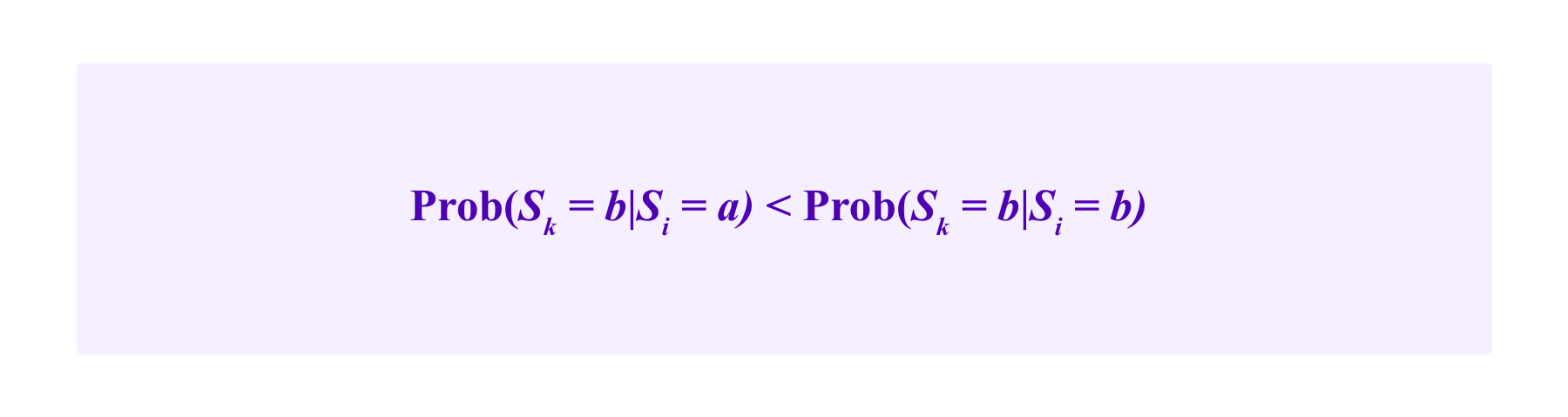
for all users i and all alternatives a , b that are not equal, and one makes reasonable assumptions on the independence of the probability estimates conditional on the observations made (notably this model assumes that users do not collude – we will get back to this assumption below), then users are incentivized to vote for their observation.
This is true even if there are a and b for which
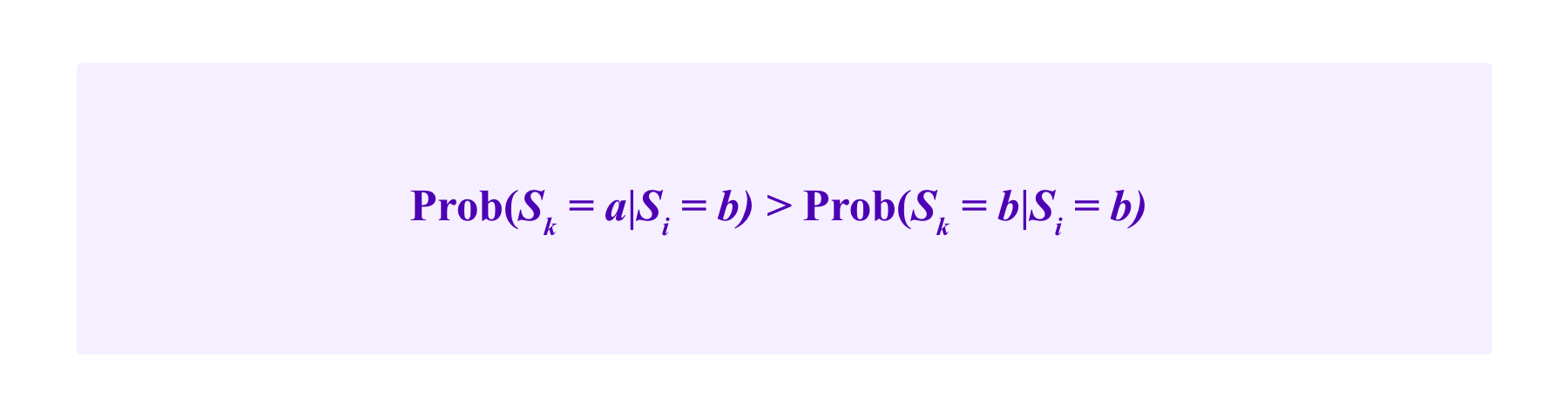
Namely, i might have such a strong prior belief that the option a almost always wins that even if she observes b as being the right observation she still thinks that it is most likely that other users will observe a. Even in this case, as long as observing b makes i more likely to think that b is the truth than if she hadn't observed b, RBTS is capable of incentivizing users to vote for their honest observation.
This is a related problem to our discussions above about incentivizing jurors to vote for options that are only rarely selected as the honest outcome. Here the goal is to incentivize jurors to vote for even the most uncommon outcomes if that is their honest observation, which is not exactly the same goal as being able to incentivize jurors to vote for (relatively) uncommon outcomes at user-friendly parameter choices. Nonetheless, one might hope to be able to adapt some of these ideas.
Note that these ideas can have limitations. An issue with applying the types of peer-prediction schemes discussed above in a blockchain setting is that the results one can prove about their incentive-compatibility typically assume that voters are not capable of colluding, and they have issues when these assumptions do not hold. A subset of voters can pretend that an option is surprisingly popular to make themselves seem like particularly well-informed voters and extract disproportionate payments.
In the RBTS scheme, a pair of colluding voters (or a user that has managed to get two votes) could observe a case where she thinks that honest voters would tend to vote 67% for a and 33% for b. Then, rather than submit honest predictions, she might use her two votes to vote b and provide predictions that 90% of voters will vote a and only 10% will vote for b.
If her two votes are not paired together and instead she is paired with honest participants, the attacker would receive a lower prediction score than if she had made honest predictions. However, if the two attacker votes are paired together, her information score would be 1/.1=10 rather than the 1/.33=3 she could obtain by participating honestly.
These issues are particularly pertinent in a blockchain setting as blockchain identity tools are limited, and blockchain systems are typically only able to make it expensive rather than impossible for participants to obtain multiple votes. Some more recent research has considered peer-prediction type ideas that are resistant under attack models that correspond to blockchain environments.
Recall that the modular structure of Kleros 2.0 allows for using different voting and incentive schemes as one progresses through the appeals of a given case. Thus, one could use a scheme based on peer-prediction ideas in early appeal round(s) for a case, and then default back to something more attack resistant in later appeal rounds.
This would be in line with broader design principles in Kleros that the attack resistance of the system is mostly based on the appeal system. If a decision on a valuable case is made by only a few jurors, an attacker can gain a lot of influence by just managing to bribe a handful of individuals. Moreover, there will always be the chance that a small panel of only a few jurors will produce an idiosyncratic outcome just because the random jurors selected are non-representative.
On the other hand, if one uses peer-prediction ideas to better handle cases where outcomes win at unbalanced rates, this is likely to only be necessary in early rounds anyway. Indeed, if a case is appealed, it is usually because multiple outcomes are plausibly defendable. Then, if one uses the Kleros 1.0 payoff rule, it should not be necessary to have particularly high deposits for lazy strategies to be unprofitable in appeal cases.
Using peer prediction to judge severity of erroneous rulings
An idea that we have considered to adapt the above ideas from peer prediction is to have a similar setup where participants submit a vote and a prediction which are evaluated by an information score and a prediction score respectively, where the information score now is given by:
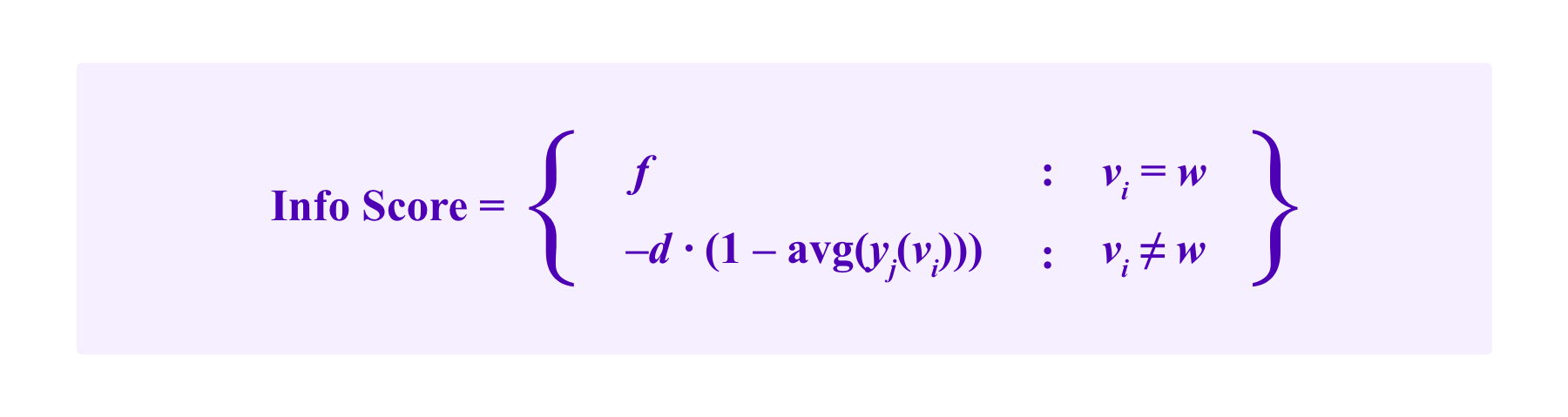
for choices of fees f and deposits d determined by governance, and where w is the winning outcome. The idea here is that the average of the predicted rate of voting for a given by the peers, avg(yj(a)) for any given possible outcome a, gives a sense of how clear-cut the dispute is.
Then this function gives i a score that does not penalize her too severely if
- the alternative that i votes for does not win, but
- the average peer predictions for that alternative are relatively high so the other users believed that that outcome was plausible.
This approach is based on the observation that many disputes will not be particularly contentious and that jurors will be able to choose the correct outcome with high probability and expect other jurors to do the same. Then an honest user will only be attributed the lowest information scores if she votes incoherently despite the other participants believing that the case was clear-cut, which should be relatively rare.
Meanwhile a lazy voter who is trying to implement an automated strategy based on making little or no effort to review the evidence of the cases will make errors on cases where it would be very rare for an honest juror to have made a mistake. In these situations, the lazy voter receives the largest possible penalty.
In the full payoff rule, we should also include the prediction score. Note that a lazy strategy that could obtain a good information score by always voting the most common outcome a may or may not be capable of also obtaining a good prediction score depending on whether the rates at which jurors vote for a are also as predictable or not.
For the sake of simplicity in our examples below, we will will only consider the information scores for the payoffs in the peer-prediction system and ignore the prediction scores for the moment. Ultimately, the prediction score is, of course, critical in incentivizing participants to provide predictions which can robustly be used in the calculation of the information score.
Then, as an explicit example, again suppose we have a category of binary cases between a and b. Suppose that 90% of these cases are clear-cut and any juror who takes the time to thoroughly review the evidence will vote for the winning answer with 99% probability. In the remaining 10% of cases, we suppose that the evidence is more mixed, and a juror who thoroughly reviews the evidence will only vote for the winning answer 60% of the time.
On the other hand, suppose that the answer a is the most common answer across all of these disputes, winning 89% of clearcut disputes and 50% of non-clearcut disputes.
Note that one would not necessarily expect the rates at which the most common answer wins to be the same for both the clearcut disputes and the disputes with more mixed evidence. Indeed, in the subset of cases where the evidence is very borderline, you wouldn't expect one outcome to win that much more frequently than the other.
Then the total rate at which a wins is:
.9*.89+.1*.5=.851
and the rate at which an honest juror making an effort valued at e to review the cases would vote for the winning outcome is:
.9*.99+.1*.6=.951
Thus, this gives the t and p values, as we have defined them above, respectively.
We now calculate the expected returns of honest jurors compared to jurors who always vote for a, using the peer-prediction scheme described above and also using the payoff system in Kleros 1.0.
Suppose all users honestly review the case and provide corresponding votes and predictions scores except one lazy juror who always votes for a. There is a .9*.99 chance that the case is clear-cut and an honest juror selects the right answer and a .1*.6 chance that the case is not clear-cut, but the juror select the right answer anyway for a total of a .9*.99+.1*.6 chance that the honest juror is rewarded f.
There is a .9*.01 chance that the case is clear-cut but the honest juror is wrong. In this situation, the other honest jurors will have given predictions of yj=.99 for the winning outcome and yj=.01 for the losing outcome as they perceive the case to be clear-cut. So the juror who votes incorrectly is penalized (1-.01)d.
Similarly, there is a .1*.4 chance that the case is not clear-cut and the honest juror is wrong. In this situation the other peers would have estimated that the option she votes for would nonetheless have 40% support. So the incorrect juror is penalized (1-.4)d.
We put this together to calculate the expected information score of the honest juror, again deducting the effort of e that she spends to evaluate the case, as follows:

Similarly, the lazy juror has an expected information score of:
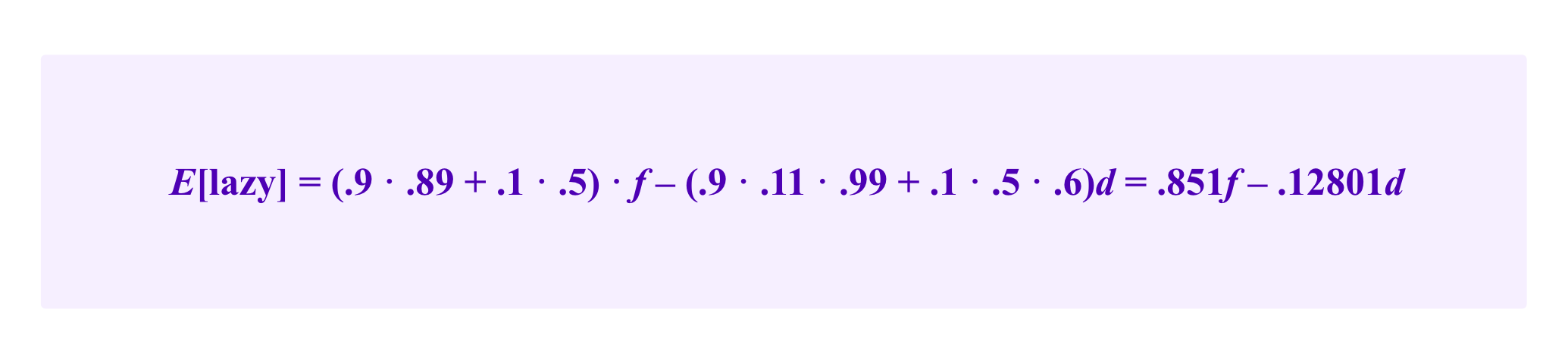
Then, if one wants to calibrate f and d such that
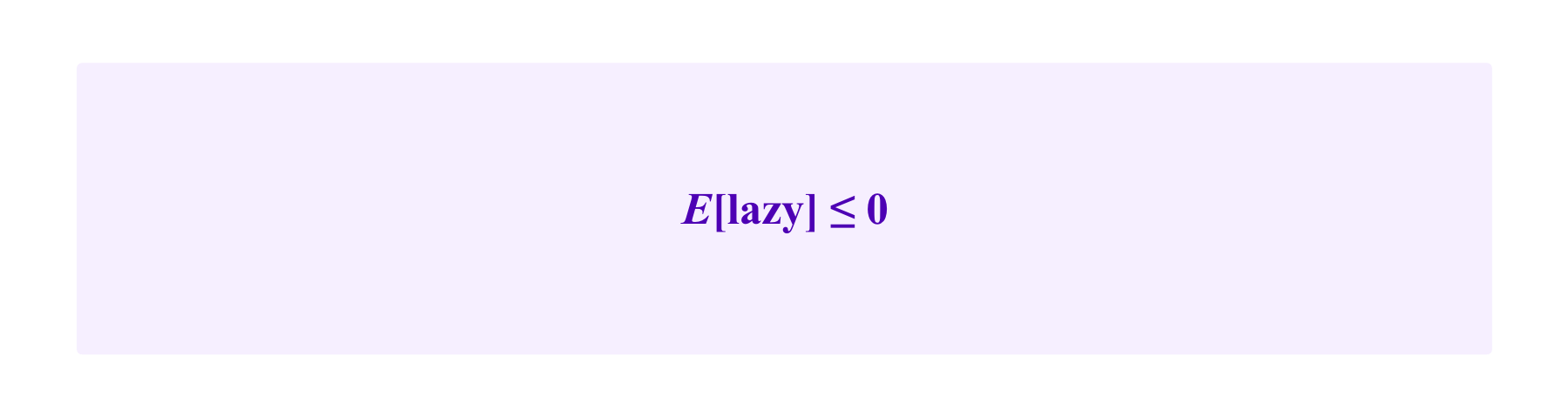
one must have
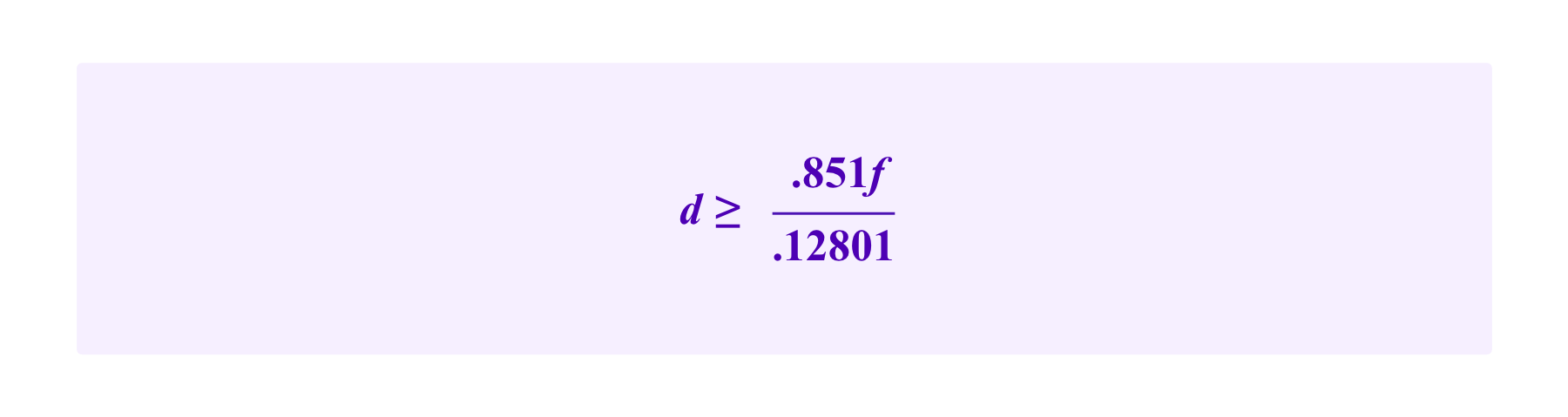
If we further want

then we must have
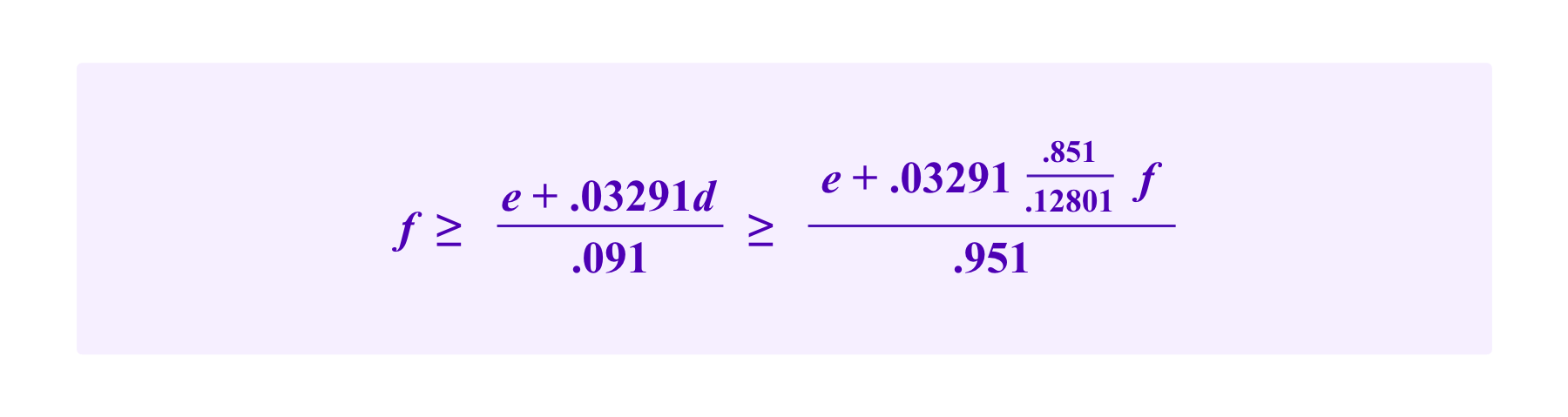
Thus, we see that the smallest values of f and d that satisfy these inequalities are f=1.37e and d=9.08e.
Compare this to the returns they would have if we just rewarded all jurors who vote with the winning outcome f and penalized incoherent jurors by d without using incorporating these peer predictions:
E[honest]=.951*f-.05d-e
and
E[lazy]=.851*f-.149d.
Then, if we similarly want

we can perform similar calculations to see that we must have

Then the smallest values of fees f and deposits d that satisfy these inequalities are f=1.50e and d=8.58e.
Thus, by incorporating the peer predictions in this way, we have actually raised the required deposit slightly from 8.58e to 9.08e. On the other hand, in the Kleros 1.0 scheme, honest jurors lose the full deposit much more often in the peer-prediction scheme.
Indeed, in this example, with the payoffs of Kleros 1.0, jurors lose the full deposit of 8.58e in 5% of cases whereas in the peer-prediction scheme jurors are penalized .6d=5.49e in 4% of cases and .99d=8.99e only 0.9% of the time.
Essentially, the peer-prediction payoff scheme is more efficient in penalizing lazy voters than the Kleros 1.0 payoff scheme for given deposit sizes. In the expected value calculations above, the terms that correspond to the juror being rewarded (+.951f for honest jurors and +.851f for lazy voters) are the same in the Kleros 1.0 payoff scheme and in the peer-prediction scheme.
However, in the peer-prediction scheme the term that corresponds to the juror being penalized is -.0329d for honest jurors and -.12801d for lazy jurors. This gives a ratio of .12801/.0329=3.89. In contrast, in the Kleros 1.0 payoff scheme, the penalty term for honest jurors is -.05d and the penalty term for lazy jurors is -.15d for a ratio of .15/.05=3.
Another way of looking at this is to consider ways to explicitly consider risk aversion in the utility functions of participants. A standard way of doing this is to weight rewards and penalties differently, applying a multiplier to losses:

Then, Ⲗ>1 corresponds to a participant being risk averse. Namely, if such a user has a 50% chance of gaining 1 euro and a 50% chance of losing 1 euro, her expected value is
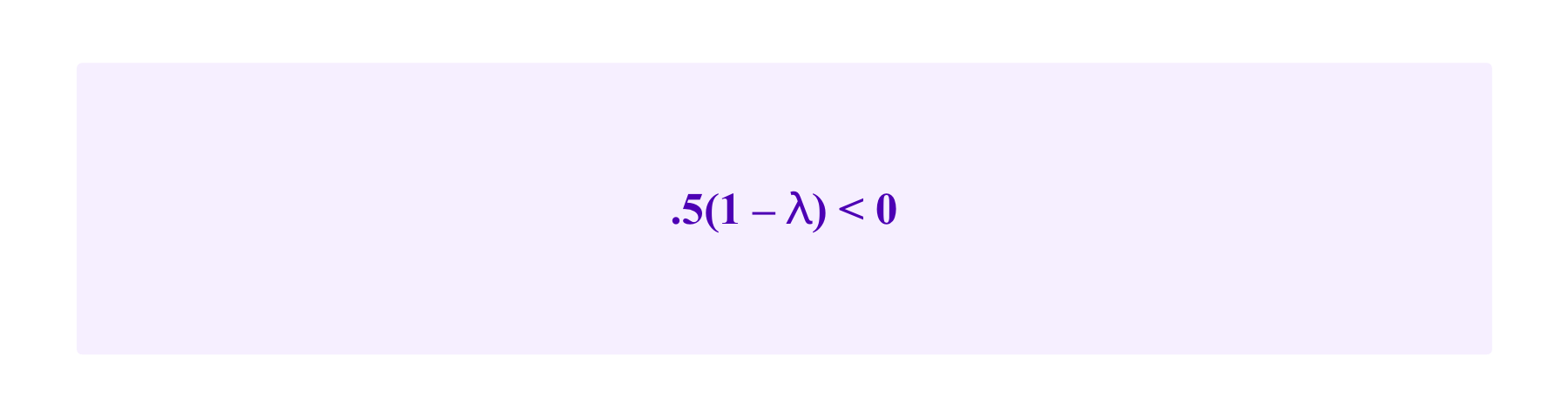
Then, the expected utility functions of the honest users in the example above adjusted in this way for risk aversion are

using the peer-prediction payoff scheme and

and using the payoff scheme of Kleros 1.0.
Note that both of these expected values are roughly equal to 0 when Ⲗ=1 because, in this example, we have chosen f and d so that the total average return for honest participation for a risk-neutral juror compensates the effort that she makes.
On the other hand, note that as one takes larger values of Ⲗ, the adjusted expected value of honest participation is higher under the peer prediction scheme than under the payoff scheme of Kleros 1.0.
Putting ideas together and other approaches
Note that the two approaches we have discussed, having fees and deposits that vary based on the outcome of the dispute and using peer-prediction tools, can be put together. This could give a payoff rule that looks like:
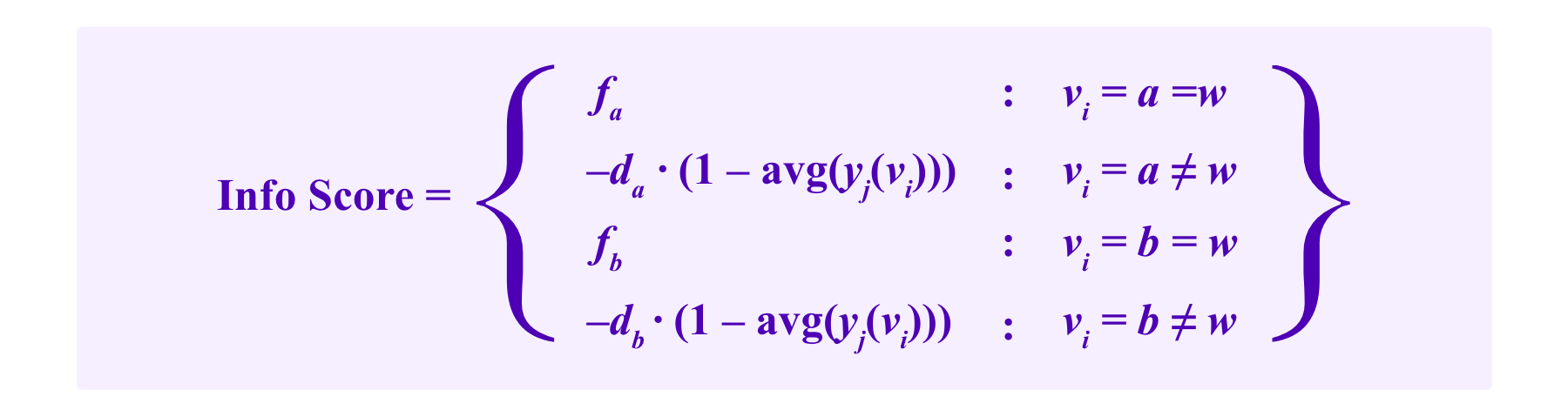
Here, again, fa and fb represent the fees that one receives for voting for the options a and b respectively if that option is equal to w, the winning outcome. Now the stake that jurors lose if they vote for an option that does not win is given by da or db, depending on whether the juror voted for a or b respectively, which in either case is multiplied by a factor involving the average peer-prediction of the rate of that outcome avg(yj(vi)) to give the system information on whether the case was clear-cut or not.
Thus, one could attempt to calibrate so as to have the advantages of both approaches while limiting their drawbacks.
Moreover, recall that this entire discussion has been motivated by how to make sure that jurors are disincentivized from voting without spending effort to analyze the details of the individual cases before them. We have focused on making sure that the payoffs that they can receive are such that the amount that they can improve the accuracy with which they answer questions by spending the time to look at the case is the difference between being able to participate profitably or not.
However, another approach is to change the nature of the task of the juror in such a way as to make it more obvious when a juror is not making the effort to analyze the individual cases. In Kleros 2.0, we have considered having a mechanism where, at least in some courts, jurors will be required to act according to certain guidelines.
Then, if a challenger notices that a juror is not following these guidelines, the juror can be challenged creating a dispute in a new “Juror Misbehaviour Court”. For example, jurors can be required to provide a reasoning justifying how they voted and jurors who fail to do so can be penalized by this mechanism.
In Kleros 1.0, jurors have the opportunity to provide justifications for their votes and they are incentivized to do so insofar that these justifications are seen by jurors in eventual appeals. A juror would want to convince these appeal jurors of the correctness of her vote as it is the final juror vote decided by the last appeal that determines whether the juror is rewarded or penalized.
However, the mechanism based on the Juror Misbehaviour Court provides a more robust requirement for jurors to provide justifications. The modular structure of Kleros 2.0 has been designed so that this structure can be added as a module at some point after the new version of the court has been deployed.
Then, note that it is significantly more difficult for a juror to vote without considering the evidence of a specific case if she is required to provide a justification of her vote. Thus, this mechanism can already help to address this issue in certain cases.
Conclusion
Kleros 2.0 is designed to offer more modularity so that one can adapt different mechanisms to courts and categories of cases with different requirements. This flexibility should allow for better, more tailored user experience. In this article, we have particularly examined some ideas on how one might improve the risk that potentially risk-averse jurors take on while participating in Kleros.
These ideas, while each having their drawbacks and limitations, can make sense in some Kleros courts, particularly for early rounds of cases. Then, one can expand the universe of disputes for which Kleros works smoothly to even include disputes where some of the voting options almost never win, nonetheless incentivizing jurors to vote for those outcomes when they believe them to be the honest choice.

