Smart Contract Price Oracles - The Best Approach?

Price Oracles?

Blockchain oracles are a key part of decentralized applications. In blockchains, code is law, but most of the time, you need real-world dynamic data to apply the law with. This is where oracle systems come in. They allow us to bring real-world data into our smart contracts in a decentralized and trustless way, bridging the gap between blockchain and real-life. Price/Linear oracles are just oracles that are optimized to work with discrete linear values like the price of a currency pair or the temperature at a given location at a given time.

Previous Work

Last May, we published an article on some research we were doing on how Kleros could be used to implement linear oracles. The gist of it was that parties submit ranges that they believe a given value falls into, e.g. the price of ETH in USD, we take the median of the points of incoherence of these ranges, and raise a dispute asking jurors whether the true value is higher or lower than this median. The process can then be repeated with the set of ranges that won, recursively, until an answer of sufficient accuracy is reached.

You can look at it as a sort of binary search with complexity that scales with the log of resources of the parties that are ruled to be wrong. You can read William’s, our cryptoeconomics researcher, analysis here, https://medium.com/kleros/the-oracle-of-the-kleroterion-c8eac7c10401. It’s a very cost efficient process, but could potentially take large amounts of time depending on the lifetime of a dispute in the subcourt that handles them.

A Better Approach?

After a long day of smart contract reviews, Clement was waiting for Uber Eats to deliver his favourite, Indian food, and I was about to head home, and I asked if the research on the linear oracle protocol was advanced enough to try developing a first version of the contract. He misunderstood what I said, he thought I was talking about partial order sets, paused for a minute, and stood up with a lightbulb look in his face. I was confused and had no idea where he was going with this. After a few minutes of doodling on one of the office’s whiteboards, I started to see what he had come up with and put my bag down with excitement.

A Rundown on Types of Orders

In case you are not familiar with order theory, here is a brief rundown. So, the two most common orders are total and partial orders. Total orders are your classic, simple, line up numbers on a timeline, order. Partial orders are a bit more complex. We can define them formally with 4 properties. Note that `<=` does not imply less than or equal, it can represent any one-way binary relation.

1. Asymmetry: If `a <= b` and `b <= a`, then `a = b`. In other words, two elements can’t be related in both ways.
2. Transitivity: If `a <= b` and `b <= c`, then `a <= c`. In other words, if an element is ordered before another element and that other element is ordered before a third element, then the first element is also ordered before the third element.
3. Connectivity: `a <= b` or `b <= a`. In other words, two elements must be related in at least one direction.
4. Reflexivity: `a <= a`. In other words, an element is always related to itself.

With these we can define:

• Total orders as having at least properties 1, 2, and 3.
• Strict total orders as having at least properties 1, 2, and 3, and not 4.
• Partial orders as having at least properties 1, 2, and 4.
• Strict partial orders as having at least properties 1 and 2, and not 4.

Now, back to our Oracle. The relation we care about is the one that makes two ranges incoherent. We can define this as, “Range A is ordered before range B, if all elements of range A are less than all elements of range B.”. This means [1-5] <= [6-7], but [1-6/7/8/9…] is not <= [6-7]. In English, if sets overlap they are compatible, otherwise they are incoherent and one comes before the other. It turns out that this relationship is an example of a strict partial order, and this has some nice properties to it.

Leveraging Partial Ordered Set Trees

Say we have this list of ranges:

1. [1-3]
2. [2-4]
3. [3-5]
4. [6-7]
5. [8-9]
6. [10-11]

Now, ordering them using the relationship we just defined, would give you something that looks like this:

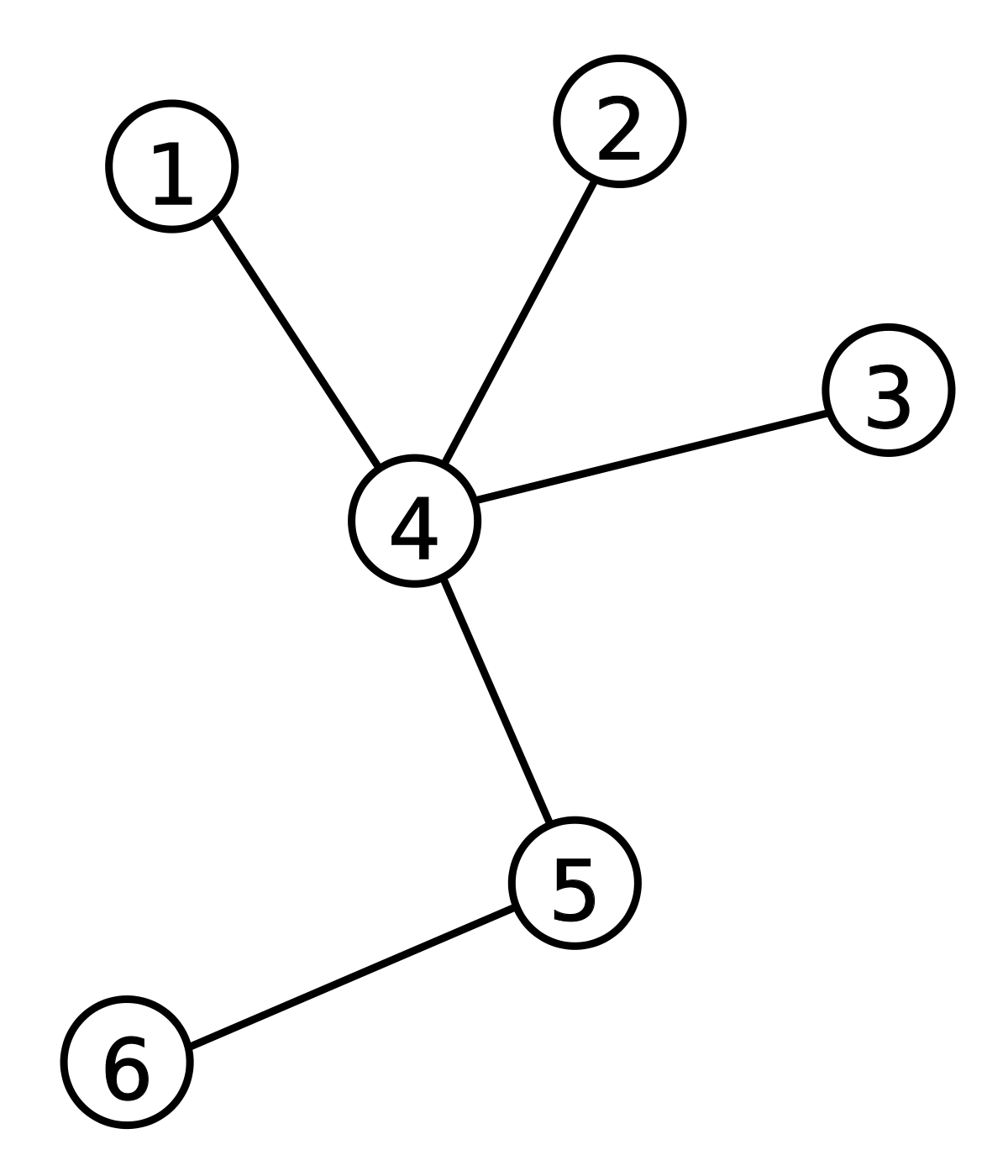
This has a very nice property. If you look at how things are ordered, you will see that every edge represents a point of incoherence. So, how is this useful? Well, we can now perform a really nifty algorithm:

1. Raise a dispute on every edge, grouping compatible ranges. In our example that would be (nodes 1, 2, and 3 vs. node 4), (node 4 vs. node 5), and (node 5 vs. node 6). Jurors should rule in favor of the side they believe is the most accurate.
2. Eliminate all nodes that lost a dispute.
3. If there is more than one compatible set remaining, then you can start again from step 1, otherwise, the union of all remaining nodes is your answer.

 This means that with reasonably honest jurors we can get the answer in one round of parallel disputes, making the time to find an answer constant at the price of a not so significant increase in arbitration fees due to the potentially higher amount of disputes.

Building the Trees Efficiently

We ran some preliminary tests to see if this algorithm works on various combinations of ranges and it appears to be sound and complete, but we were still worried that building the tree would be too computationally complex to do on-chain. So I pulled out a little REPL and started playing around to see if I could get it down to at least O(n) complexity, and I did. If you require range endpoints to be inserted into an input list in order, always breaking ties with an opening endpoint rather than a closing one, like so:

You can then build the partial order tree like this:

This is javascript by the way, and you can pretty print the result with this:

Run the whole thing yourself here, https://repl.it/repls/CalculatingCorruptGigahertz.

Future Work

So, now that we have a viable implementation of this, it looks like our Oracle research is only beginning. The next step will be to try to formally verify the algorithm. If it checks out, we can start to work on a paper and implementation. It’s exciting to work in a field like this where so much is still left to be discovered and created, and old mathematical work can power exciting new real-life applications. Who knows what other things can be optimized with something as old as order theory.

Connect with Us!

 Join the community chat on Telegram.

 Visit our website.

 Follow us on Twitter.

 Join our Slack for developer conversations.

 Contribute on Github.