Research Topics in Kleros Juror Selection Part 2 : Spectral Clustering using Soulbound Tokens

Soulbound Tokens are an idea introduced by Ohlhaver, Weyl, and Buterin to enable a social, non-financial layer in blockchains. Individuals are awarded non-transferable Soulbound Tokens (SBTs) that attest to their on-chain experiences and perhaps aspects of their off-chain identity over time.

We discussed some ideas about how Soulbound Tokens could be used in Kleros juror selection in a previous post. We will briefly review some of the key elements that we will need here before analyzing a specific juror selection method that uses SBTs.

Nonetheless, it might be helpful to re-read that article to recall the broader context of how we imagine SBTs interacting with Kleros, including discussions on how SBTs might be distributed as well as brief discussions of various different possible mechanisms that could use them in Kleros juror drawing, before digging into this post.

Recall that we wanted to use the social information from Soulbound Tokens to attribute potential jurors to groups based on their social characteristics. Then the idea is that by giving extra weight in the drawing process to jurors from less common groups,

• one can form a panel of jurors that can draw upon different backgrounds and experiences. Social science research has shown that diverse decision making groups can often produce higher quality decisions that homogenous groups, even when the members of the homogenous groups are individually higher performing.
• if the mechanisms that attribute SBTs are robust, it becomes that much more difficut for an attacker to gain enough weight to obtain half of the votes on a given case. The attack resistance model in Kleros 1.0 is based on an attacker needing more than 50% of staked tokens to be able to reliably receive half of the votes in the Kleros General Court – while this type of economic security already gives the court a certain level of defense, if the attacker simplfy cannot obtain a drawing weight of 50% even if she manages to buy enough PNK because she lacks the identity characteristics she needs to get relevant SBTs, the court is that much better defended.

Note that the modular structure of Kleros 2.0 allows one to use different drawing mechanisms for different categories of cases, and indeed to gradually add new mechanisms over time as research progresses.

When doing this research, we generally take the perspective that the various defenses of the court should be complementary. If any given defense breaks, it should still be difficult for the attacker to take over the court as long as the other defenses remain robust.

If the attacker manages to obtain 50% of the stake of the PNK but the mechanisms to attribute SBTs are secure, then you can hope that the court will still be secure. If the attacker manages to break the SBT attribution mechanisms, she should still need a very large percentage of all PNK in order to mount a viable attack. In the previous blog article we saw that proof-of-personhood tools such as Proof-of-Humanity can be used in ways that give such complementary defenses.

Using one or many SBTs in juror drawing

The most straightforward way that SBTs could be use in juror selection would be to just impose a requirement that in order to be drawn in a specific court or in certain cases, a juror needs to possess a given SBT. In order to have any chance of being drawn in a juror in a court that handles cases related to smart contract bugs, one needs to have the Solidity developer SBT.

This drawing mechanism is fundamentally similar to drawing using proof-of-personhood tools such as Proof-of-Humanity. The mechanism essentially filters which jurors can be drawn – you either have the required SBT and are eligible or you do not. In particular, this setup has the same attack model as that of drawing mechanisms using proof-of-personhood, so you can check out our previous blog article for an analysis of its attack resistance.

If you have a community of jurors who have a variety of backgrounds, a more ambitious approach is to use their SBTs to try to draw jurors with complementary backgrounds. Here you essentially want to group jurors with similar SBTs.

Note that you will not necessarily have 1 SBT equal 1 group. Some SBTs could give you very similar information about the jurors. For example, users with SBTs attesting to their expertise in Solidity development may also be likely to have an SBT attesting to their expertise in Python development whereas the jurors who have an SBT attesting to their knowledge of insurance contracts may be a largely disjoint set of people.

By using a modern clustering algorithm such as spectral clustering we can sift through what information is redundant and what SBTs really deserve extra weight. We sketched this idea at the end of the previous blog article.

Note that these algorithms have been traditionally deployed in centralized settings where a central authority can limit the ability of hostile parties to manipulate the results. Thus we want to do a deep analysis of the attack resistance of this approach to make sure that it is appropriate for a decentralized environment.

Review of Spectral Clustering

We will follow spectral clustering as it is presented in A Tutorial on Spectral Clustering by Ulrike von Luxburg, adapting that presentation to our application of SBTs.

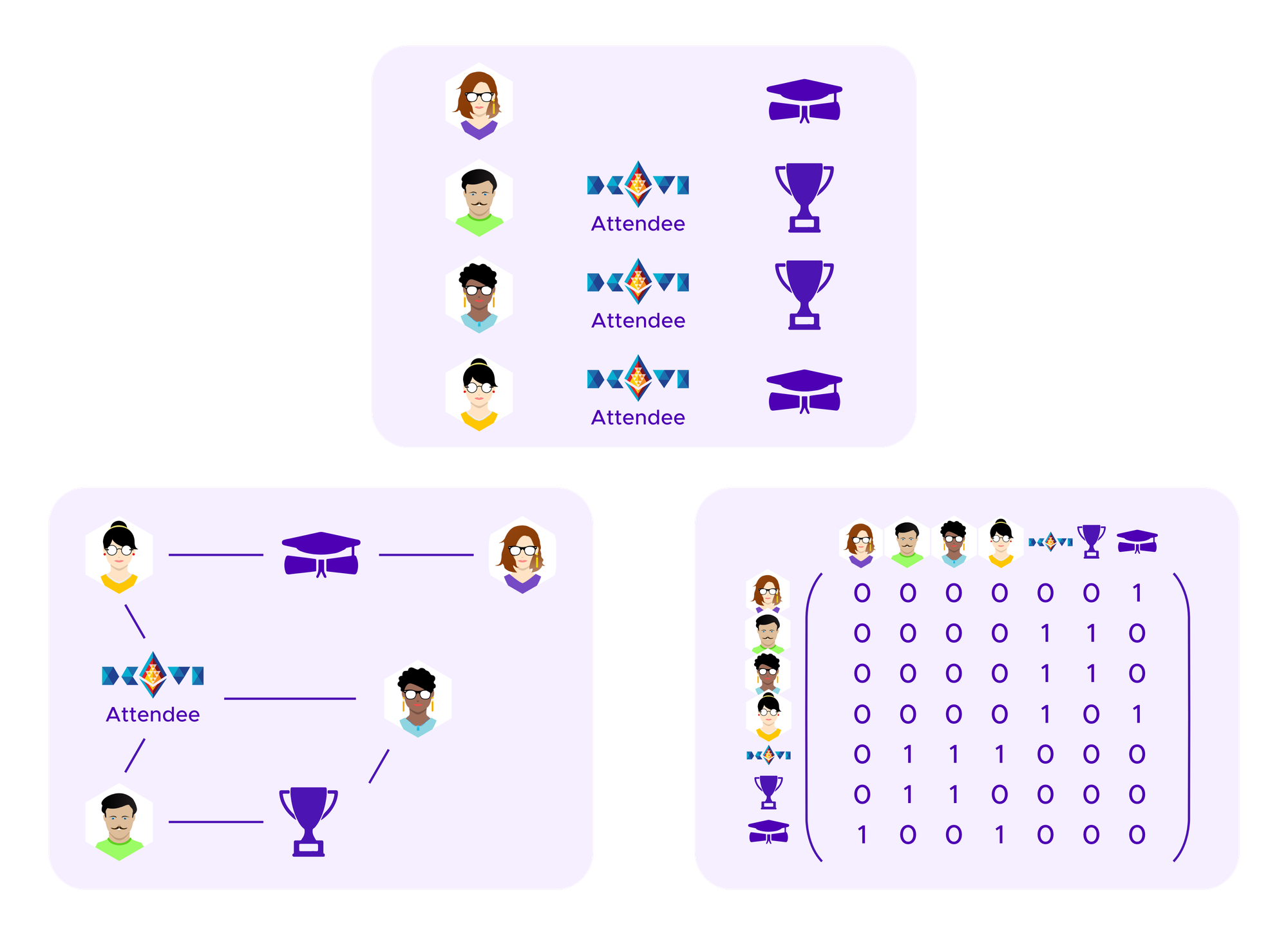
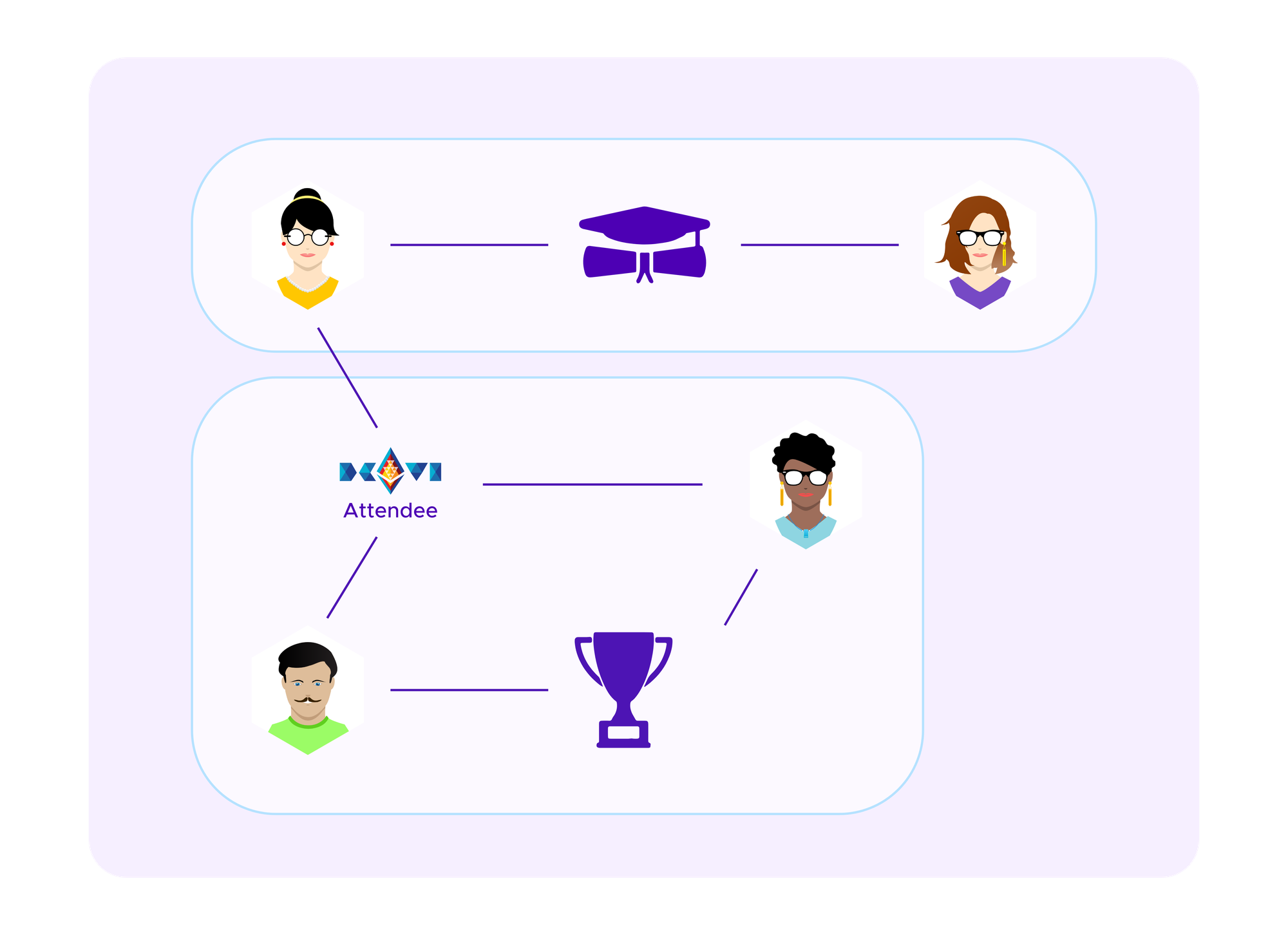
One starts by creating a graph that represents which users have connections to each other, in this case which users have which SBTs. This can then be encoded in a symmetric matrix where there is a 1 in entries corresponding to where a given user has a given SBT and 0 otherwise. Note that, in our application, this is a bipartite graph as edges only ever connect users and SBTs. One does not have edges between two users or between two SBTs.

We will consider various ways that the candidate clusters c1,...,ck, namely sets of vertices and edges in the graph, are recombined, so we introduce some notation. We write

to indicate the complement of cj. Namely, this set consists of all vertices and edges that are not in cj.

Similarly, we write

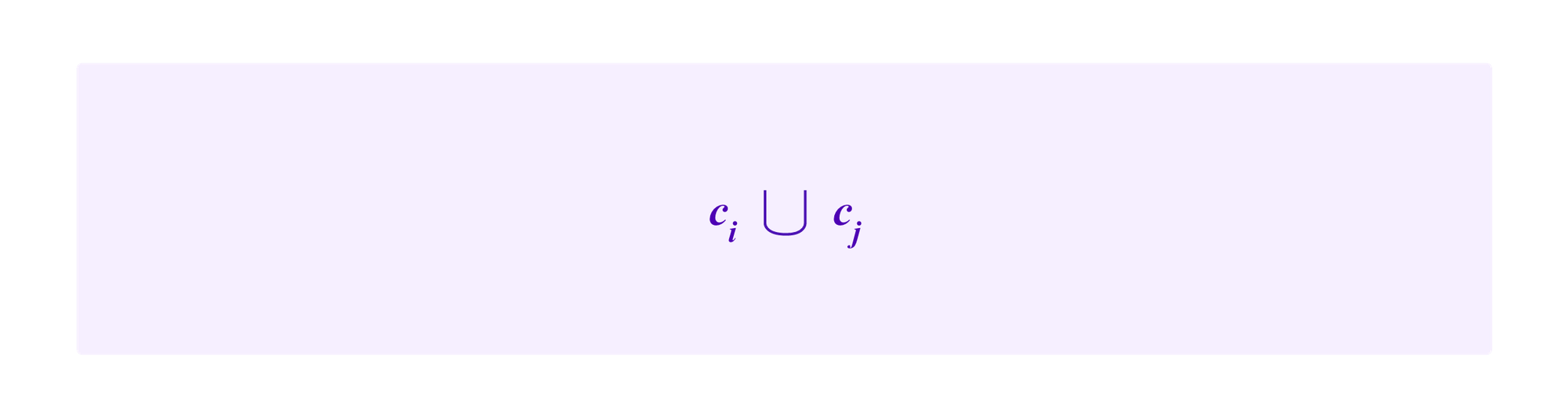
to indicate the union of ci and cj. This is the set of all vertices and edges that are either in ci or cj.

Then one intuitively wants to split the graph into clusters so that there are as few edges as possible that cross from one cluster to another. If one wants to produce k clusters, one might try to cut up the jurors and SBTs in candidate clusters c1, …, ck that minimize:

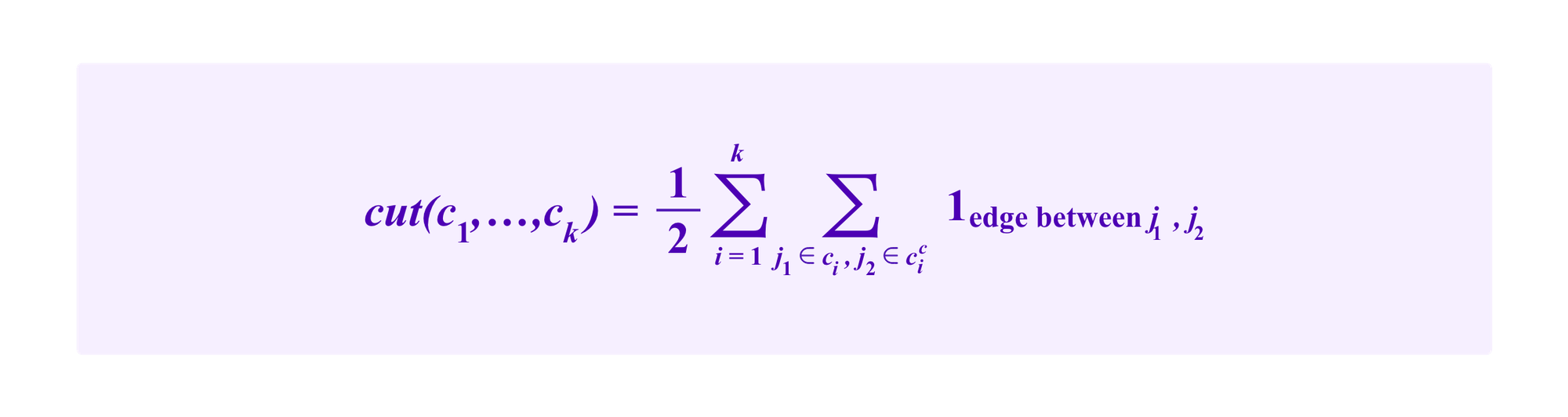
Here the

is an indicator function that is 1 whenever there is an edge between j1 and j2 (where j1 and j2 can be participants or SBTs) and 0 otherwise. One includes the ½ in this formula to account for the fact that any edge from j1 to j2 will also count in another term as an edge from j2 to j1.

Namely, minimizing cut(c1,...,ck) minimizes the total number of edges that pass from a cluster to its complement, that is to say to another cluster.

However, choosing clusters to minimize cut(c1,...,ck) in this way may produce clusters of very unequal size. Some clusters may wind up with only a few elements in them. Then one wants the clustering algorithm to penalize very small clusters, pushing towards choosing clusters of comparable size.

Two standard ways to do this that are presented in the tutorial. One chooses clusters c1,...,ck that minimize one of the two following formulas:

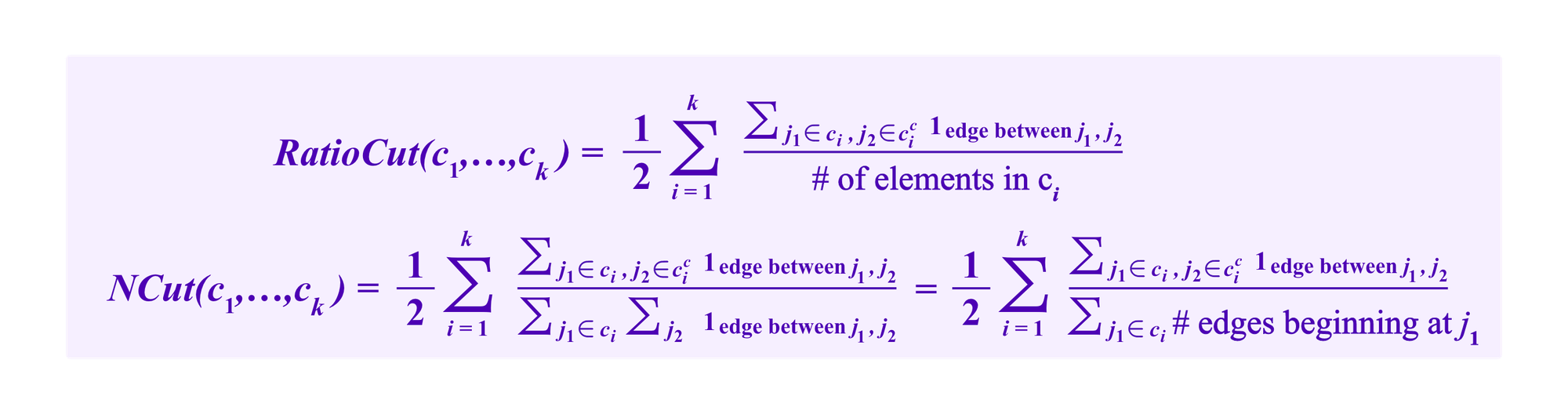
Here the terms in the denominator correspond to notions of size of the clusters, the number of elements in each cluster for RatioCut and the number of edges beginning in that cluster for NCut, so that the terms for a small cluster are made larger.

The discrete optimization problem that consists of actually computing the cluster assignments c1,...,ck that minimize these quantities is NP hard. However, it turns out that one can perform good approximations of these optimization problems using a matrix called the “graph Laplacian”.

The graph Laplacian is a matrix that is derived from the matrix above that encodes the information about who holds what SBT. One can show that its eigenvectors give information about the clusters of the graph.

If one considers a graph that perfectly breaks into k connected components, namely k regions that are each connected by paths of edges within themselves but for which there is no path of edges going from one component to another, then the graph Laplacian has 0 as an eigenvalue with multiplicity k and one can take corresponding eigenvectors that allow one to read off the elements that are in each component.

Then, it turns out that if the graph approximates breaking into clusters well, the eigenvectors corresponding to eigenvalues that are close to 0 still give useful information about how to cluster the graph.

Moreover, the problems of minimizing the RatioCut and NCut formulas above can be shown to be equivalent to discrete problems that when “relaxed” to allow continuous solutions can be solved by, once again, looking at the eigenvectors of the graph Laplacian – specifically, there are different versions of the graph Laplacian depending on how or if one “normalizes” them and performing spectral clustering with one version corresponds to approximating minimizing RatioCut while using another version corresponds to approximating minimizing NCut.

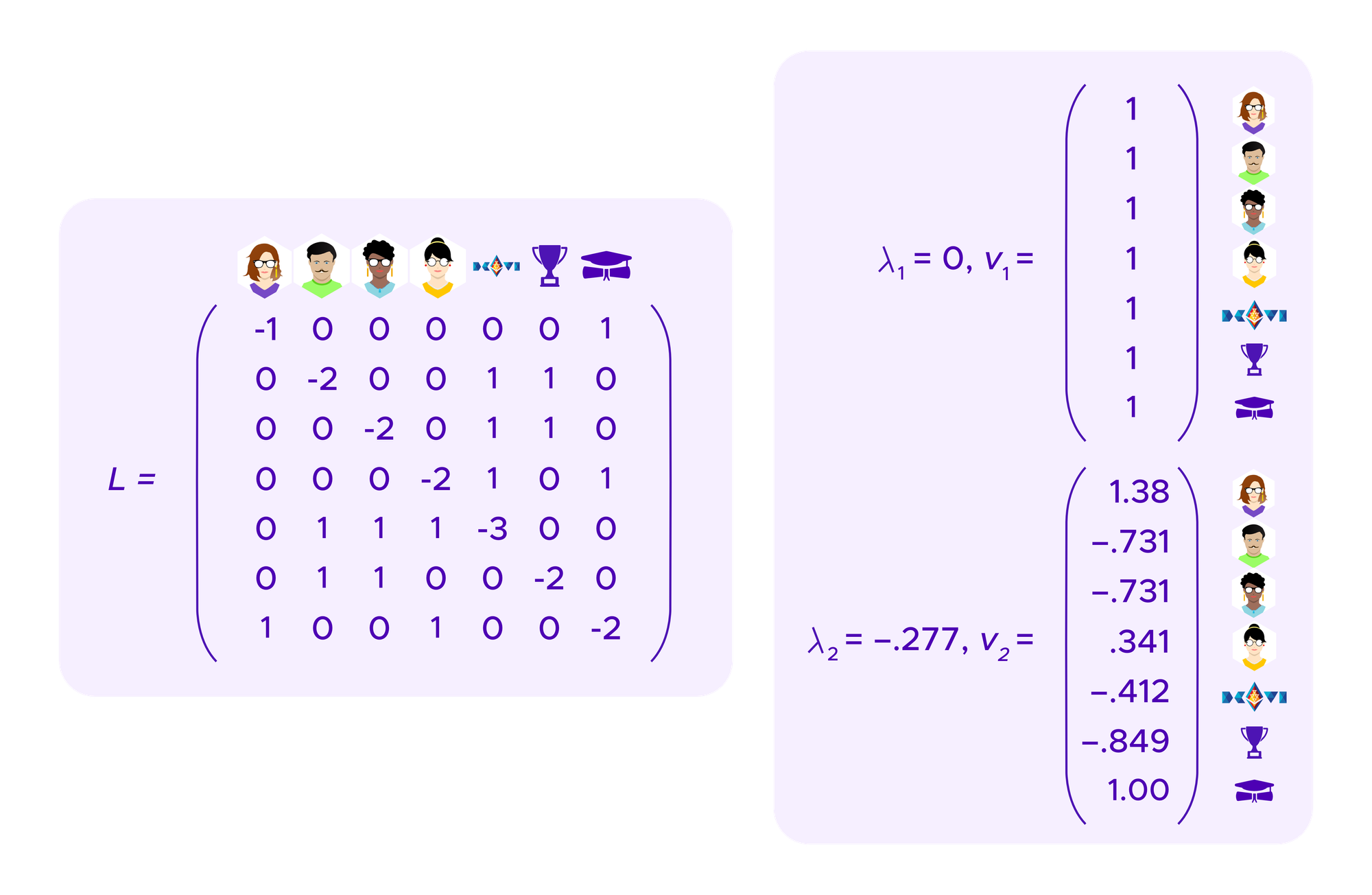
Below we will look at how the choice of using RatioCut versus NCut impacts attack resistance properties when one uses spectral clustering of SBT information in Kleros.

Mechanisms that one can weight with SBTs

Recall that in our previous article we looked at two blockchain-based mechanisms with which it might make sense to use SBT-weighting: quadratic funding and Kleros juror selection. We will continue to mostly study these two applications, so we briefly review both their classic, “unweighted” versions and how SBT-weighted versions of them using spectral clustering might look.

Quadratic funding

Quadratic funding is a mechanism to allocate subsidies, for example, to public goods. Each participant j contributes xj. Then the public good receives

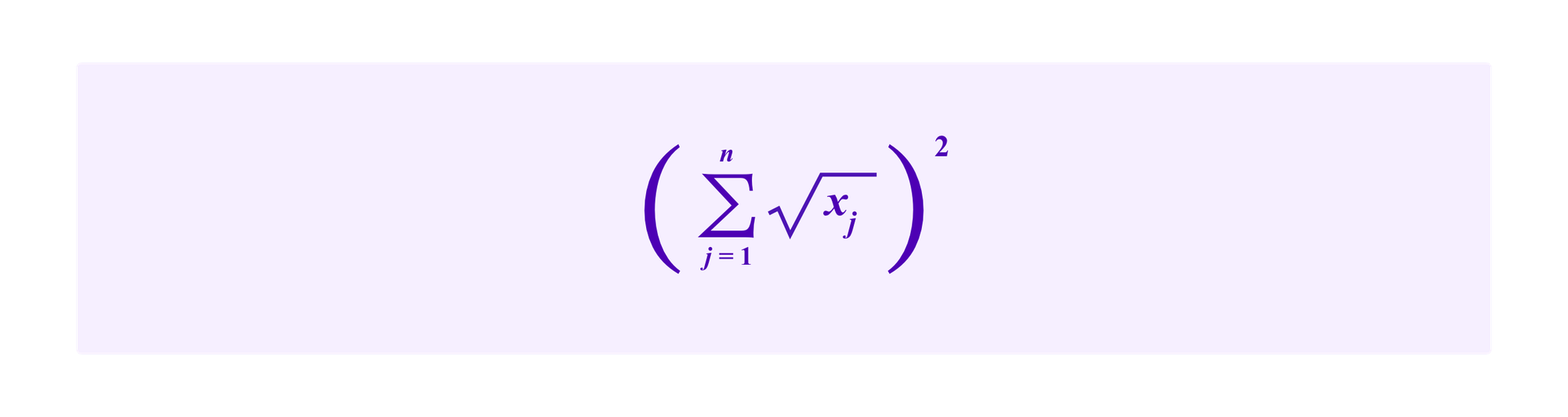
So, deducting the contributions themselves, this means that the project received a subsidy of

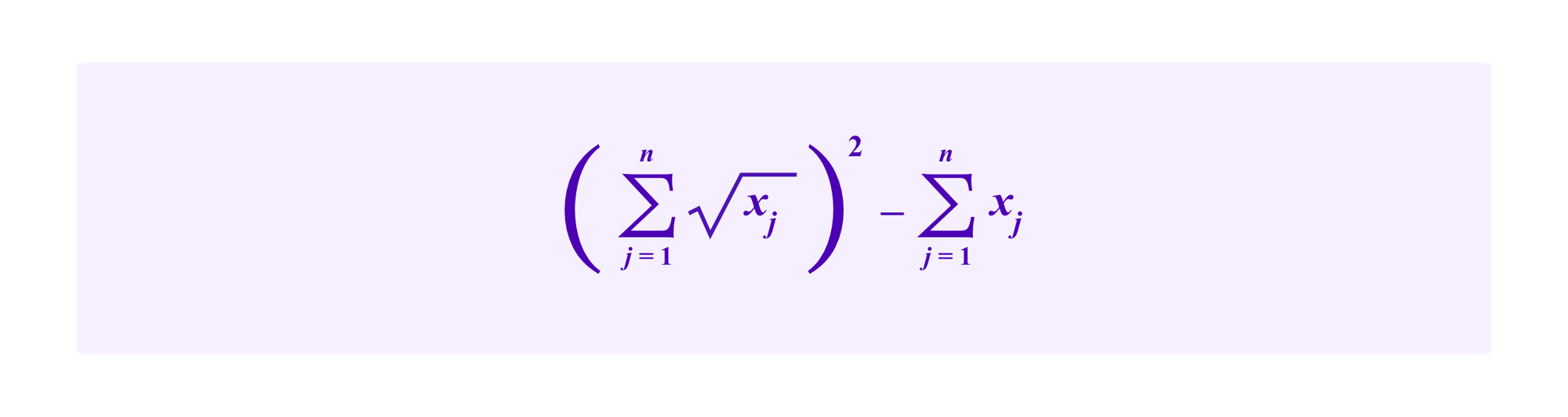
The idea here is that a wealthy individual that makes a very large subsidy will generate less and less matching funds from the subsidy mechanism for each extra dollar she puts in. For a given amount of total contributions to a project, the project receives more subsidies if the contributions come from many participants who each make a small contribution.

Then, a refinement of this idea discussed by Miller, Weyl, and Erichsen considers putting the contributions of all participants in a cluster together under the square root. Now projects receive a total amount of:

This has the result that projects should get contributions from participants in lots of different clusters in order to have large subsidies. If the clusters accurately reflect meaningful social information about the community, this would mean that the project has support from many people with diverse backgrounds.

Kleros juror drawing

Our main motivation with this research is to include similar social information into Kleros juror drawing. In Kleros 1.0, each time a user is drawn to resolve a dispute, a given user i has a chance of being drawn that is proportional to her percentage of the total stake in the relevant court. Namely, if each user j stakes xj, then i's chance of being drawn is given by:

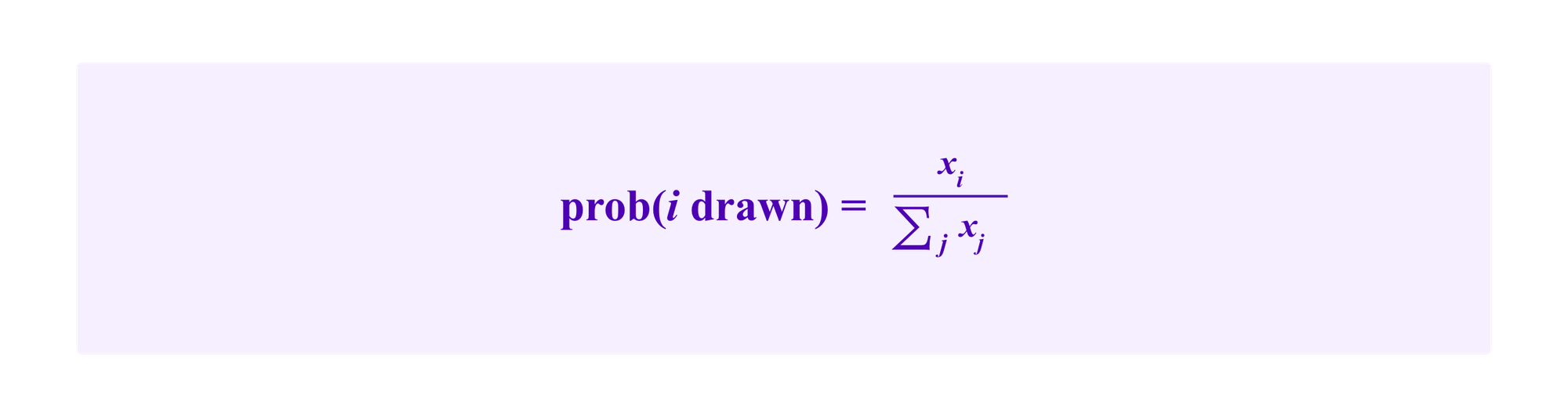
Then, if SBTs are used to partition the users into groups, we argued in the previous article that a formula analogous to the one above for quadratic funding would give the user i who is partitioned into group c* a chance of being drawn of:

Then, the fundamental question is how does one go about partitioning users into groups for this process. We are particularly interested in how robust this process is against potential attacks.

Attacks that change what clusters are chosen

In this analysis we will consider a pessimistic attack model where the attacker has broad powers to manipulate the social information that we want to make use of.

Attack model:

• We assume that an attacker is capable of generating multiple profiles with which she might have SBTs. In particular, if a proof-of-personhood mechanism like Proof-of-Humanity is being used, we assume that the attacker is capable of bypassing it to obtain extra profiles.
• Furthermore, we assume the attacker is capable of attributing fake SBTs to her own profiles as well as potentially attributing fake SBTs to the profiles of honest users.

Nonetheless, we typically think of there being an economic cost to the attacker for performing these types of manipulations. If an SBT is issued by some institution, the attacker might have to perform a bribe to corrupt an insider at that institution to issue her malicious SBTs.

If an SBT is obtained by a curated list secured by Kleros, the attacker might take the strategy of recruiting people who actually deserve the SBT to fraudulently submit their credentials on her behalf. Thus, the attacker would have to pay an amount for each SBT maliciously obtained in this way.

Note that, in our attack model, attackers are assumed to be able to break proof-of-personhood mechanisms like Proof-of-Humanity. Indeed, having Sybil profiles is often a prerequisite of any attack on SBT-weighted mechanisms.

If the attacker can only control one profile, and hence one vertex in the social graph of users and SBTs, she will generally not be able to get an entire cluster to herself and will just represent one profile among many in whatever cluster she winds up in. Unless the clustering algorithm we use is very sensitive to small changes, arbitrary changes to a single vertex should not result in a large change in the outcome.

We will consider a heuristic where we calculate the scores of just two possible sets of clusters under these formulas: the cluster where all vertices are in the same clusters as one has in the absence of attackers, c1,...,ck, or a clustering where two of these clusters are combined ci and cj and there is an additional ca given by profiles of the attacker that all share a single SBT and have no other edges.

It will typically be the goal of the attacker to have ca recognized as a separate cluster, making her profiles seen by the algorithm as a group with a distinct viewpoint that needs to receive extra weight.

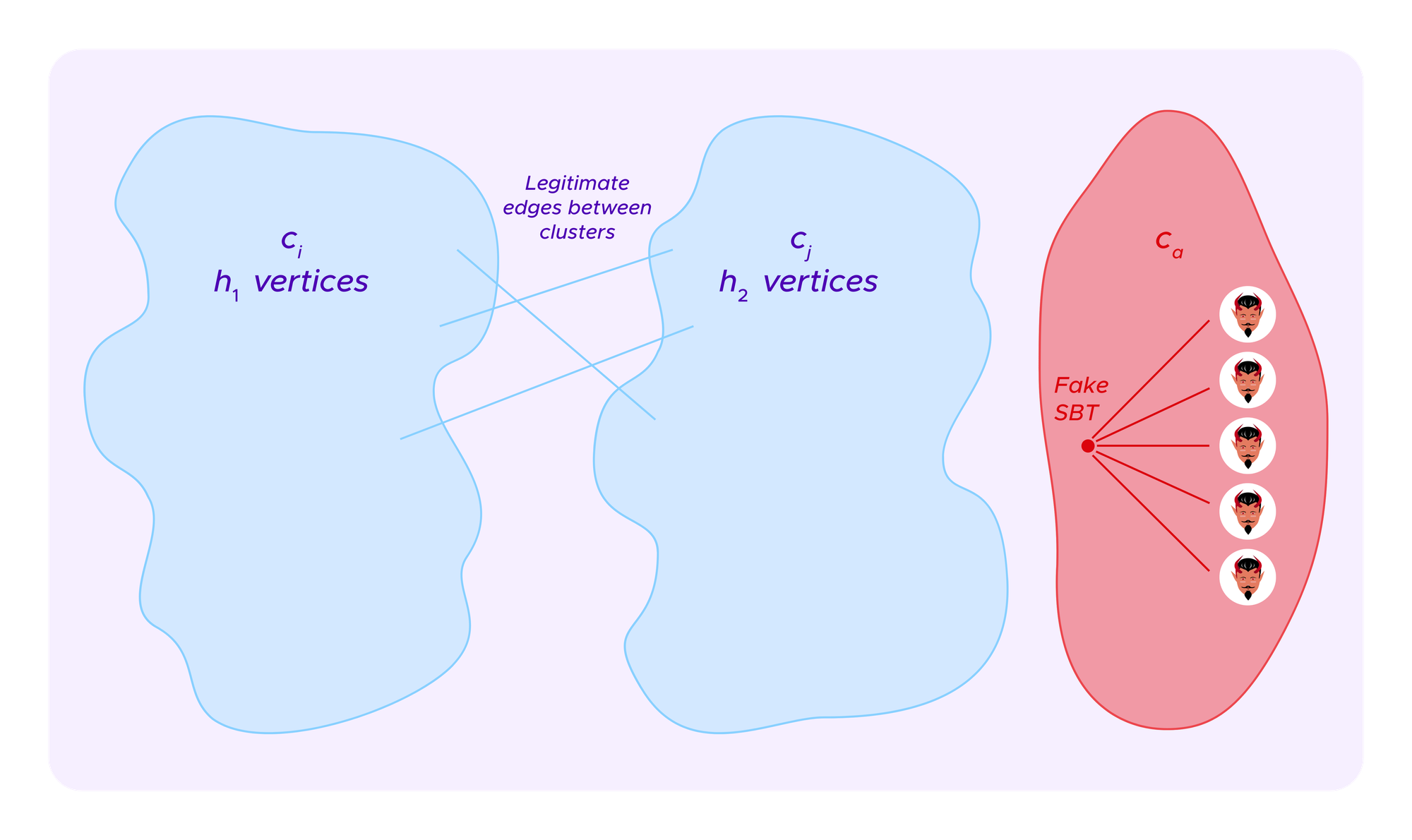
We keep track of the various quantities that will be relevant as we look at these pieces of the graph. We suppose cluster ci has h1 vertices and the number of edges that start in ci but leave it towards some cluster other than cj is given by:

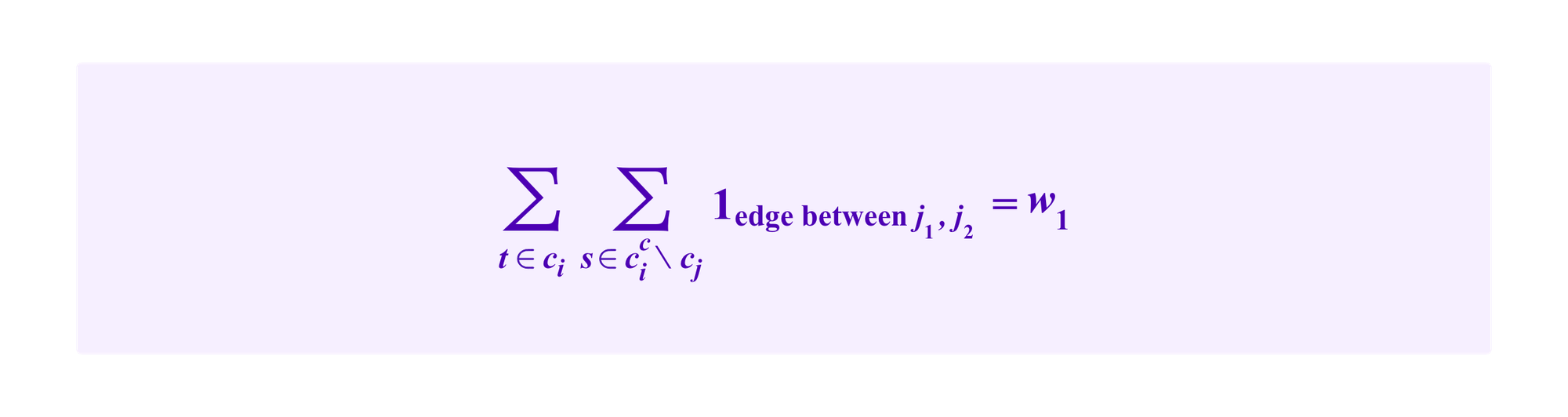
Similarly counting the edges that go from some t in ci to some other point s in ci (counting double as each such edge also counts as an edge from s to t) we have:

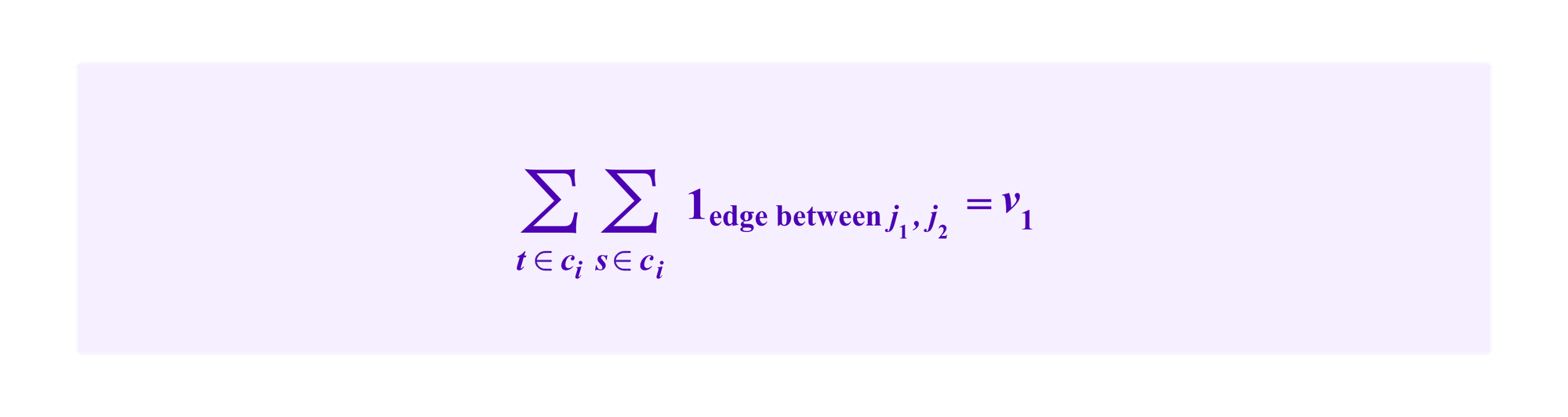
Similarly, cj has h2 vertices and

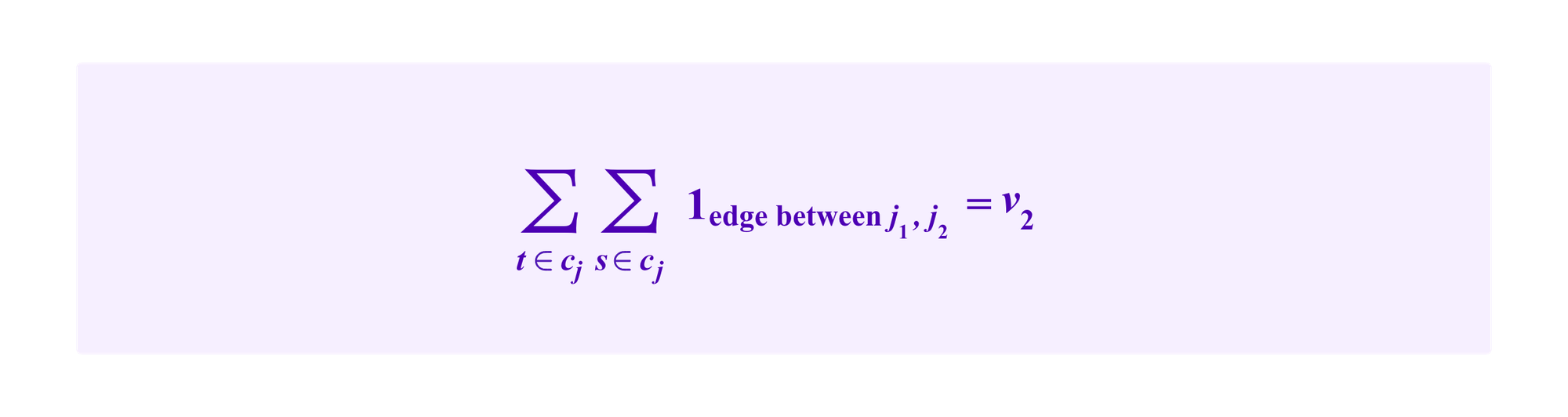
and

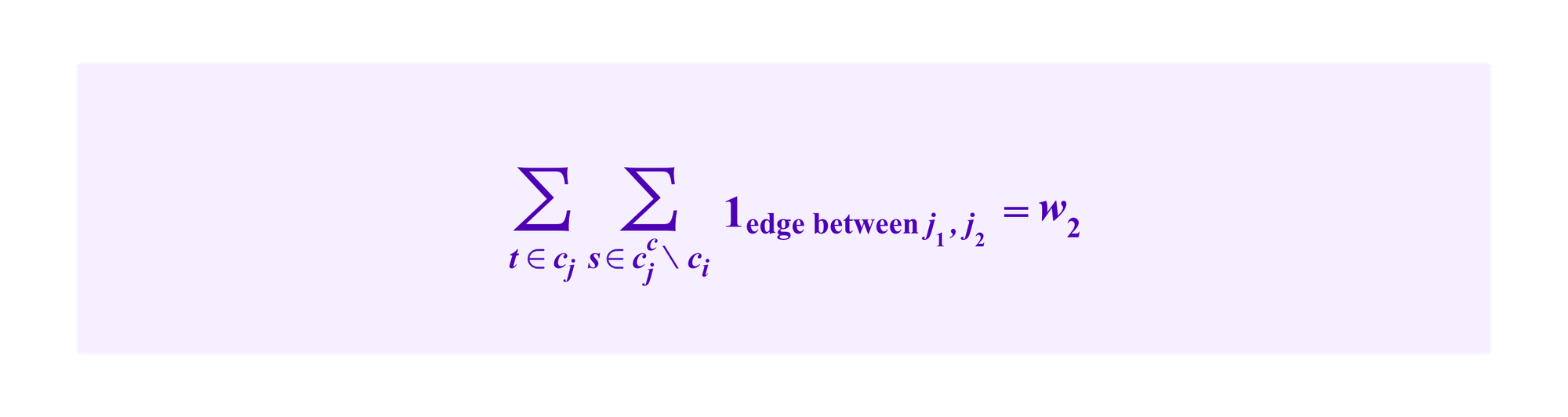
Finally, we count the number of the edges between ci and cj as

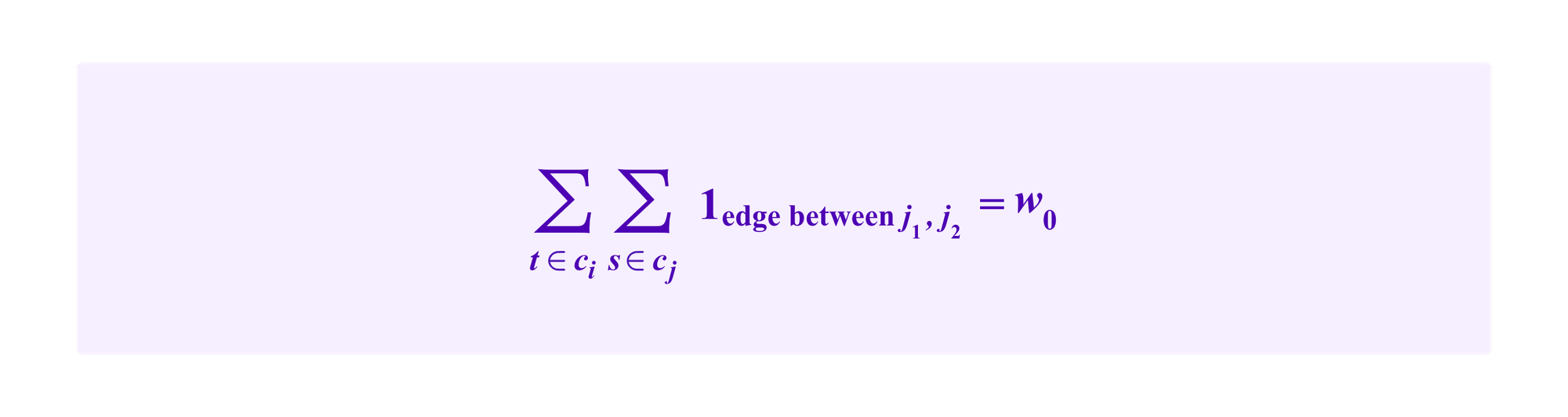
Suppose the attacker has already attributed herself a-1 profiles with a given fake SBT that form the alternate candidate cluster ca consisting of a vertices.

We will analyze the effects of various attacks on spectral clustering. For some of this analysis, it will be easier to work with the exact formulas for RatioCut and NCut than analyzing these attacks on the spectral clustering algorithms directly.

Of course, the RatioCut and NCut formulas give the exact, discrete optimization problem that one would want to analyze in an ideal world for which spectral clustering only gives us approximate optima. This will conversely mean that our analysis on the RatioCut and NCut formulas will only give us approximations of what will happen when an adversary launches these attacks against the spectral clustering algorithms. As the spectral clustering algorithms are what we are actually capable of implementing in applications like quadratic funding or Kleros, it is these algorithms that we want to be attack resistant.

Each cluster corresponds to one term in the formulas for RatioCut or NCut. So we consider the two terms in these formulas for each of the possible clusterings we consider: either ci will form one cluster with cj and ca combined to form the other, or ci and cj will be combined into one cluster and ca will be the other.

An immediate problem for taking this approach in an attack resistant way is that

So, then

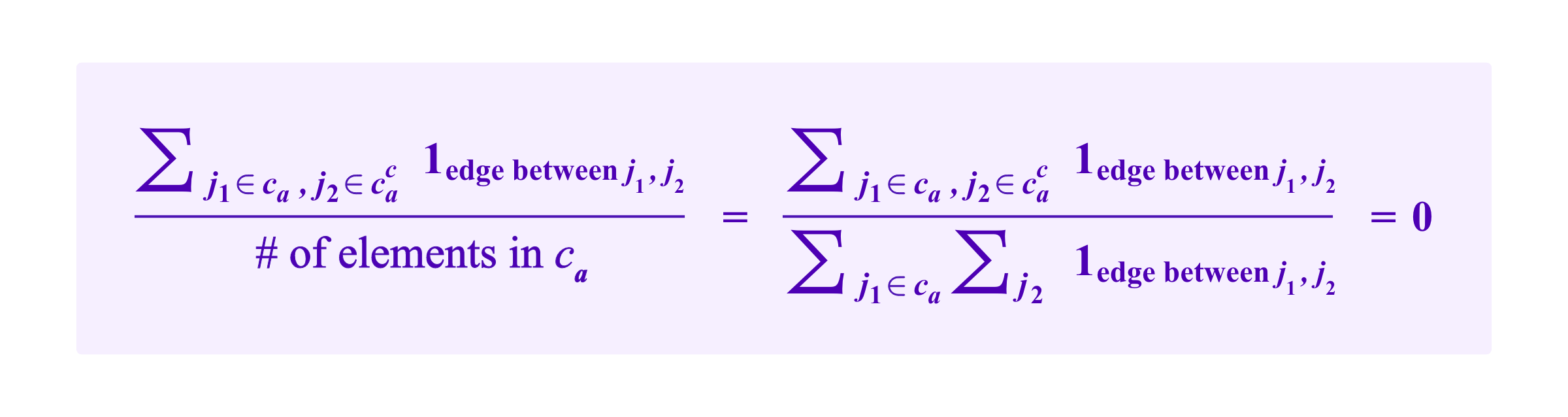
Namely, the term corresponding to ca in both RatioCut and NCut is 0, regardless of how many elements or internal edges there are in ca. Even though the RatioCut and NCut are designed to penalize taking very small clusters, these penalties drop out when the number of edges connecting ca to the rest of the graph is actually zero.

Then, by placing a fake SBT and Sybil profiles that take the form of ca, the attacker can always manipulate the algorithm so that ca is always taken as its own cluster before ci and cj are taken to be separate. Indeed, we calculate

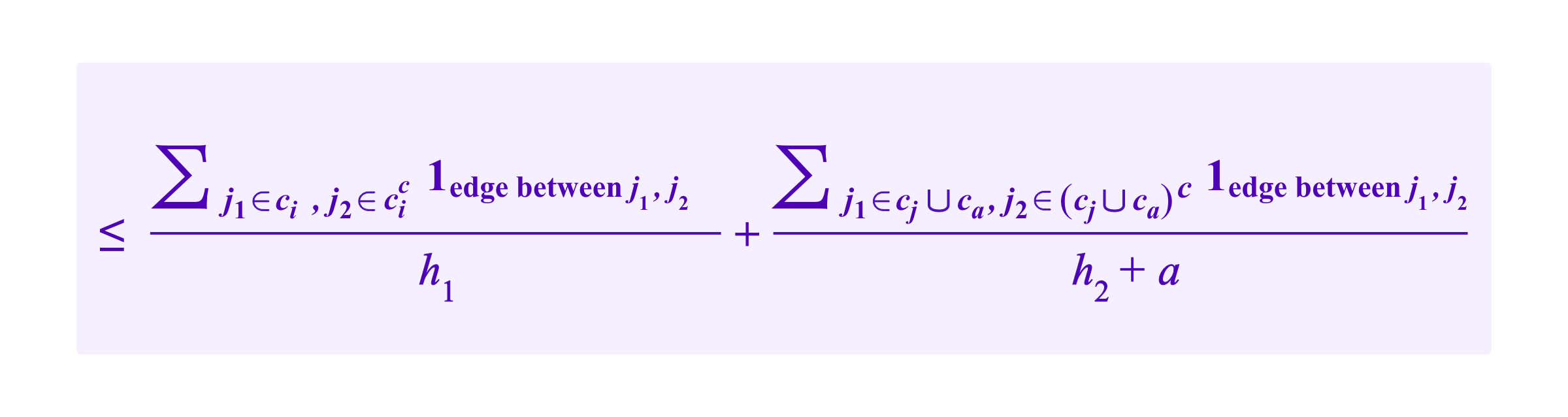
where the second to last line holds as long as a<= h1, which the attacker can arrange her Sybil identities to achieve. So, the two terms from taking clusters ci and cj combined and ca separate contribute less to RatioCut than taking clusters ci separate and cj and ca combined.

One can perform a similar computation for NCut. Initially, this might seem to make spectral clustering approachs, at least ones based on RatioCut and NCut, unviable. However, it is possible to modify our approach slightly to salvage these spectral clustering ideas.

We will add a point to the graph that is a common neighbor to all the other points, namely, a point that has an edge to every user profile and every SBT. Note that by doing this the graph is no longer bipartite. In some sense, this new point might be thought of as marking the belonging of all of the users and SBTs to a common ecosystem.

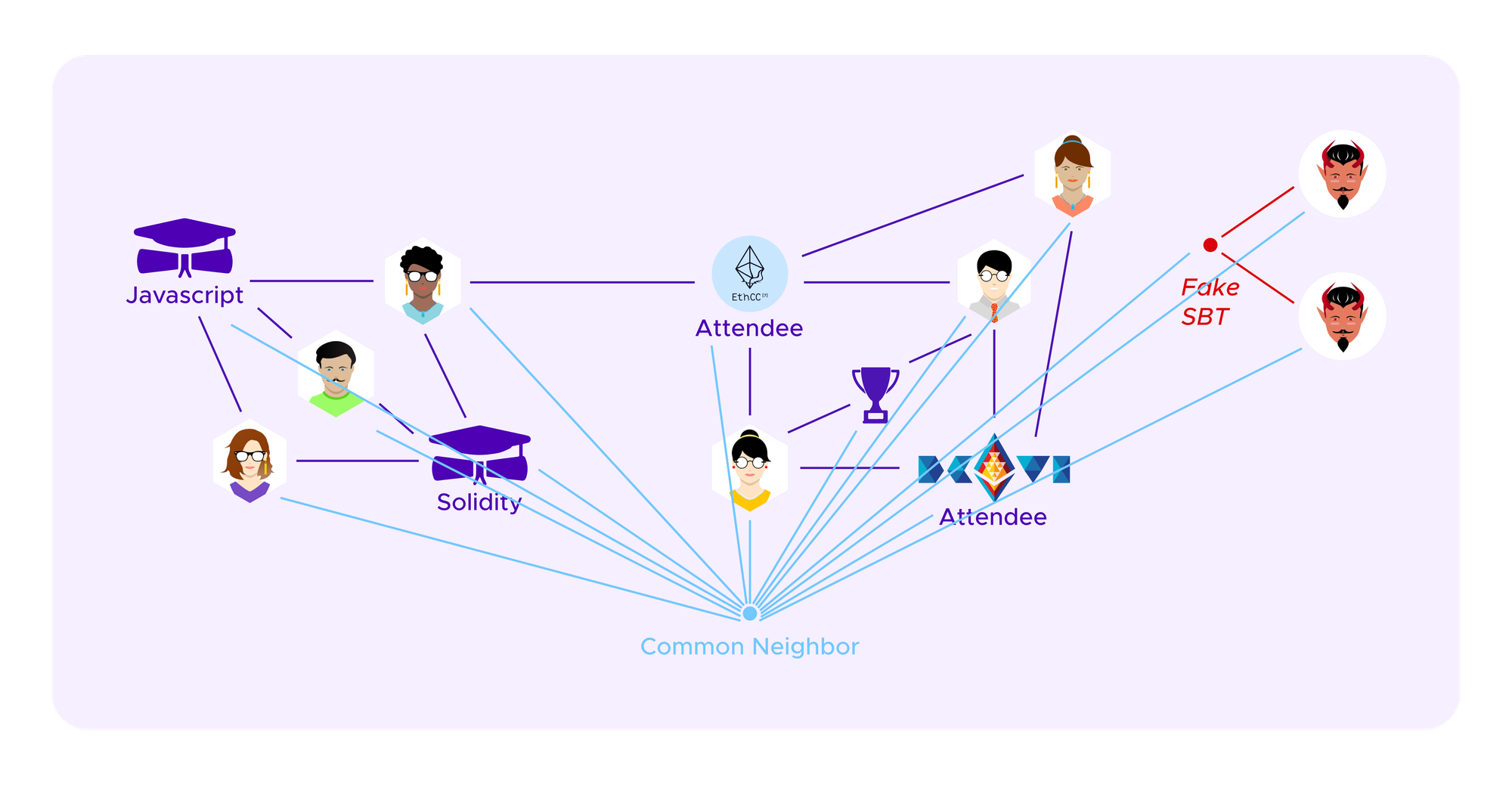
The idea here is that by giving ca a weak connection to the rest of the graph, the ca term in the RatioCut and NCut formulas will not just drop out so the effects of dividing by a small denominator penalizing ca as a small cluster will come through.

Heuristically, we suppose that the common neighbor winds up in some other cluster than ci, cj, or ca so that we don't have to account for its role in its own cluster. Then, with the notation above, this gives us a formula for NCut of:

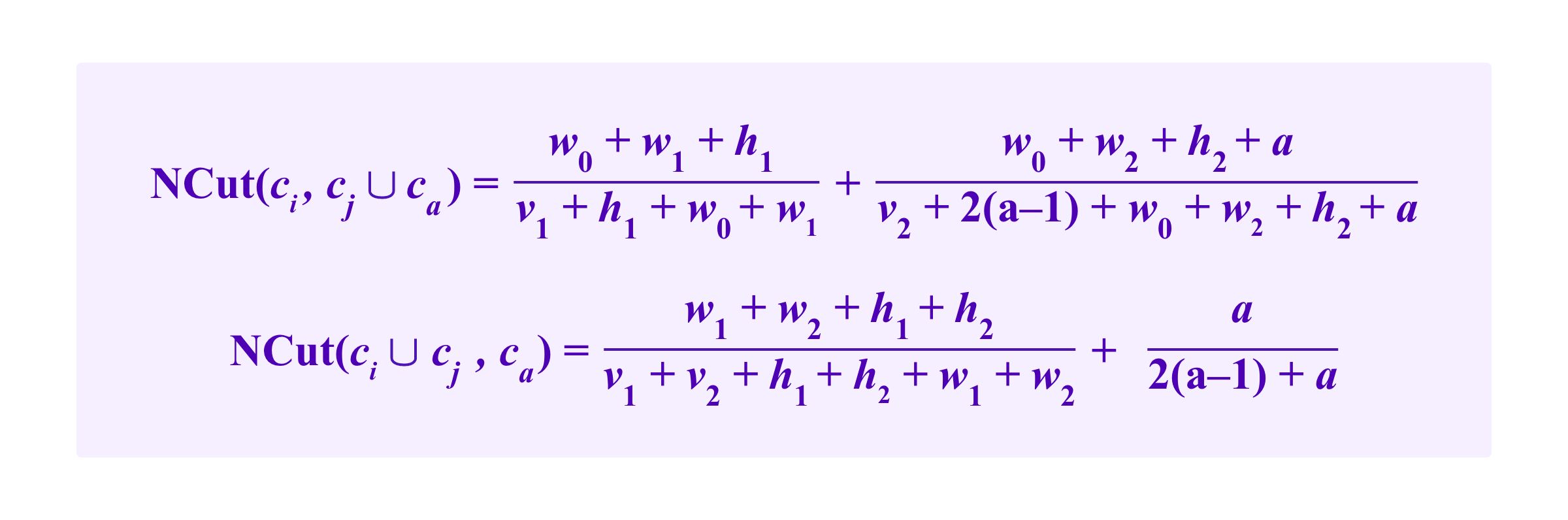
As one can see analyzing this formula and the example above, adding the common neighbor had the desired effect for NCut.

However, this idea does not work for RatioCut. Indeed, one can see the common neighbor causes one to add a number of edges of each cluster to the numerator of the term for that cluster that is equal to the number of points in that cluster. However, for RatioCut, this is also equal to the denominator of that term, so one is just adding one to each term with no net effect.

Two attack strategies to cause ca to separate

Now we will consider two basic approaches that an attacker might take to alter the clustering assignments:

• Internal attack - The attacker can attribute a fake SBT to honest participants. The idea here is that this will make honest profiles, which are normally not grouped together as they do not share significant similarities, seem more similar so that the a collection of the attacker's profiles seems more divergent by comparison and is more likely to be selected as a separate cluster by the algorithm.
• External attack - The attacker can attribute a fake SBT to her Sybil profiles. The idea here is that this collection of Sybil profiles, which seem similar as they all have the fake SBT, can break off and form a new cluster.
  

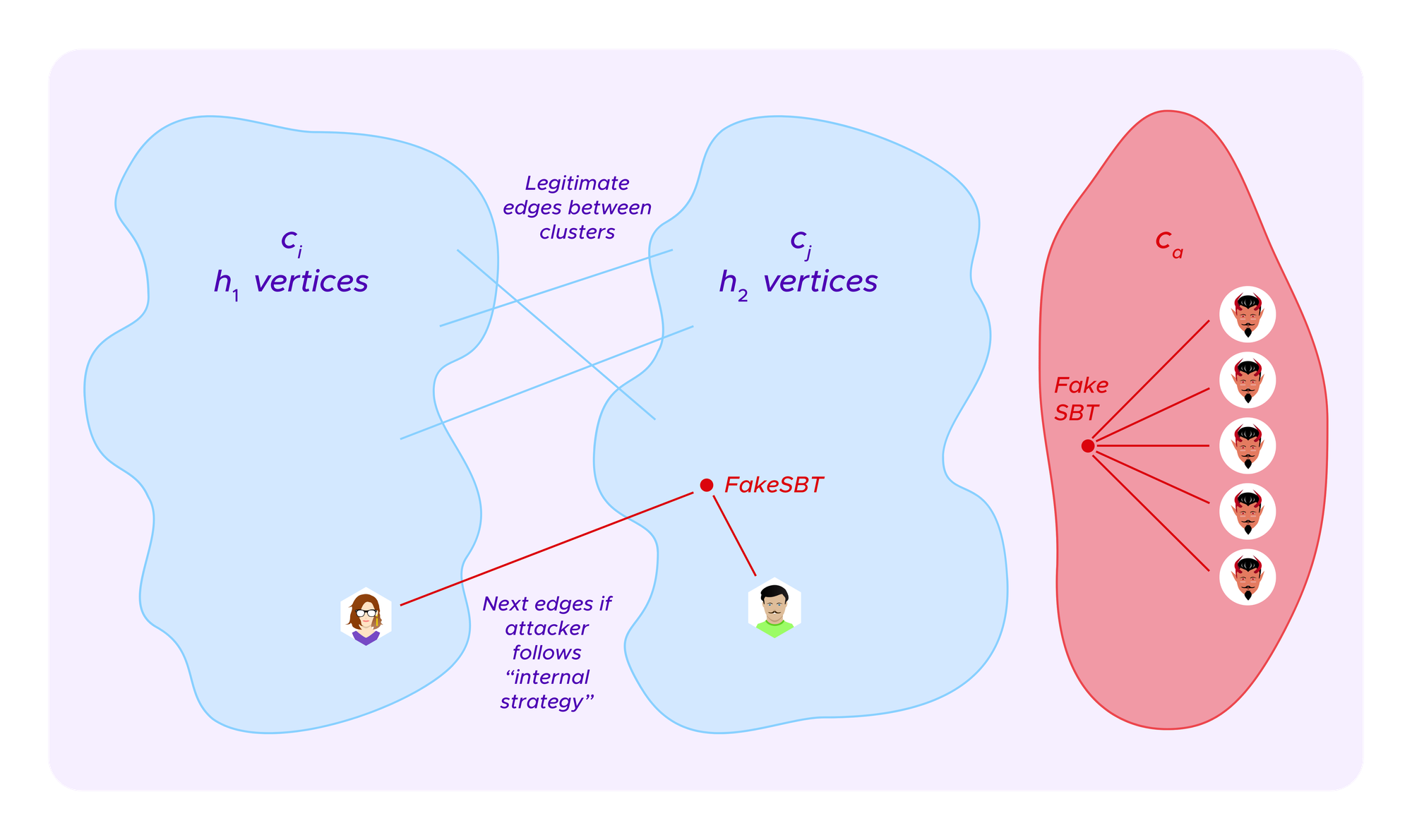
NB : As we have noted above, edges only ever go from a user to an SBT, and not between two users or between two SBTs. It is clear enough how an attacker can execute the external attack by adding a single edge between her profile and some malicious SBT. For the attacker to execute the internal attack, she cannot directly connect a user u1 in cluster ci to a user u2 in cluster cj. So, the first time she makes a malicious connection between these clusters she needs to place a malicious SBT and two edges, one to the user in each cluster.

Moreover, if the attacker places many more edges between u1 and the SBT than she places between u2 and the SBT, then the clustering algorithm will tend to assign the SBT to ci. Then, subsequent edges placed between u1 and the SBT do not increase the weight between the two clusters ci and cj.

Instead, if the attacker wants to increase the weight of the edges that go between ci and cj, with the ultimate goal of this causing the two clusters to collapse into one, she needs to place edges between u1 and the SBT in roughly equal numbers to edges between u2 and the SBT.

So then, allowing for the possibility that the attacker has already added some number of edges following either the internal attack and/or the external attack, we see the marginal effect of add two more edges following one or other strategy on the counters (w0,w1,w2,h1,h2,v1,v2,a):

Internal attack – add an edge from u1 to SBT and an edge from SBT to u2. Then we have

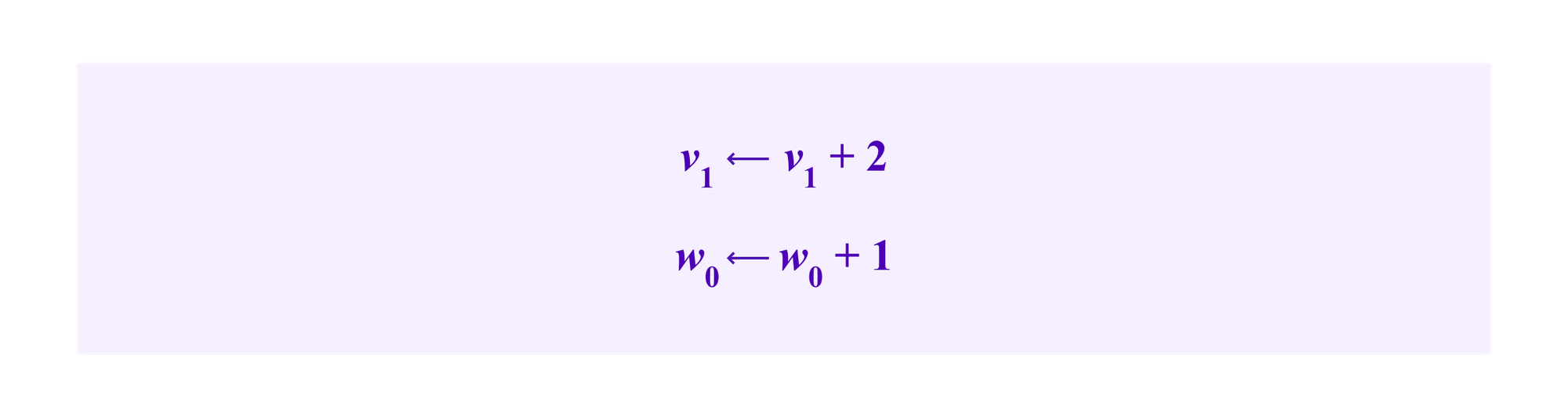
as the edge from u1 to SBT is counted twice in the count of the edges from one vertex in ci to another and the edge from u2 to SBT increases the number of edges between ci and cj by one.

External attack – add two edges from the fake SBT in ca to new Sybil profiles of the attacker which has the effect of

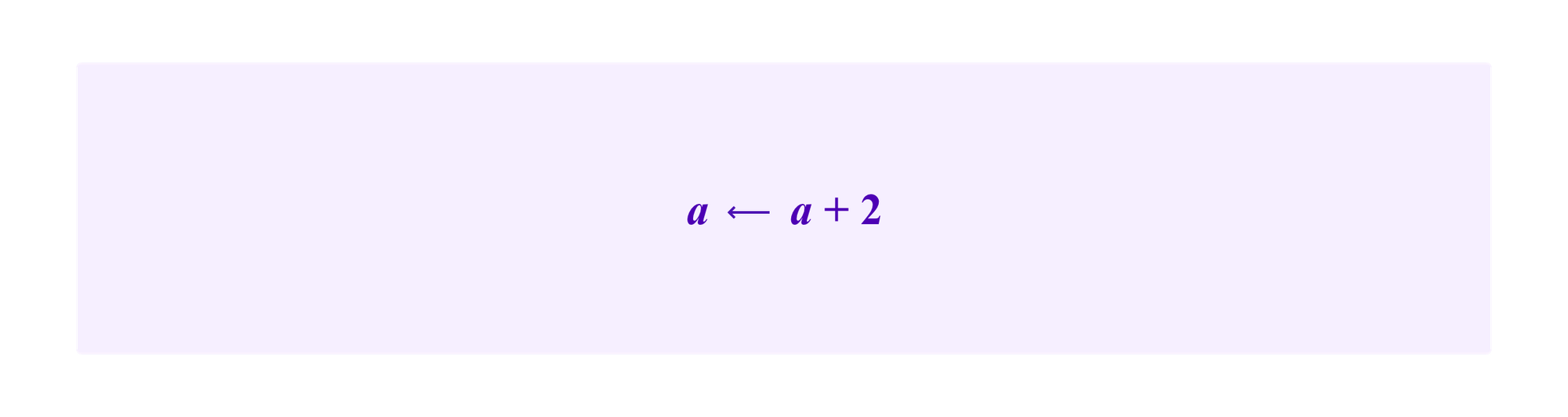
When making these substitutions in the formulas for NCut, we have that

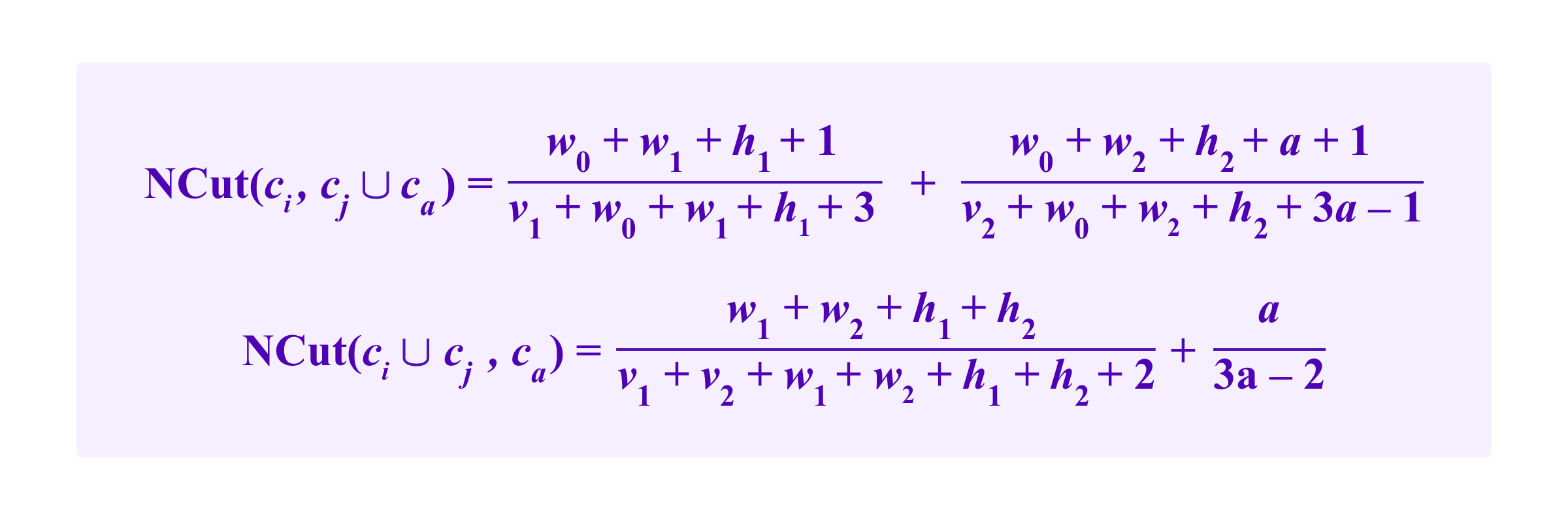
after the attacker adding two edges following the internal attack strategy and

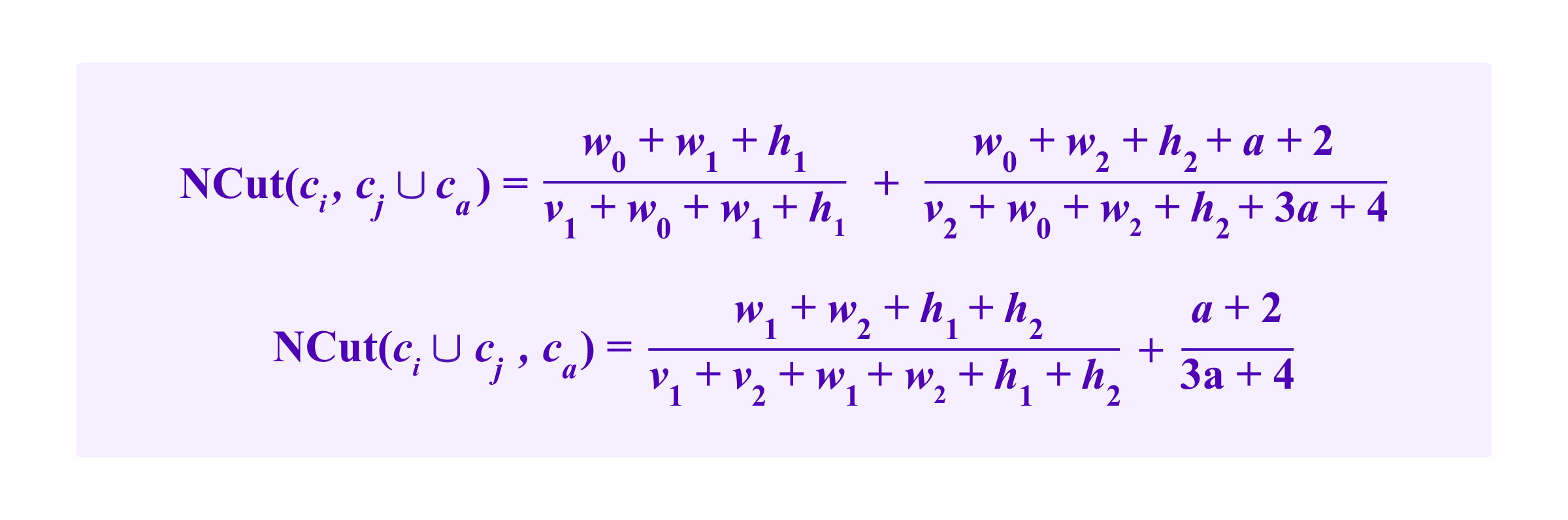
after the attacker adding two edges following the external attack strategy.

Then, to get a sense of in what conditions the attacker might pursue either the internal or the external attack, we can define

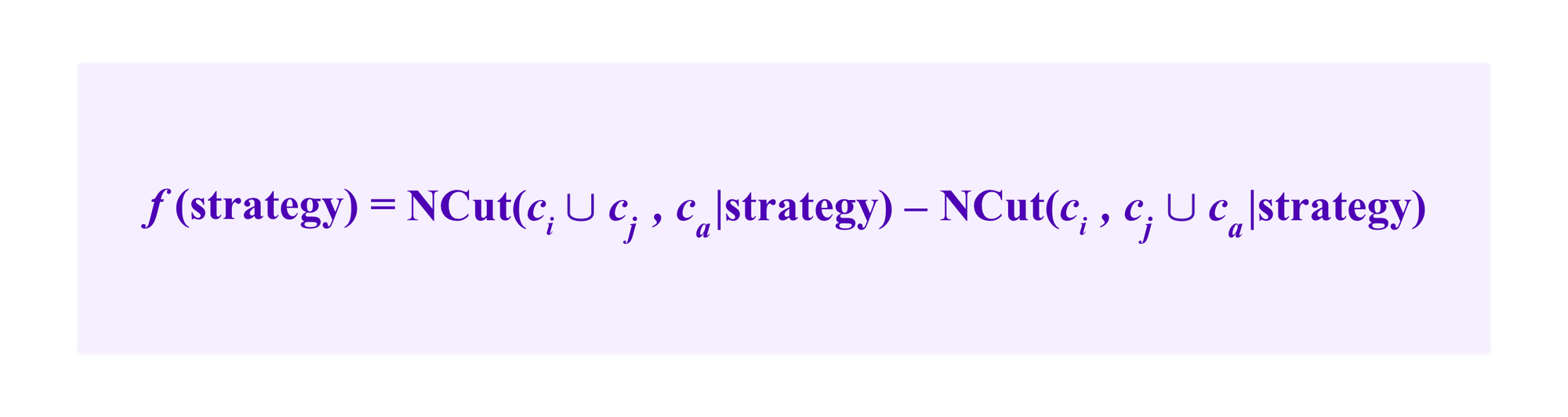
where strategy can be either spending the next two malicious edges placed by the attacker to perform the internal attack or alternatively using them to performan the external attack.

Then, as the clustering algorithm selects the clusters that minimize the NCut formula, one or the other of the attack strategies is effective in pushing towards the algorithm putting ci and cj together so that ca is separated out as its own cluster to the degree that the strategy can make

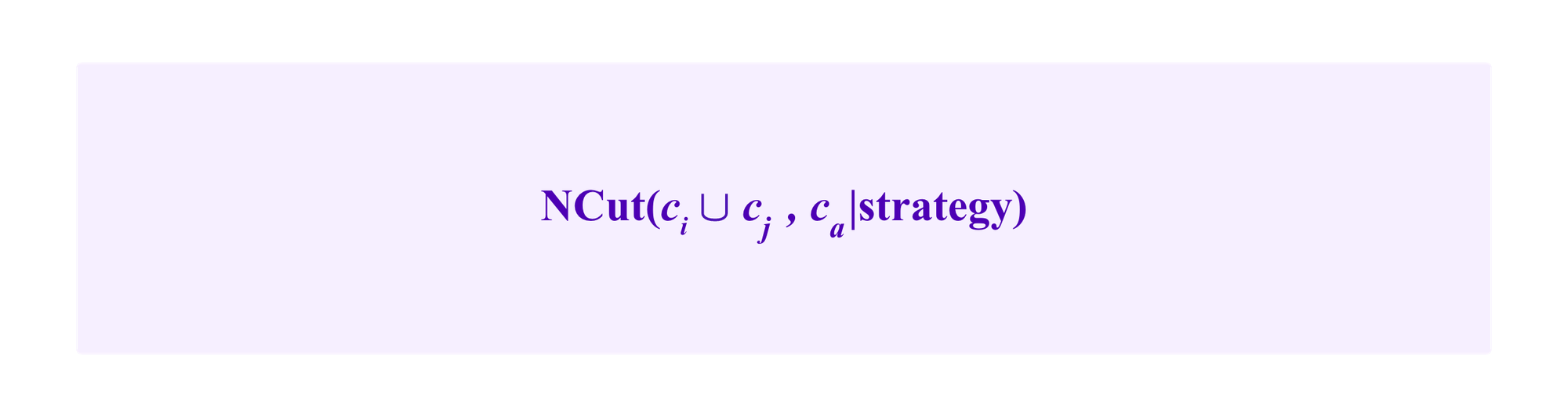
small relative to

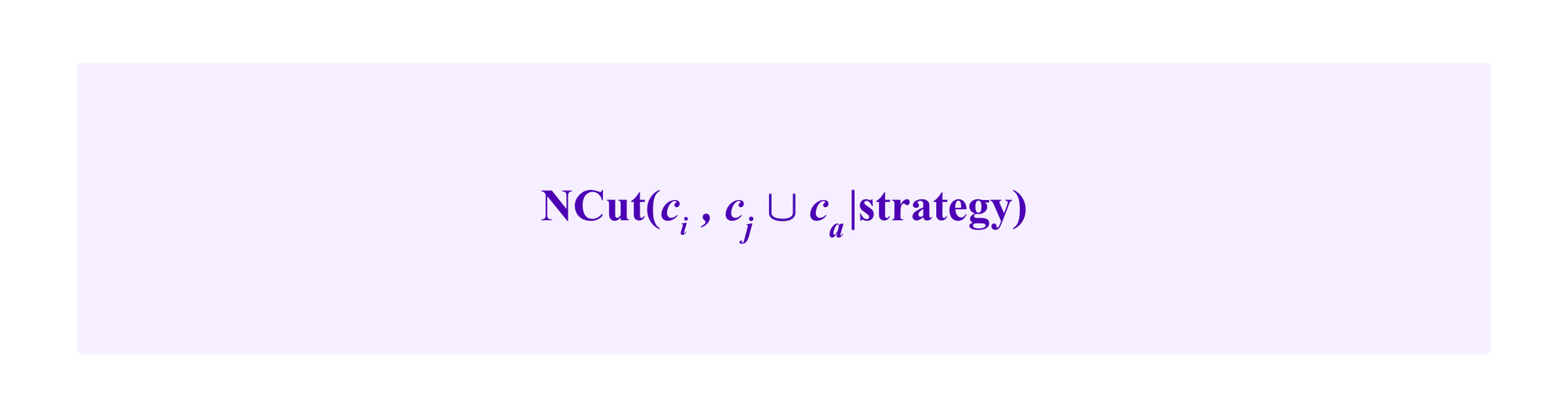
Namely, to the degree that f(strategy) is small.

Then, the attacker spending her marginal resources to pursue the internal strategy is more effective than her spending those resources to pursue the external strategy if

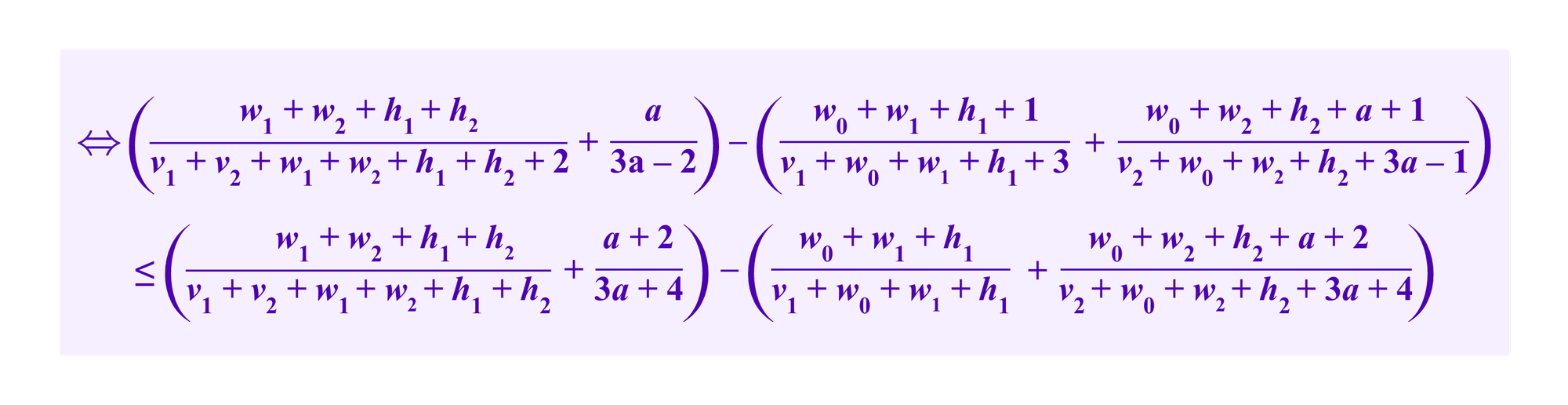
We make a few approximations to simplify this: we suppose that the clusters ci and cj are of roughly equal size so we take:

h1=h2

v1=v2

w1=w2

Also we suppose that the number of edges between ci and cj is typical of the number of edges between any two other clusters, so each of w1=w2 should correspond to roughly to the w0 edges connecting ci and cj respectively to each of k-1 other clusters. Namely, we take

w1=w2=w0*(k-1)

where k is the total number of clusters produced by the clustering algorithm.

Furthermore, we think of the number of user profiles being clustered and hence h1=h2 as being large relative to the constants that are in the denominators of some of the terms, so we drop those constants in any denominator that includes at least one of h1 or h2.

(v1, v2, w0, w1, w2, and a may or may not also be large enough that any constants in the denominators with them are more or less negligible. One would generally expect v1 and v2 to be somewhat greater than h1 and h2 if many users in ci and cj respectively share the same SBTs.)

Then, we heurestically/approximately have that

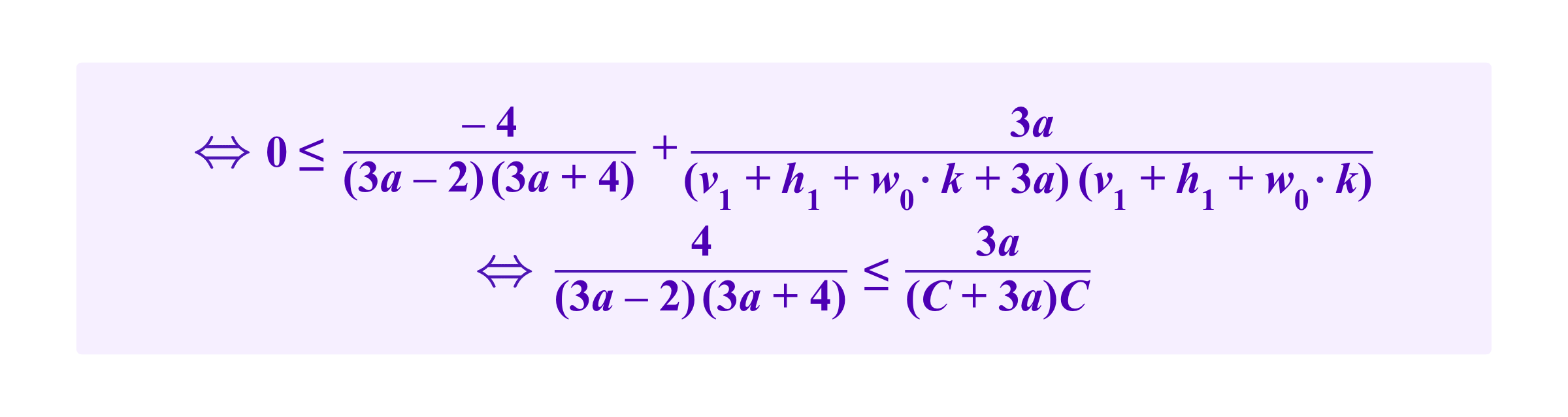
where

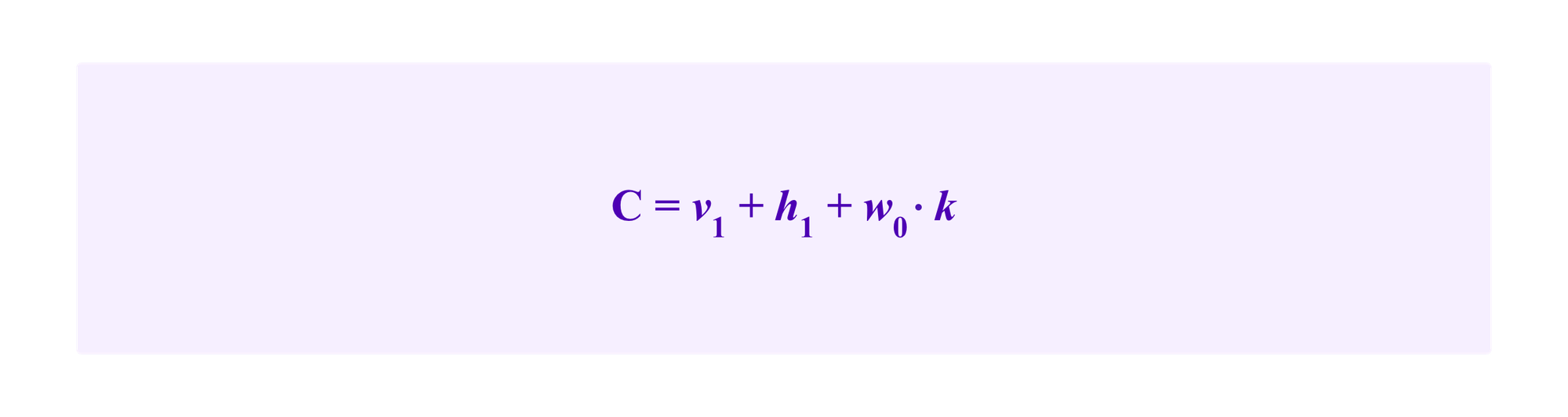
So then this inequality turns into

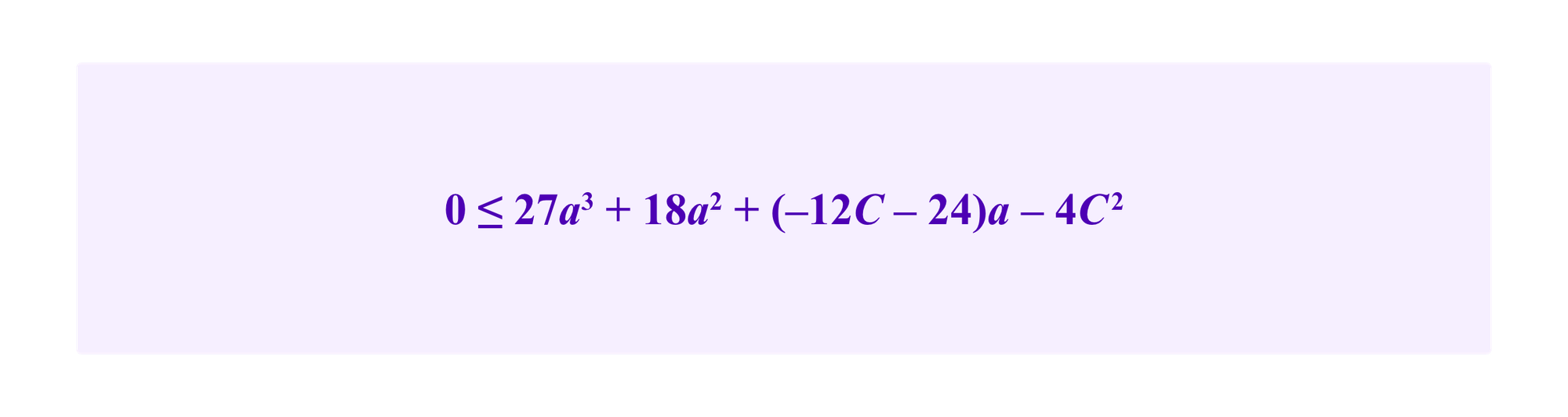
which one can solve using the cubic formula to see that the internal attack is more effective, at least under our assumptions, for

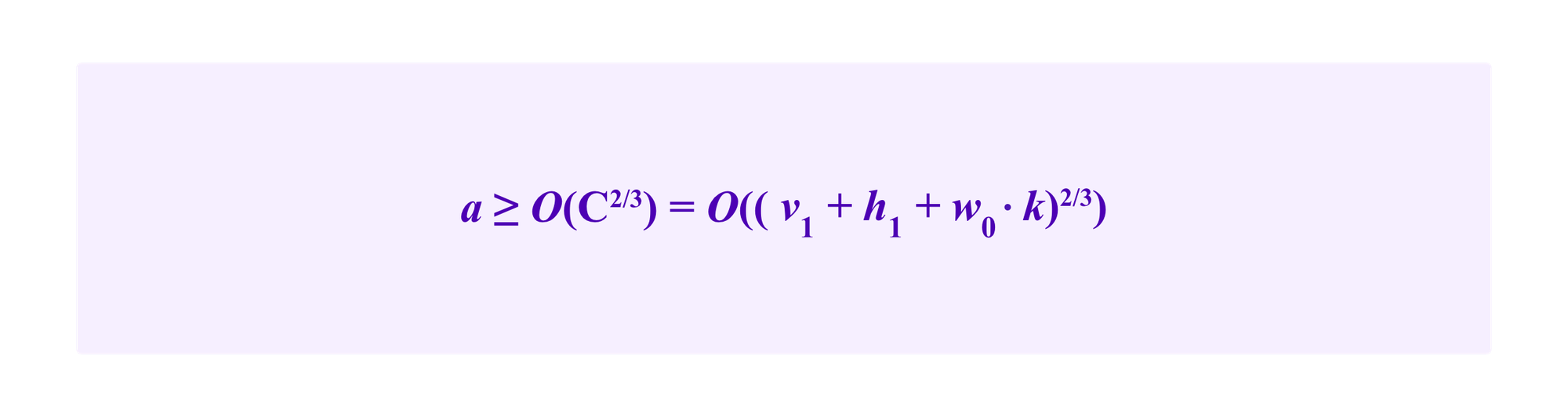
So this gives the sense that, when ca is still quite small, the attacker will put most of her resources in adding edges to ca but then once she passes a threshold that asymptotically goes as the quantity above, she will mostly put her resources into the interal attack.

Allocating resources between clusters

Up to this point, our attackers have just attempted to manipulate the clustering of the graph of users and SBTs. However, there is another set of choices that the attacker, in both Quadratic Funding and in Kleros, that factor into an attack :

• In Quadratic Funding, what contributions a1,...,ak does the attacker make using profiles that she may have that have been grouped into one of the clusters c1,...,ck.
• In Kleros juror drawing, what stakes a1,....,ak does the attacker make using profiles that she may have that have been grouped into one of the clusters c1,...,ck.

Note that in both cases, if the attacker has multiple Sybil profiles that have been clustered into the same group, it does not make any difference in the formulas for Quadratic Funding nor for Kleros whether she contributes with/stakes using one or the other profile.

In both cases, we take

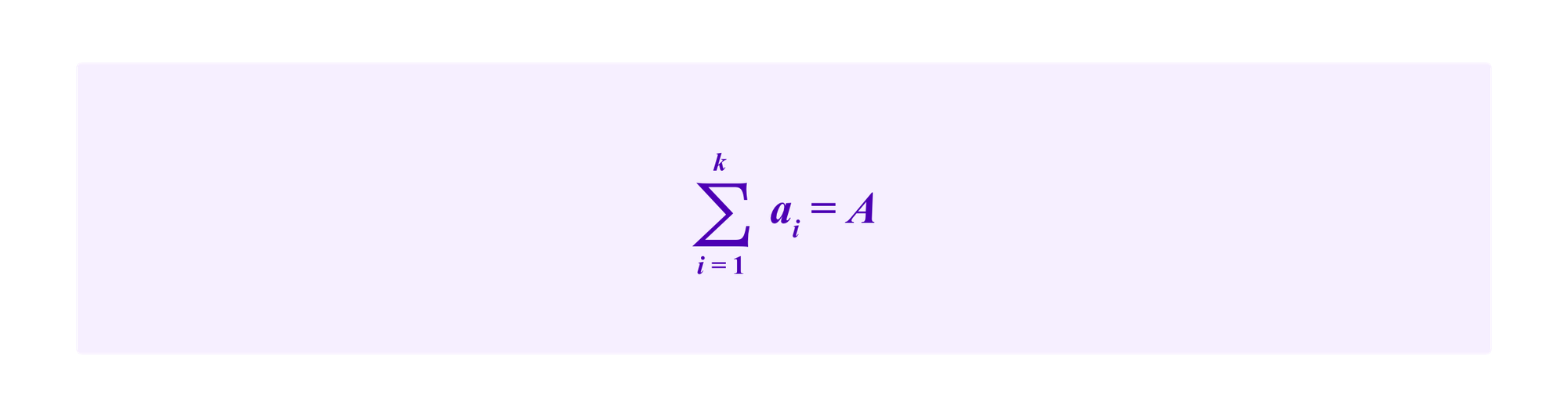
to constrain the attacker to some total amount of bounded resources. Similarly, denote by hi the total allocation by all honest parties in group ci and we denote

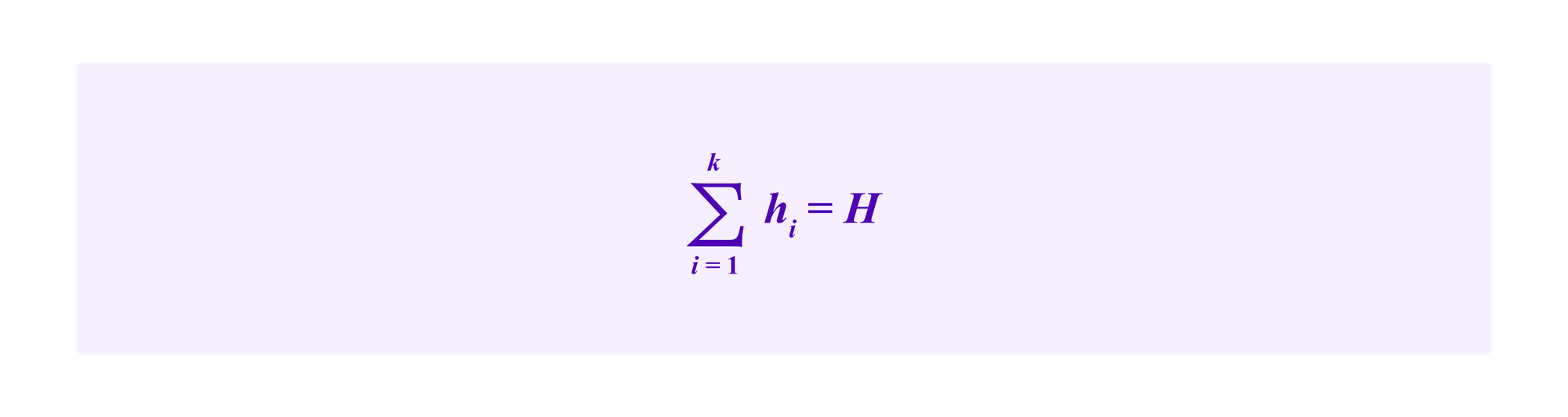
Then, one can think of the types of attacks that we have considered up to this point where the attacker attempts to alter which clusters are chosen as a setup phase where the attacker tries to give herself the most favorable conditions for then allocating her resources between those clusters.

The clustering determines which honest parties are in which clusters and hence how the honest contributions/stakes are distributed and whether the attacker has any Sybil profiles in a given cluster.

Up to this point we have suggested that the attacker attempts to manipulate the clusters to separate out clusters ca in which only she has profiles to make her profiles in those clusters seem like a distinct viewpoint that deserves extra weight. The extension of this logic is that the attacker wants to put her resources in clusters where there are little to no resources from the honest parties.

This approach turns out to be optimal for attacks against Quadratic Funding. Indeed, maximizing the amount of subsidy that can be extracted from the system

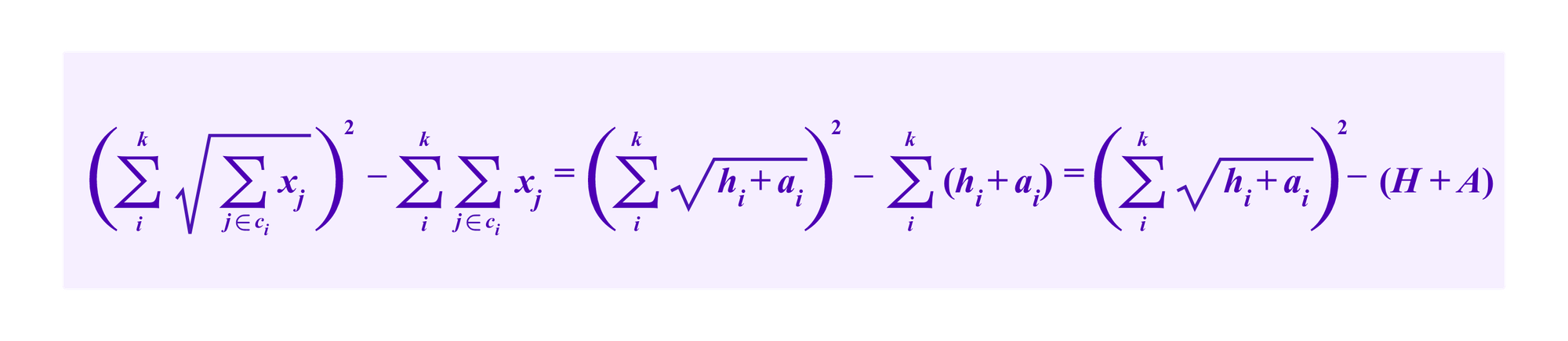
is equivalent to maximizing

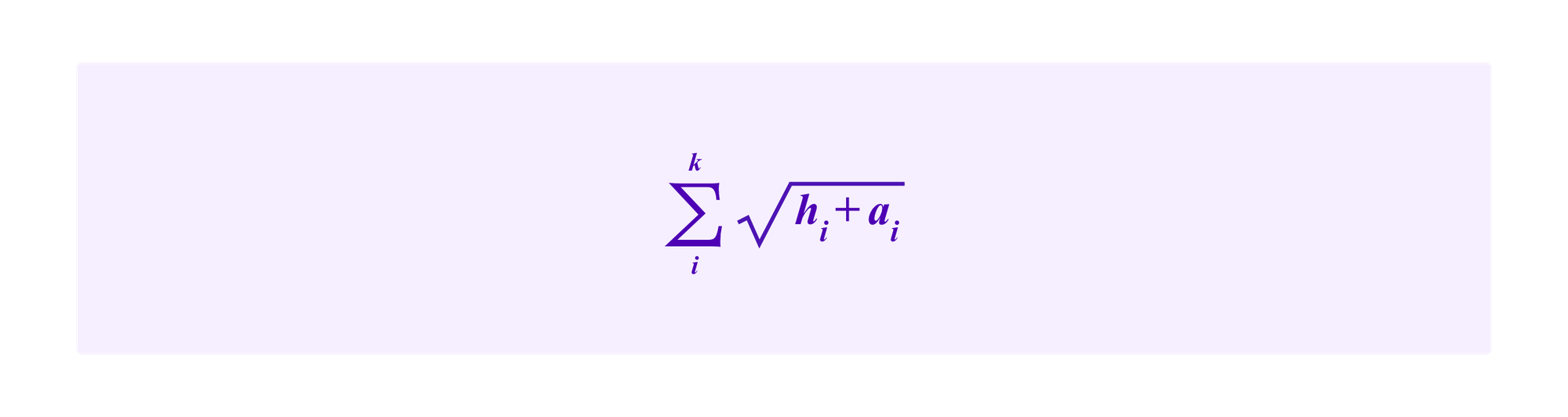
which one can see by a straightforward optimization argument is done when the ai are chosen so that

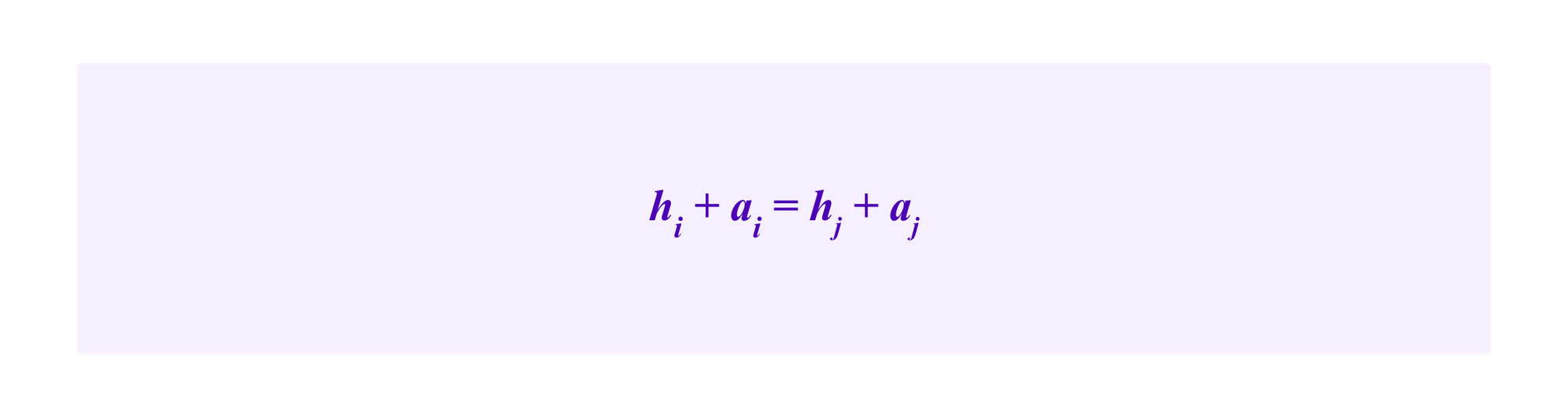
for all i and j, to the degree that the attacker has enough resources for this to be possible. Namely, it is the attacker's interest to have the clusters have stakes that are as uniform as possible.

This strategy turns out to not always be optimal against Kleros juror drawing. Consider an example where there are three clusters with honest allocations of 5, 1, and 0 respectively. Then the attacker decides whether she wants to allocate 4 to the second or the third cluster.

In the context of quadratic funding, the attacker is better off having her resources be in the third cluster based on the argument above. We see that this extracts a larger subsidy:

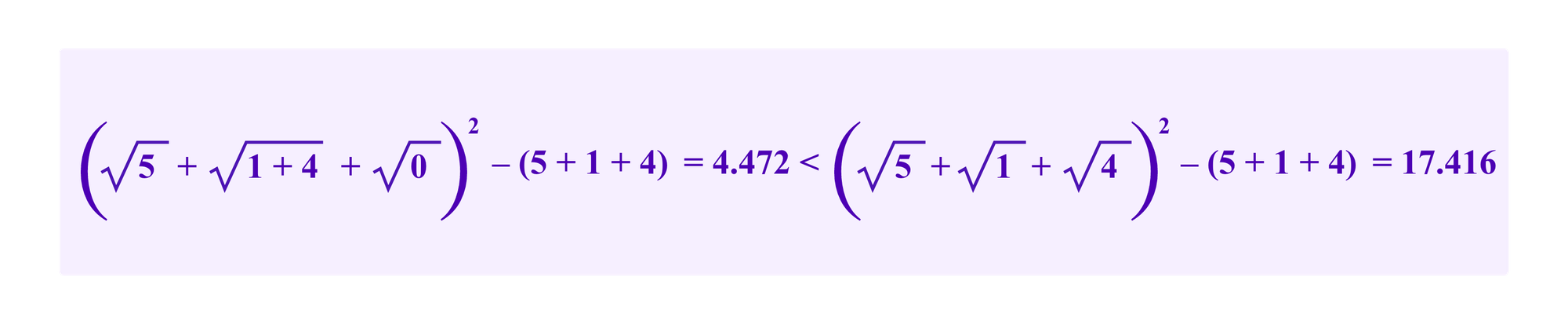
However, the attacker's drawing weight in Kleros juror drawing is higher if she stakes in the second cluster:

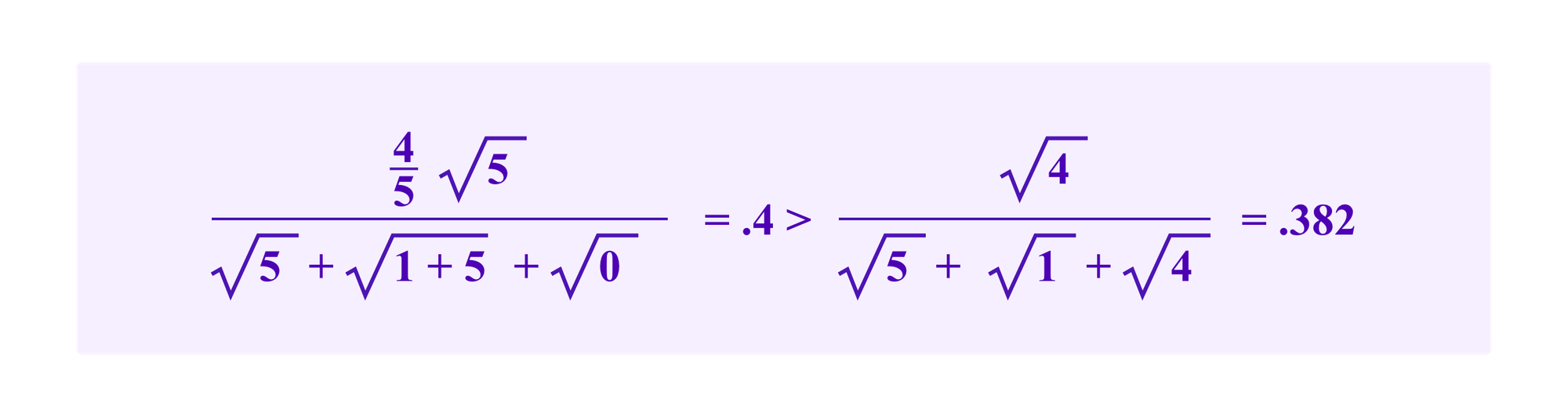
In Kleros juror drawing, the total drawing chances add up to one and the attacker improving her chances is the same as decreasing the chances of others. So she has a tradeoff between separating her stakes into clusters with little total stake so that her own term in

is greater and staking in clusters where other users are already staked so that their contributions in those clusters count for less.

One particular strategy that the attacker could use if she is capable of breaking the social layer sufficiently to obtain at least one profile in each cluster is to stake

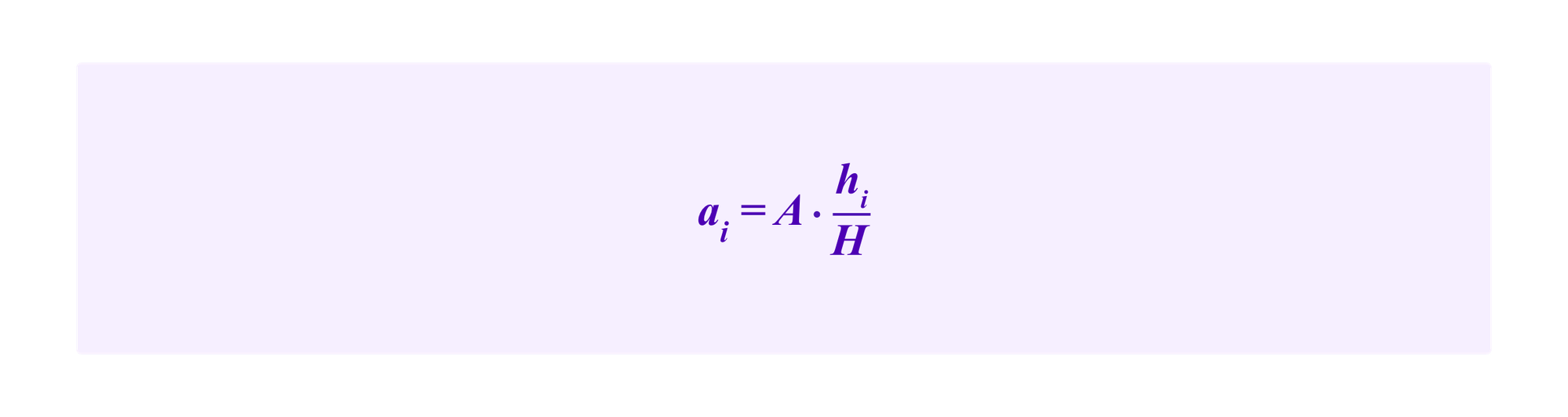
in each cluster. Then the attacker's total drawing weight is given by

Hence, in the scenario where the attacker has more or less completely broken the social layers of defense we have the unsurprising result that the attacker can obtain at least

A/(H+A)

percent of the vote. Namely, the attacker can obtain at least the same drawing weight that she would have had in a pure token weighted draw such as that used in Kleros 1.0. With some other distribution of the stakes the attacker may be able to obtain a greater weight.

Consider an extreme scenario where, among the k total clusters, the attacker has managed to separate off k-1 of them so that only she has profiles and is able to stake in these clusters. Then there is only one remaining cluster that contains all of the honest profiles where we assume that the attacker also has at least one profile and is able to stake.

The calculation to opitimize how much the attacker should stake on each cluster is then very similar to a calculation we perfomed in the previous blog article on how an attacker should distribute her stakes when attacking a weighting system we call “SBT-CM” which attempted to parallel the cluster match quadratic funding mechanism discussed in Miller, Weyl, and Erichsen.

This gave us the following table of how much stake an attacker must control to take over more than half of the voting weight in a court as a function of the number of clusters.

We see that if there are only 1 or 2 clusters, then indeed the attacker is incentivized to place some of her stake in the cluster with the honest participants in order to dilute their weight, even though there is less total stake in the clusters she controls. However, for k >= 4 the attacker manages to optimize her weight by placing all of the stake in the corrupted clusters and not staking in the cluster with the honest participants.

This might suggest a relatively small choice of k, maybe between 3 and 5 so that even in the worst case attackers need to have a large percentage of all PNK. Note that one might use a larger k in courts that are lower in the Kleros appeal tree as those courts can depend on the appeal courts to provide 51% attack resistance.

However, the more a court is specialized, the less likely it is to have a collection of SBTs that are relevant that can be used in clustering. Thus, it is somewhat regrettable that the appeal courts, where spectral clustering could add the most value in producing diverse juror panels are also courts where it is least appropriate to use these techniques with more than a few clusters due to concerns around attack resistance.

Running time

We will briefly touch on another point that is relevant in the choice of a juror selection mechanism for decentralized systems such as Kleros. In decentralized systems where calculations have to be repeated by many actors, one is somewhat constrained in the resources that a calculation can be allowed to take.

Kleros 2.0 is on the Arbitrum rollup, so that offers lower cost computations than on Ethereum mainnet, but there are nonetheless limits on what can be done economically.

Spectral clustering has a running time that is cubic in the number of vertices of the graph being considered. As we considered graphs where the vertices correspond to the users and the SBTs, this gives a running time of

O((number of users+number of SBTs)^3)

Moreover, there are the questions of how often this algorithm must be run, how much of it needs to be on-chain, and who pays the gas cost for it.

In Kleros 1.0, the drawing mechanism is designed so that a juror can adjust their stake using the setStake() call in O(log(number of users)) complexity and then jurors can be drawn also in O(log(number of users)) complexity.

So anytime an individual user wants to interact with the staking and drawing process, the amount of gas required from them does not grow too much with respect to the number of users, allowing for the system to scale well even if there is significant growth in the pool of users.

On the other hand, using spectral clustering techniques, if the graph of SBTs changes, what the clustering algorithm sees as the most relevant features to cluster based on can shift, resulting in a very different set of clusters. 

This means that a few changes to which SBTs users have could require one to update the drawing weights of essentially all users, as for each user the collection of other participants that go in the same square root as them will have changed. If there are many users, this could result in excessive computational requirements.

Note that if a user’s stake changes but the graph of SBTs stays the same, then we can update users' chances of being drawn

as follows. The contract can store

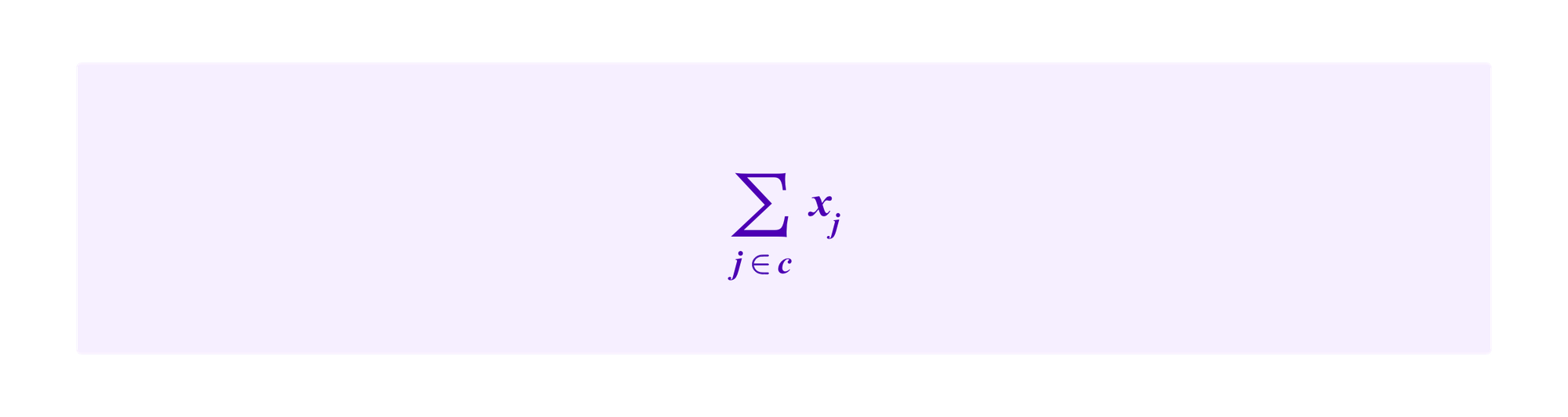
for each cluster c as the number of clusters will not be very large. Then, if a user changes a given value xj, the transaction called by the user to do so can update the corresponding sum in O(1) time by subtracting off her old stake and adding the new stake. 

Then, the system also can efficiently compute the denominator of the users' chances of being drawn

This is in some sense a weighted total stake. So then the drawing mechanism can convert a random value into a point on the interval between 0 and

This determines what cluster the juror that should be drawn is in. Then by having separate lists of the stakes of the jurors that are in each cluster, one can use an algorithm similar to the algorithm used in v1 to efficiently determine the appropriate juror.

Of course, one also needs to adjust the drawing odds for changes in users’ SBTs, at least periodically. Note that even though the off-chain running time to perform spectral clustering may be cubic, one cut down the computations that actually need to be provided to the contract as follows: 

• The contract can keep track of the (unnormalized) graph Laplacian, which is essentially the same as keeping track of the matrix of which users have which SBTs. This requires O((number of users+number of SBTs)^2) storage, but the entries of a given user can be updated in O(number of SBTs) when she calls setStake().
• Anyone can provide the contract with the eigenvectors and eigenvalues of the graph Laplacian L (appropriately normalized or not) using O((number of users+number of SBTs)) gas.
• A challenger who notices that there is an error in a submitted eigenvector Xi and eigenvalue ti can point out to the contract a coordinate j where the eigenvalue and eigenvalue do not give the correct value. The contract can then multiply the jth row of L by Xi and compare it to ti*Xi to check if there is indeed an error. If one is using the unnormalized graph Laplacian, then L is already in storage from the first step. If one is using the normalized graph Laplacian then it is straightforward to get the row we need with one extra matrix multiplication. All of this requires O((number of users+number of SBTs)) gas.

So this interactive update process only requires O((number of users+number of SBTs)) gas. If the number of users grows, this could represent a lot of gas for any one individual user to pay to update her drawing odds. Unfortunately, this procedure does not seem to naturally split up into pieces that can be integrated in the setStake() transactions so that the gas costs could be shared over these transactions.

However, this is ultimately at the scale of the amount of gas that the contract would have to use per unit time anyway as each user can be expected to periodically issue a setStake() transaction. So it should be viable to just have one user come along periodically to initiate this global update on how users are clustered based on any updates they have made to their SBTs. Such an actor could be incentivized by a grant from the Kleros DAO for example. The rest of the time, users' setStake() transaction update their stake but not their cluster assignment. 

Further work might consider improvements to how this calculation is managed by the contract. For example, perhaps one could provide a zk-proof of which jurors should be drawn when calling drawJurors() that proves the result of the computation to the contract without having to perform it on-chain. As many of the conditions that go into the spectral clustering algorithms are already in the form of matrix equations, namely systems of linear equations, this is a problem that may lend itself well to zk-tools like PLONK.

Conclusions

We have explored some of the questions that arise when one considers using spectral clustering techniques in decentralized settings. We have sketched at least one approach that might be viable: using the normalized spectral clustering that approximates NCut after modifying the social graph to add a common neighbor.

Nevertheless, these ideas seem to be fairly subtle. The fact that many natural approaches run into problems should give one pause that there might be other problems that we have yet to identify.

Open Research Questions

• Are there other versions of this idea that are more adapted to attack resistant decentralized systems? We suggested taking a normalized spectral clustering that approximates the NCut after adding in a common neighbor as this version of spectral clustering avoids various issues we found with other versions, but there may be approaches that are better yet.
• Are there other approaches to clustering entirely that one might be appropriate for these applications?
• What is an optimal choice for the number of clusters the algorithm produces k? How might this choice depend on the use case?
• How can one make sure that the computational requirements and hence the gas costs of juror selection are reasonable while still preserving the advantages of these mechanisms.
• What are some other decentralized applications where these ideas might be relevant other than Quadratic Funding and Kleros juror drawing? What aspects of this research generalize to a common framework that covers all of these applications? For example, people have considered mechanisms that make use of social information for the dissemination of messages on social networks. While the formulas of those approaches don't immediately seem to lend themselves to the mechanisms of this article, maybe one can find interesting commonalities.