Research Topics in Kleros Juror Selection – Blockchain Identity, Soulbound Tokens, and Models of Attack Resistance

When Kleros 1.0 was launched in 2019, the Ethereum ecosystem lacked good, decentralized, blockchain-based identity tools. Ethereum users were only identified by their address, and any user could generate as many addresses as they wanted so that it would seem that their actions were being made by many different users.

In that environment, the Kleros smart contract needed some way of choosing the randomly drawn jurors from among users who are staked in the court to vote in each round of any given case. With the lack of a useful notion of blockchain identity, the only approaches available to make such a system secure were economic. Users stake tokens, and one can show economic security guarantees that based on the idea that a malicious party needs to obtain more tokens than the honest participants in order to attack the system.

Specifically, in Kleros 1.0, jurors are drawn according to the following process:

Model (S)

If n jurors are staked in this court with stakes s1,...,sn respectively, then the odds that a given juror i will be selected on any given draw are:

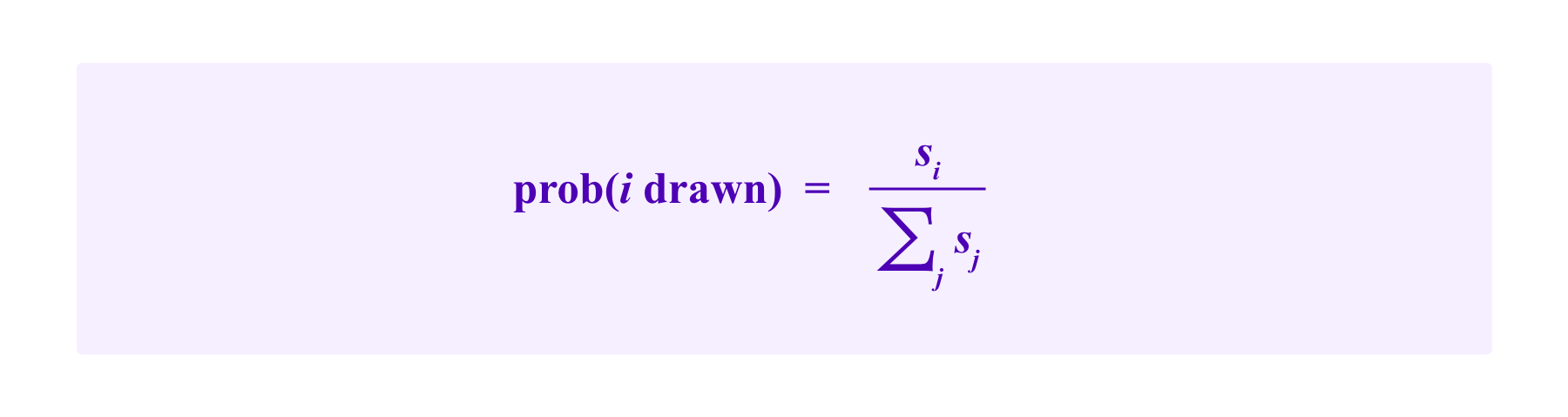
Note that this draw is "with replacement". So an individual can be selected for more than one of the juror spots in a given round and jurors' odds of being drawn do not change from one round to the next.

Without blockchain-based identity tools, basically any other rule to draw jurors would be exploitable by Sybil attacks. One could imagine building into the juror drawing mechanisms rules that limi each Ethereum address to being drawn at most once per dispute or that make the chances of jurors of being drawn grow sub-linearly as their stake increases to reduce the weight of whale jurors. However, users that wanted to manipulate such mechanisms could split their PNK up over many addresses. Indeed, dishonest users would have a disproportionate weight compared to honest users who did not split up their PNK over different addresses like this.

In the extreme case where all users have split up their PNK so that they each only have tiny amounts of PNK on many addresses, the smart contract can only see that there are many users with small stakes with roughly even chances of being drawn. Then one recovers the drawing weights of model (S) above.

Note that in this model, the threshold for an attacker to stake enough PNK to take over a court is clear. She would have to stake more PNK than all of the other jurors in that court combined so that, in a late-round appeal where many jurors are drawn, by the law of large numbers the attacker is reliably drawn for more votes than all of the honest jurors put together. We call this attack a “51% attack”, drawing terminology from similar attacks on blockchain consensus protocols such as Bitcoin and the initial Proof-of-Work version of Ethereum, specifically because the threshold for the attacker is to have more than 50% of some scarce resource that is used to determine voting weight, in this case PNK.

In the rest of the article, we will consider different models of drawing jurors that are enabled by obtaining Sybil-resistance from new blockchain-based identity tools. Particularly, generalizing our analysis of 51% attacks, we will consider what attackers would need to do in these different systems to take control of the court. The requirements to launch these attacks will no longer necessarily (just) consist of obtaining more than half of the staked PNK, though they generally require that the attacker(s) control a large percentage of staked PNK. Hence, we will refer to these attacks generally as “whale attacks”.

Proof-of-Personhood Protocols in Kleros Juror Selection

In the past years new blockchain-based, decentralized identity tools that expand the space of approaches one can take to Sybil resistance and whale attacks have become available. One important class of such tools are Proof-of-Personhood protocols, including Proof-of-Humanity (PoH) which was developed by the Kleros Cooperative itself. Recall that PoH achieves Sybil resistance by essentially having a curated list of human beings. Each human, when submitting themselves to the list, has to provide a deposit and submit video of themselves and if an existing profile on the registry is determined to be the same person the submitter loses their deposit. Disputes about whether a submission is a duplicate or whether it conforms to the requirements of the list more generally are arbitrated by Kleros.

Now consider a situation where one uses Proof-of-Humanity in the drawing of Kleros jurors. For example, a simple modification to model (S) that one could imagine would be to:

Model (H)

1. Require that in order to be eligible to be drawn, a juror's address must be registered on Proof-of-Humanity.
2. Draw jurors where the odds of i being drawn are given in terms of the stakes of Kleros users, except that this draw is “without replacement”. Namely, if an address is drawn once, it cannot be drawn again (say for example while drawing in the same appeal round of a given case), so each Proof-of-Humanity profile is limited to at most one vote.

How does this extra mechanism affect resistance to whale attacks? Well, if a whale only controls one PoH profile or if a cartel of whales only controls a small number of PoH profiles, then it is impossible for them to be drawn with the majority of votes in a large appeal. So this system would not be vulnerable to whale attacks at all.

On the other hand, imagine that a whale managed to break PoH and obtain a large number of profiles. Then the attacker could potentially be drawn for more than one vote, while all of the other, honest participants are limited to one vote per person. Thus, the attacker's stake is essentially drawn "with replacement" while everyone else's stake is drawn "without replacement".

What are the attacker's chances of being drawn for the majority of the votes in a given case using model (H), and how does this compare to the chance she would have if one used model (S) without PoH?

It turns out that this depends significantly on the distribution of stakes present in the court. If the stakes of participants other than the attacker are concentrated into a handful of whales, each time one of those whales is drawn and removed from the pool of stakers who can be subsequently drawn, the attacker's chances of being selected in subsequent draws goes up significantly. On the other hand, if the stakes of the honest participants are spread out over many participants who each only have a small amount staked, such a person being drawn and removed from the pool of eligible jurors for further draws has a minimal impact on the attacker's odds of being drawn going forward.

We can estimate the size of this effect more precisely. Recall that using model (S) where jurors are drawn with replacement, the probability that a participant that has a proportion p of the stakes is drawn k or more times is given by a binomial tail bound of:

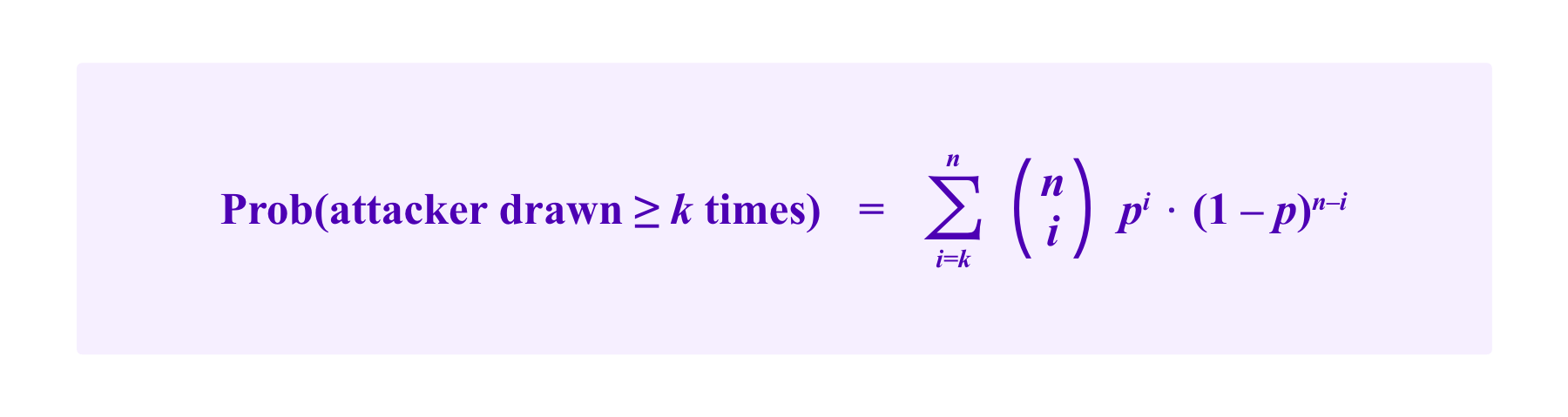
Now suppose that an attacker has a proportion p of the stakes, some collection of one or more whales collectively has a proportion u of the stakes, and all other participants have at most a proportion q of the total stake each.

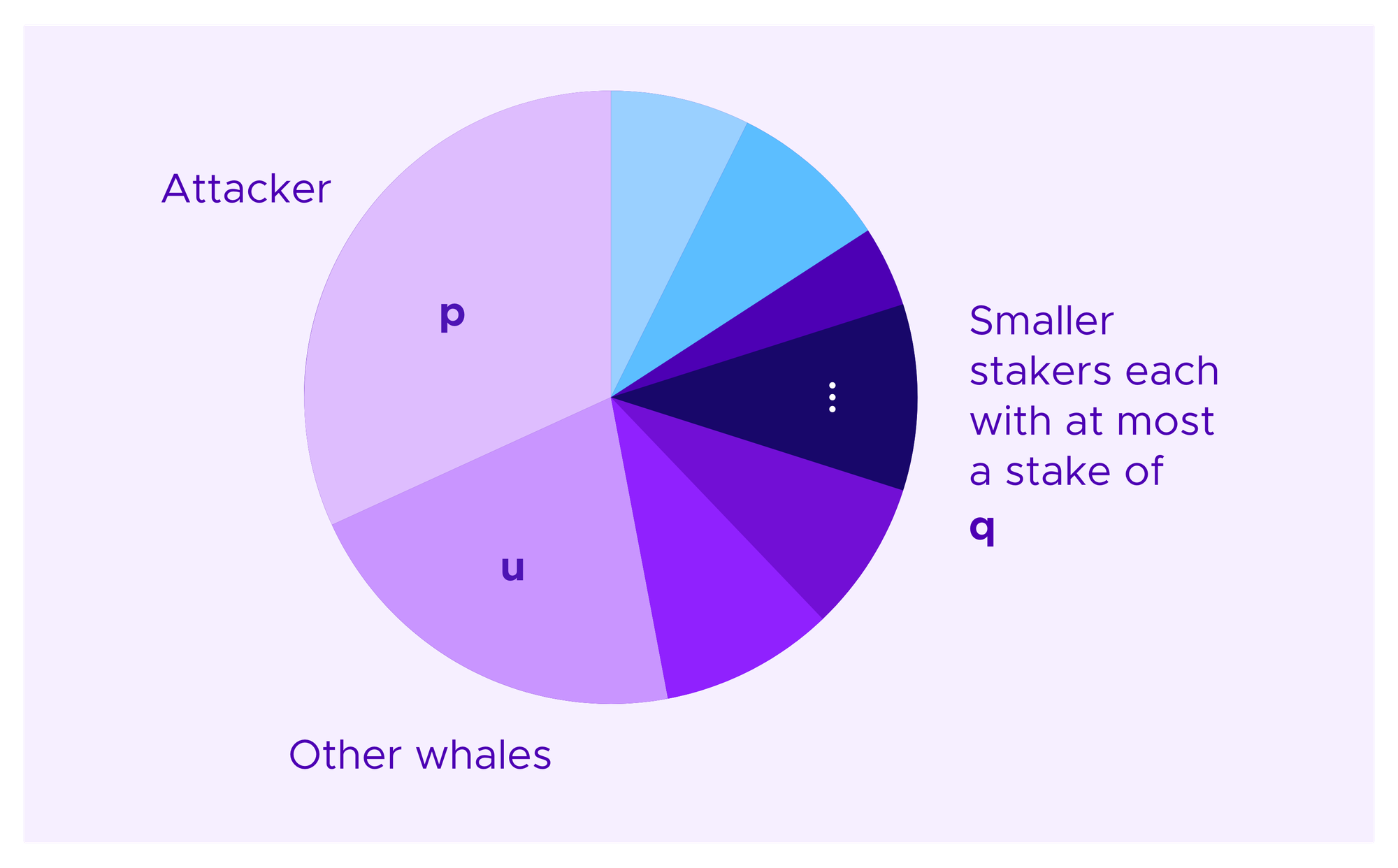
Denote by st the stake of the tth honest, non-whale participant to be drawn. Then, a crude bound on the attacker's chances of being drawn a given number of times under model (H) that one can obtain by simply throwing out the chance that any of the other whales are drawn and taking the worst case for the order in which the attacker's votes are drawn is given by:

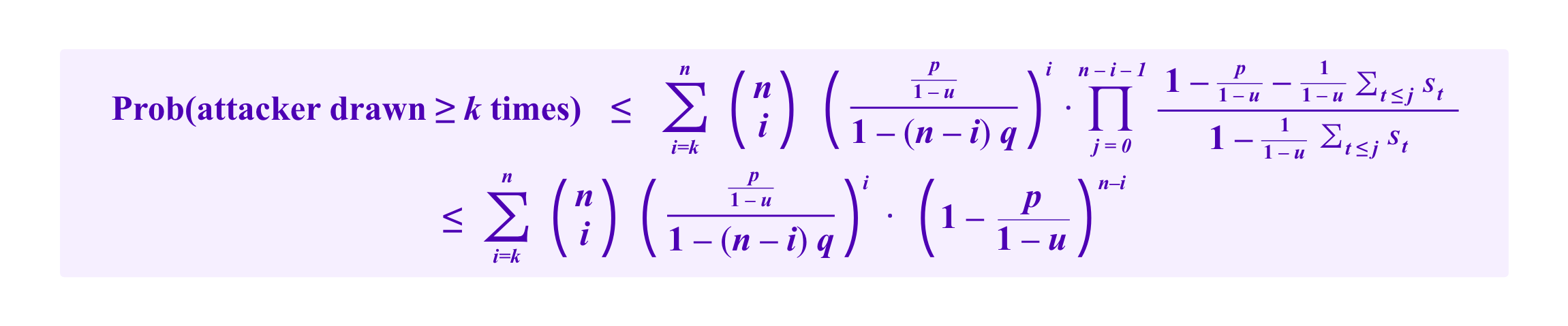
If one wants a first approximation for how resistant a given distribution of stakes is to whale attacks, one can use this inequality adjusting u and q to try to get the best available bound.

Note that as u and q tend to 0 one recovers the distribution for the attacker's number of draws under model (S). In fact, if q is small, namely stakes are distributed over many small participants once one excludes a small number of whales, then the upper bound corresponds to the attacker's votes being distributed as under model (S) but where the attacker has a proportion of p/(1-u). In particular, in this case, one is still resistant to a whale attack as long as p/(1-u)<.5.

Then we have seen that the security model for model (H) is that the system is resistant to whale attacks if:

• the Proof-of-Personhood scheme is secure OR
• no participant controls a proportion of stake that one can calculate based on the observed distribution of stakers using the bounds above. If a proportion of u belongs to a small number of whales and the rest of the stake is split over many small stakers, this threshold is≈ .5*(1-u) of the stake.

Thus, if the stakes are spread out over a sufficiently large number of participants, the defenses of the Proof-of-Personhood scheme and of using PNK staking against whale attacks complement each other. The attacker would essentially need to break both in order to take control of a court.

Recap of SBTs

"Soulbound Tokens" (SBTs) represent another recent advance in blockchain-based identity that were introduced in the paper "Decentralized Society: Findin Web3's Soul" by Weyl, Ohlhaver, and Buterin.

SBTs are non-transferrable NFTs. As they are non-transferrable, the SBTs that belong to a wallet accumulate and attest to the actions that that wallet has taken over time. As with classic identity, these attestations can be both positive or negative. One might have SBTs that represent qualifications such as having completed an online course in HTML as well as negative SBTs that mark an address as having failed to pay back a loan.

Weyl et al argue that having richer forms of information about individuals could allow one to develop types of economic interactions that exist in traditional institutions but that have been largely absent from blockchain systems, such as undercollateralized loans. In their vision of SBTs, one could stop using a wallet to escape the negative SBTs that it had accumulated but only at the cost of losing all the positive SBTs on that wallet and having to rebuild one's identity again from scratch.

How SBTs are issued is a question that is not fully resolved in the Decentralized Society paper and is still a subject of study. Different blockchain protocols might award SBTs as one interacts with them, whether those SBTs are viewed by the wider ecosystem positively, negatively, or whether they are largely ignored. Institutions that award qualifications such, as the online HTML course, could issue SBTs directly.

One possibility that we have considered to use Kleros to award (some types of SBTs) would be to have curated lists where individuals claim to a given type of expertise. Then, if they are accepted onto the list they receive an SBT that corresponds to that expertise.

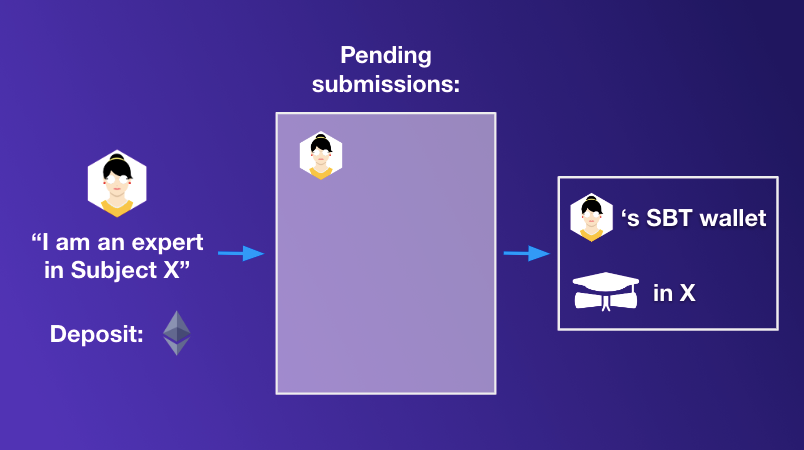
SBTs and Quadratic Funding

Before we continue our discussion of how SBTs could be used in juror drawing in Kleros, we will consider one concrete application of SBTs that Weyl et al introduce in the Decentralized Society paper, that is then expanded upon in this subsequent paper by Miller et al, which is the idea of using SBTs to weight contributions to quadratic funding schemes for public goods. This will turn out to have interesting similarities to how one can use SBTs in juror drawing.

Recall that quadratic funding as proposed by Buterin, Hitzig, and Weyl is a scheme for providing subsidies to candidats proposals based on the contributions of a group of users. If users 1,...,n make contributions of c1,...,cn respectively, the subsidy provided in (the most basic form of) quadratic funding is:

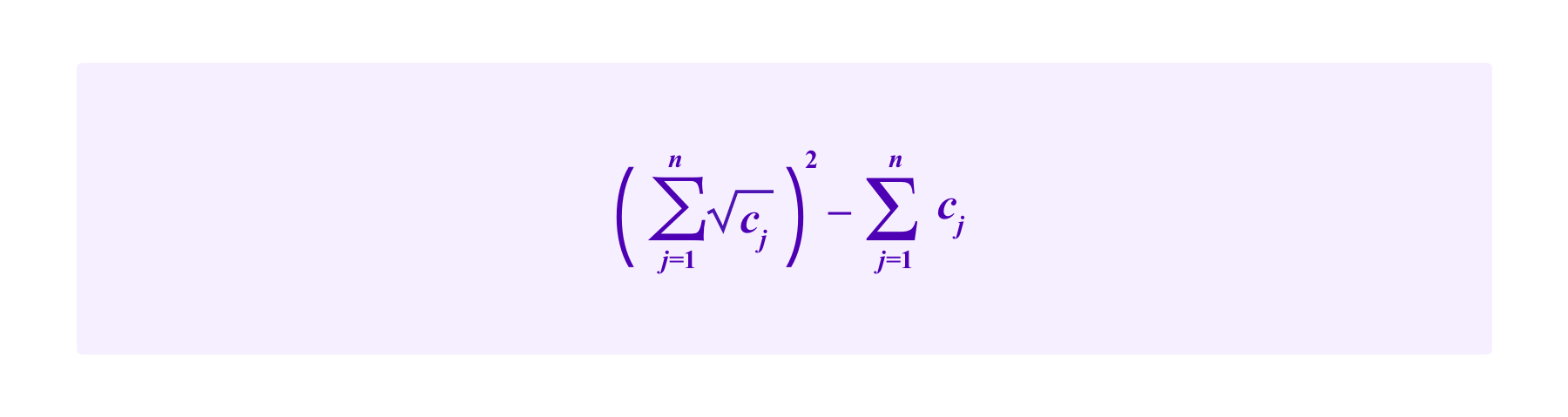
So then the total amount received by that project including the contributions is:

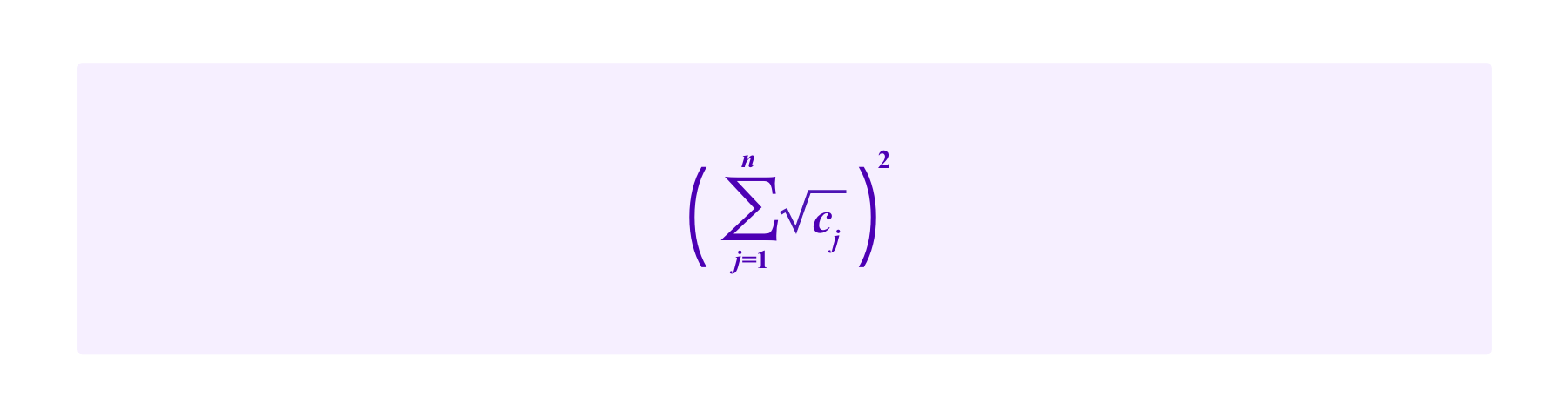
A key idea is that projects that are supported by many individuals receive more in subsidies than a project that gets an equivalent amount in contributions from a smaller number of individuals.

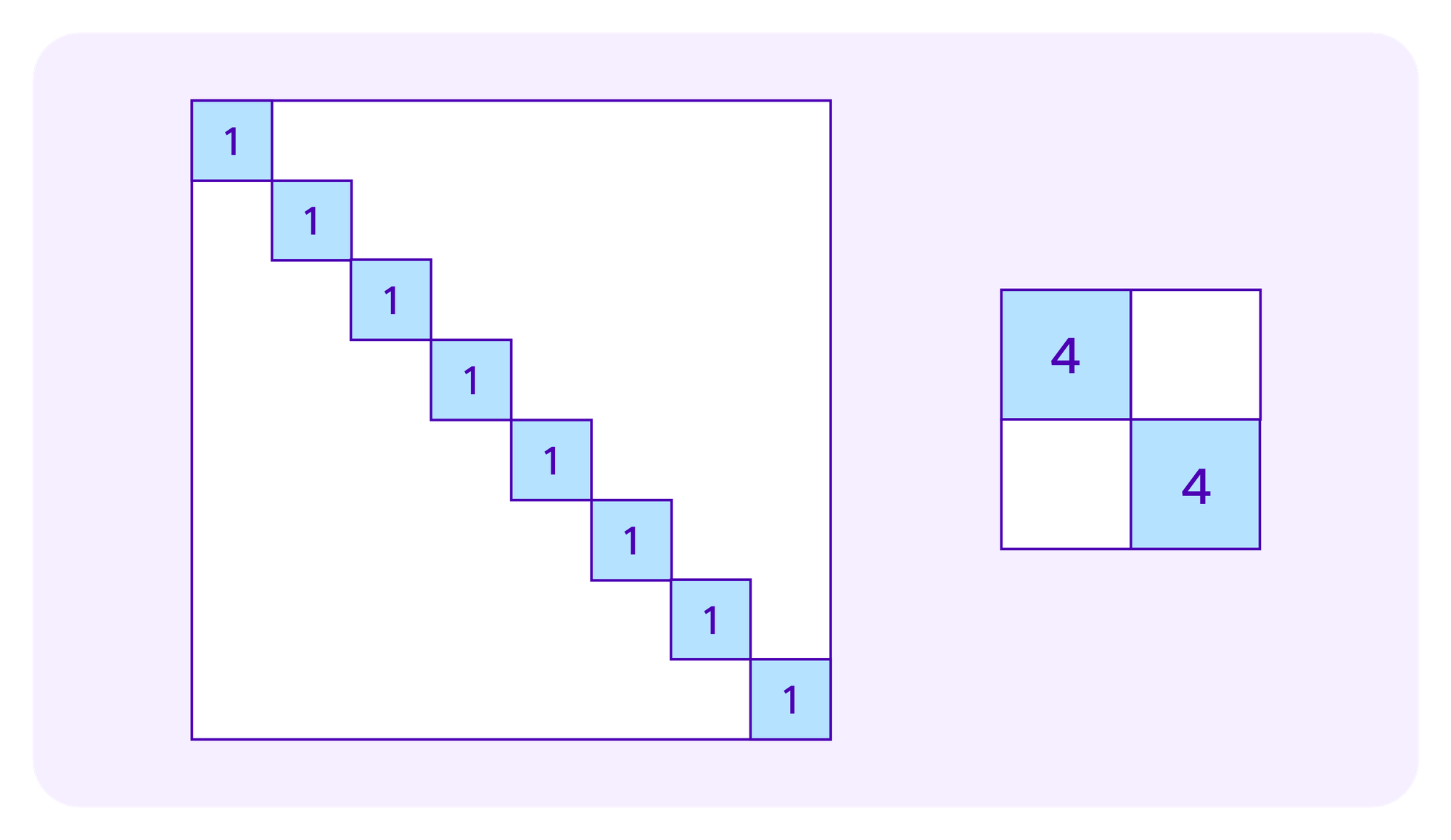
Then, Weyl et al consider how to improve upon this mechanism using weighting by SBTs. The idea there is that if lots of similar individuals (as measured by the SBTs they have) make contributions, this should result in less in subsidies for a project than if a lot of dissimilar individuals make contributions, funding a project accross different, very distinct groups. One rationale for this is that if people have similar backgrounds they are more likely to have some off-chain connections that would make it easier for them to explicitly collude on to which projects they provide contributions. Such collusion can be defended against with this type of SBT-weighting. Moreover, even if individuals are not explicitly colluding, projects that have support from different constituencies are more plural and are more likely to be valuable to the broader society.

One such weighting scheme that they consider they call the "Cluster Match". Here the idea is that if several contributors all belong to the same "group", their contributions should be put together under the same square root as if they were the same individual. One can use SBTs to get a sense of how individuals break into groups. However, generally people won't have exactly the same set of SBTs. So in Weyl et al's formulation of the Cluster Match, each individual belongs partially to several groups, one for each SBT she possesses.

For example, one might be awarding grants for making websites that are useful to a community. Then, some participants might have an SBT from completing an online HTML while other obtain an SBT that shows that they are experts in design. These two groups may have different points of view on what websites are valuable and the Cluster Match approach attempts to ensure that they both have significant weight in determining the matching funds. Some users may have both the HTML SBT and the design SBT, in which case they are treated as belonging partially to each group.

Denote by G the set of groups each of which is defined as possessing a given SBT and Ti as the set of groups to which a participant i belongs, so |Ti| is the number of SBTs i possesses. Again suppose a project receives contributions c1,...,cn by contributors 1,...,n respectively. Then the total amount of funding for this project including the subsidy given by the Cluster Match is:

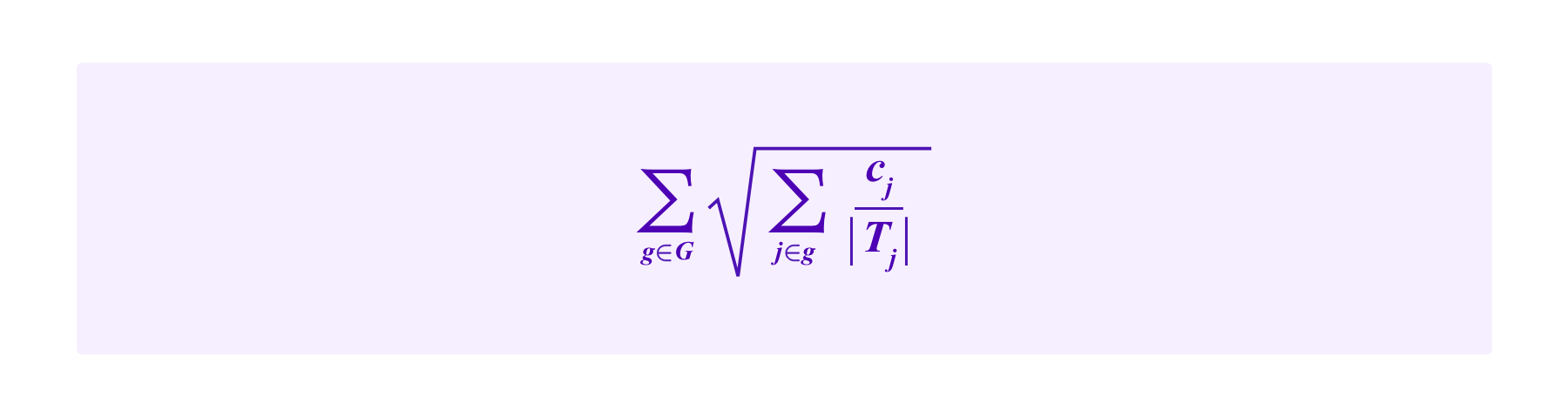
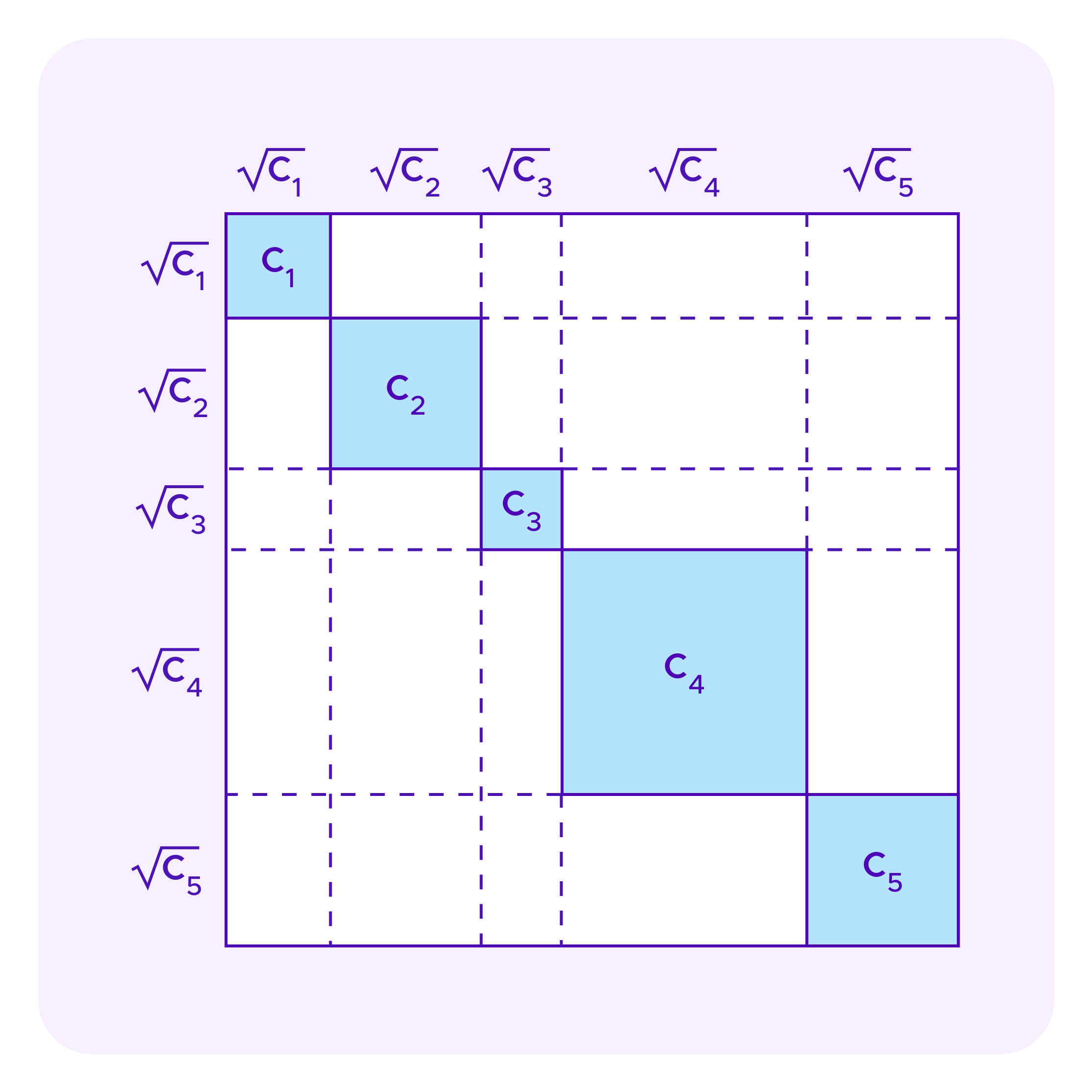
Many of the arguments of Miller et al consider the amount of growth one that can engineer in the white rectangles as one increases the size of the blue squares – namely, how much additional subsidy additional subsidy can one extract from the system relative to one's contribution. They are particularly interested in the interactions between increases in contributions from different participants to prevent groups of colluding contributors from being able to extra too much in subsidies.

SBTs and Kleros

A first, basic idea for how one could apply SBTs in the selection of Kleros jurors is to require an SBT that attests to a given type of expertise in courts where that expertise is required. In Kleros 1.0, users can stake in any court. However, if a court requires uncommon skills and an inexperienced juror stakes there, she is likely to frequently be incoherent and be penalized over time, encouraging her to destake from that court and stake in some other court that better matchs her skill set. By requiring that jurors in a court have an SBT indicating that they have required skills up front, one can complement this effect to make it that much more likely that jurors have the necessarily skills to judge cases.

The security model of such an approach is the same as that as of model (H), only now the only stakes that one considers are those that belong to jurors possessing the required SBT. Restricting to such a smaller set of potential jurors may be mitigated if appeals go to a court that does not require such an SBT; even if the jurors in the appeal court lack the required skills to evaluate the underlying case, they could invalidate a lower court ruling if it resulted from an obvious whale attack.

More ambitiously, one might consider several SBTs as being relevant to cases in a given court. For example, one could have a system where small business owners higher freelancers tasked with creating a website for the small business, and then any disputes about whether the websites meet the required specifications and are of adequate quality are decided by Kleros.

In the court that judges these cases one might have jurors with a "HTML expert" SBT and other jurors with a "design expert" SBT. Some jurors may have both SBTs, but there may not be enough such jurors for it to be viable for the court to require that any juror selected to judge these cases must have both SBTs. Nevertheless, one wants to draw the juror panel in such a way that one is likely to have both view points represented.

Generally, one can imagine a drawing mechanism that attempts to draw jurors with different SBTs, for example by giving jurors with rare SBTs more weight, with the aim of obtaining a juror panel with a variety of diversion backgrounds and skills. Such an approach draws on ideas in research in collective intelligence that diverse groups can sometimes outperform non-diverse groups composed of participants that are individually higher-performing.

In this direction of considering weighting based on many SBTs together, one might ask what the equivalent formula to the Cluster Match for drawing jurors might be. In some sense, one might expect the total "weight" of the stakes to be:

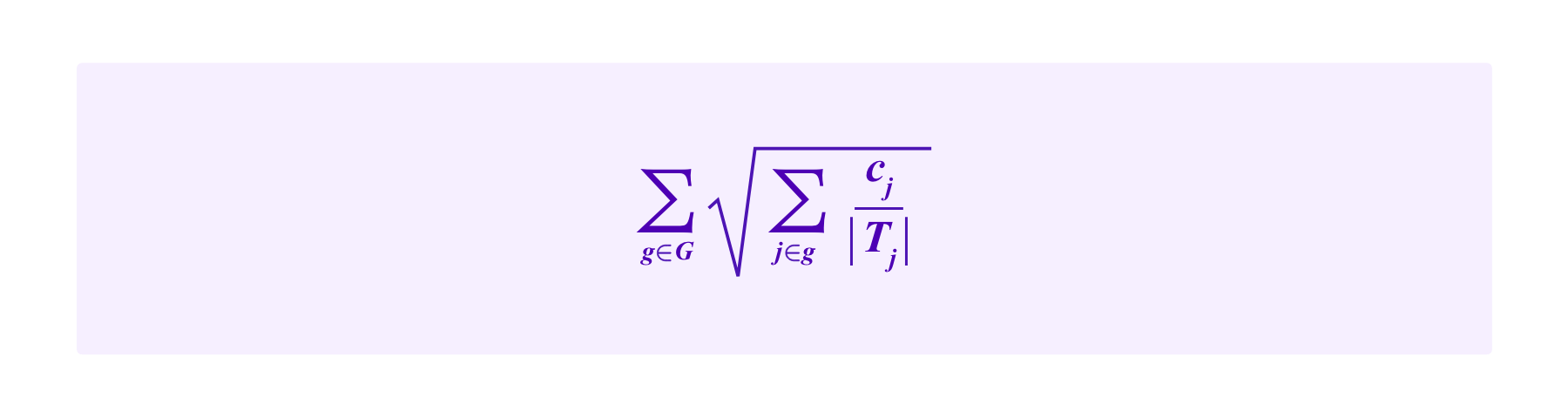
that should then somehow

1. be normalized to one to correspond to the total chance of all jurors being drawn and
2. divided up somehow into the chances of the individual jurors being selected.

However, note that

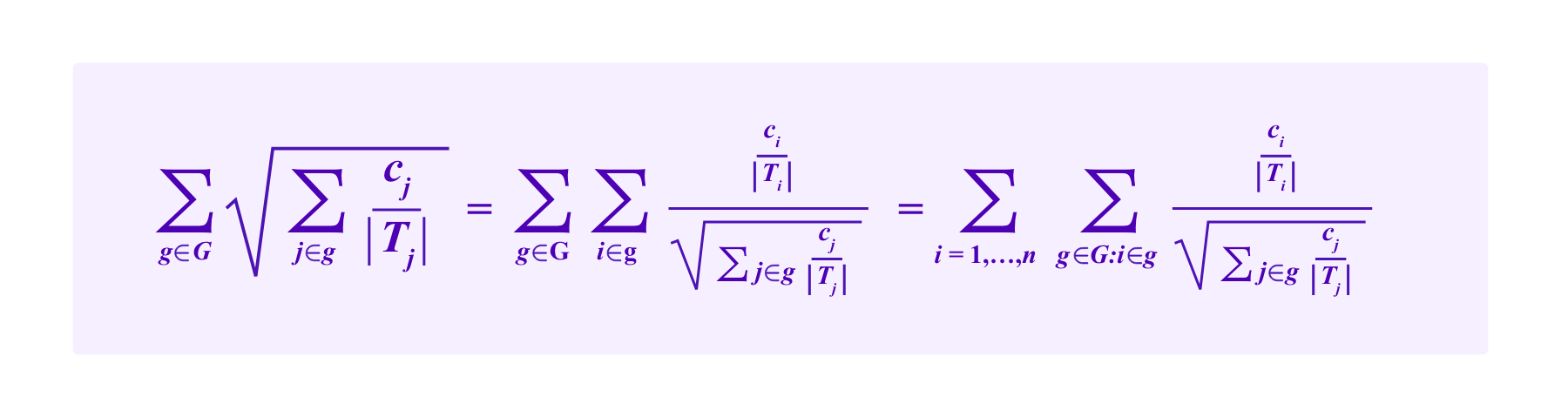
So one might think of i's portion of this quantity being:

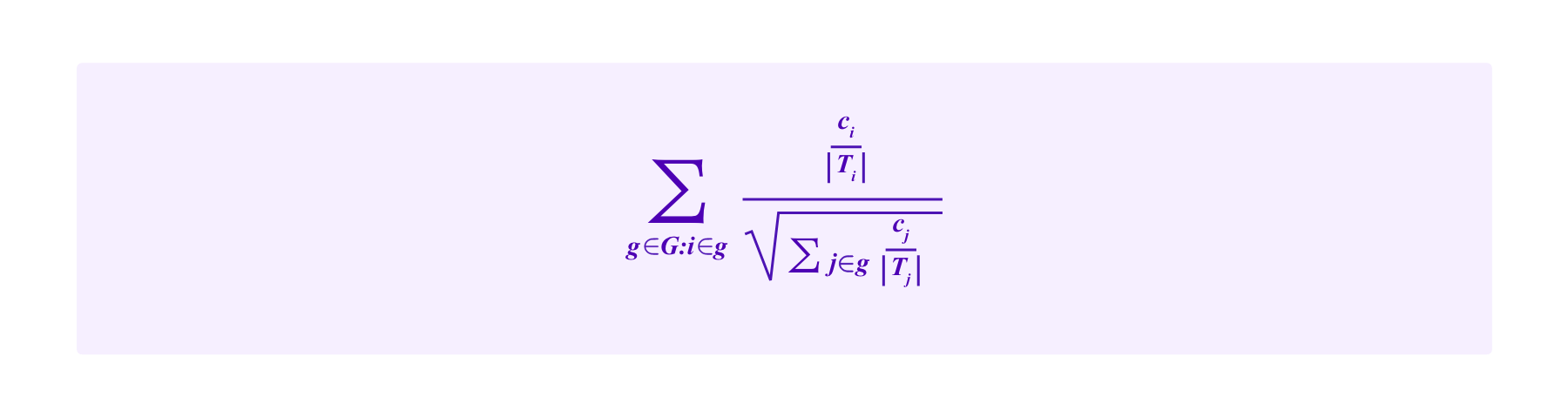
Namely, using this point of view, we are lead to the following drawing rule:

Model (SBT-CM)

The participant i has a chance of being drawn given by:

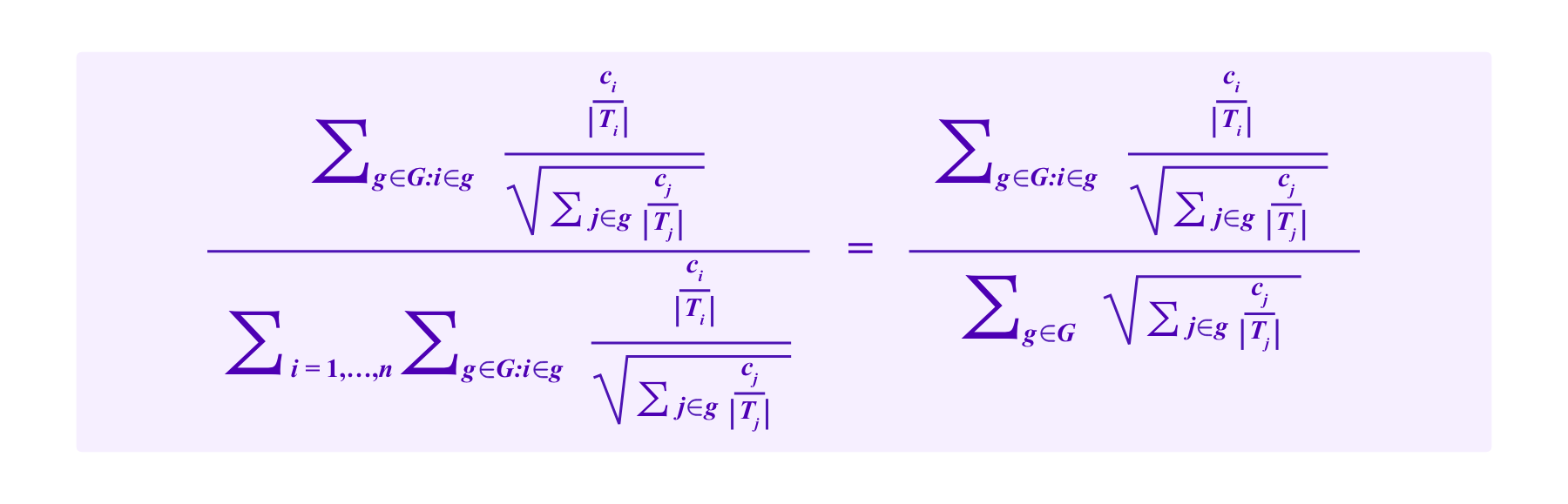
One can analyze these drawing formulas with similar "square diagrams" as those used above for quadratic funding. As a simple, initial example, suppose that G consists of three groups: G={1,2,3}. Suppose that all of the contributors to group 2 are being managed by a whale attacker, while the contributors to the other two groups are honest.

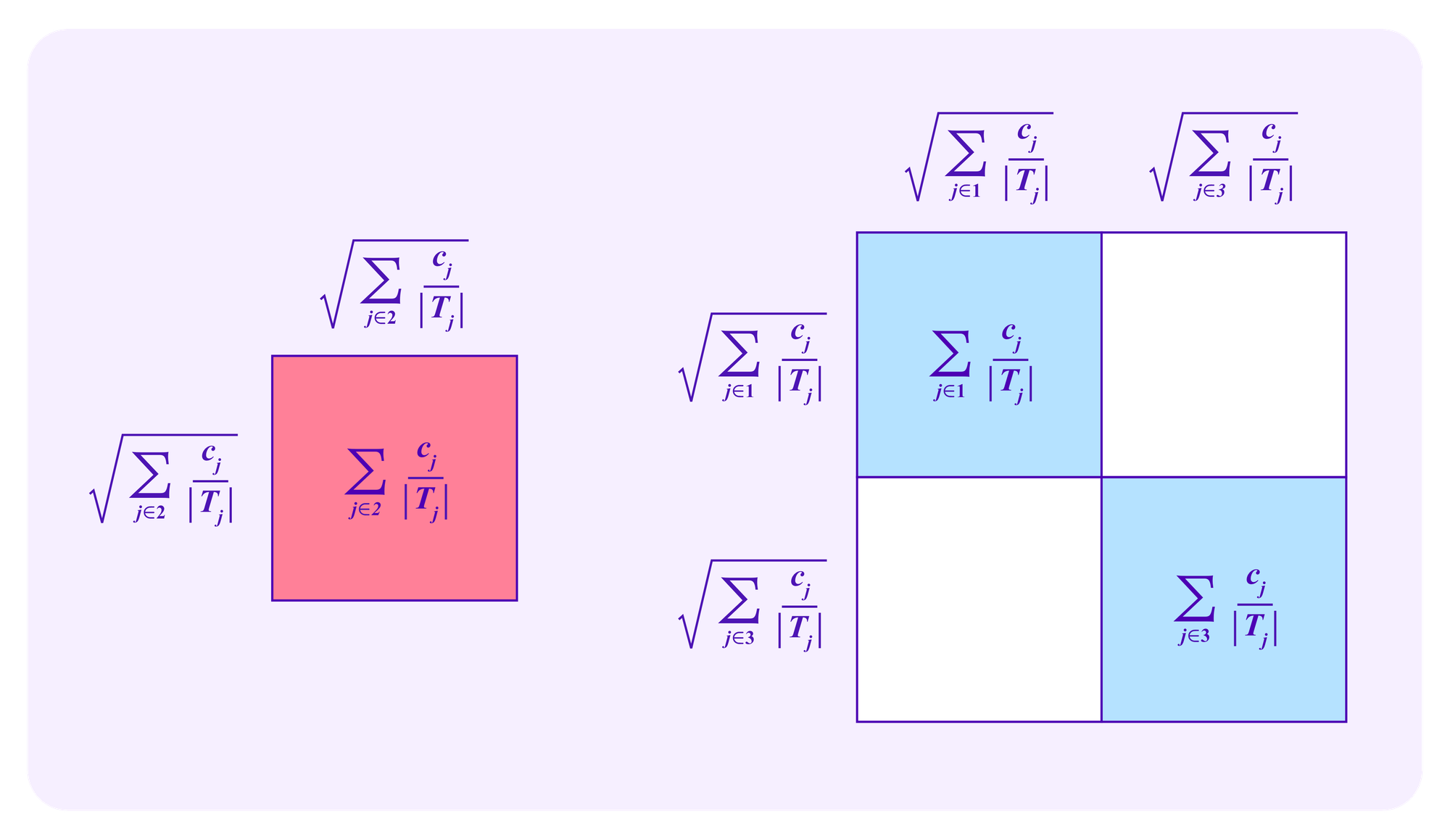
Note that, in this example, the attacker has greater than a 50% chance of being drawn on any given draw if and only if

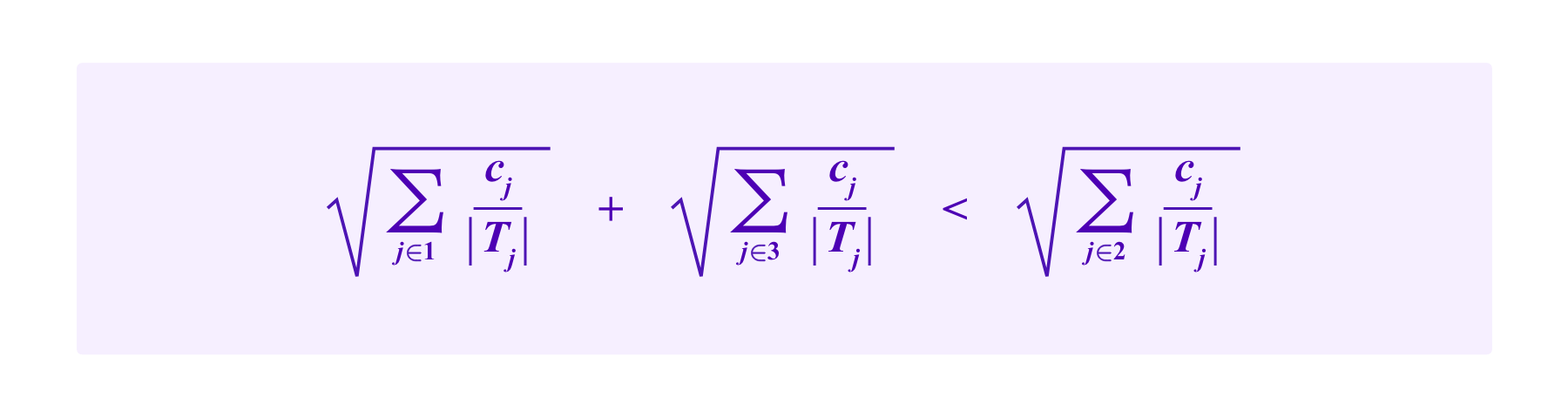
Namely, the attacker has greater than a 50% chance of being drawn if and only if the attacker's square is larger than the square consisting of the honest groups.

One might ask what the elements of these square diagrams represent in this case and how it compares to their meaning in the case of quadratic funding. For juror drawing, the blue squares on the diagonal correspond to the stakes of the users in the different groups, while the white rectangles correspond to the "extra" weight that the systems gives to participants from a set of diverse groups.

These pictures become more complicated when one considers that some stakers in a given group may be part of a whale attack while others are honest.

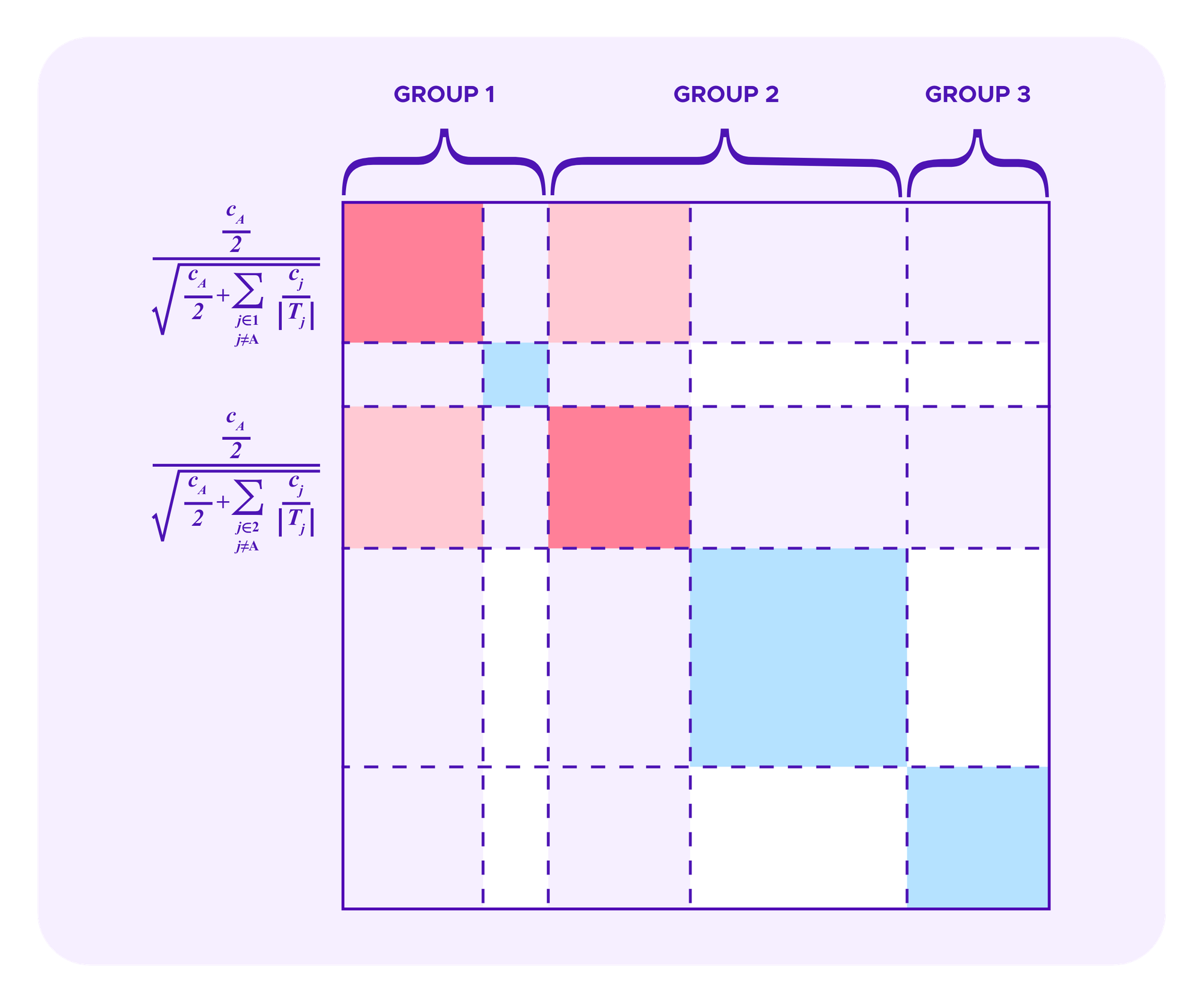
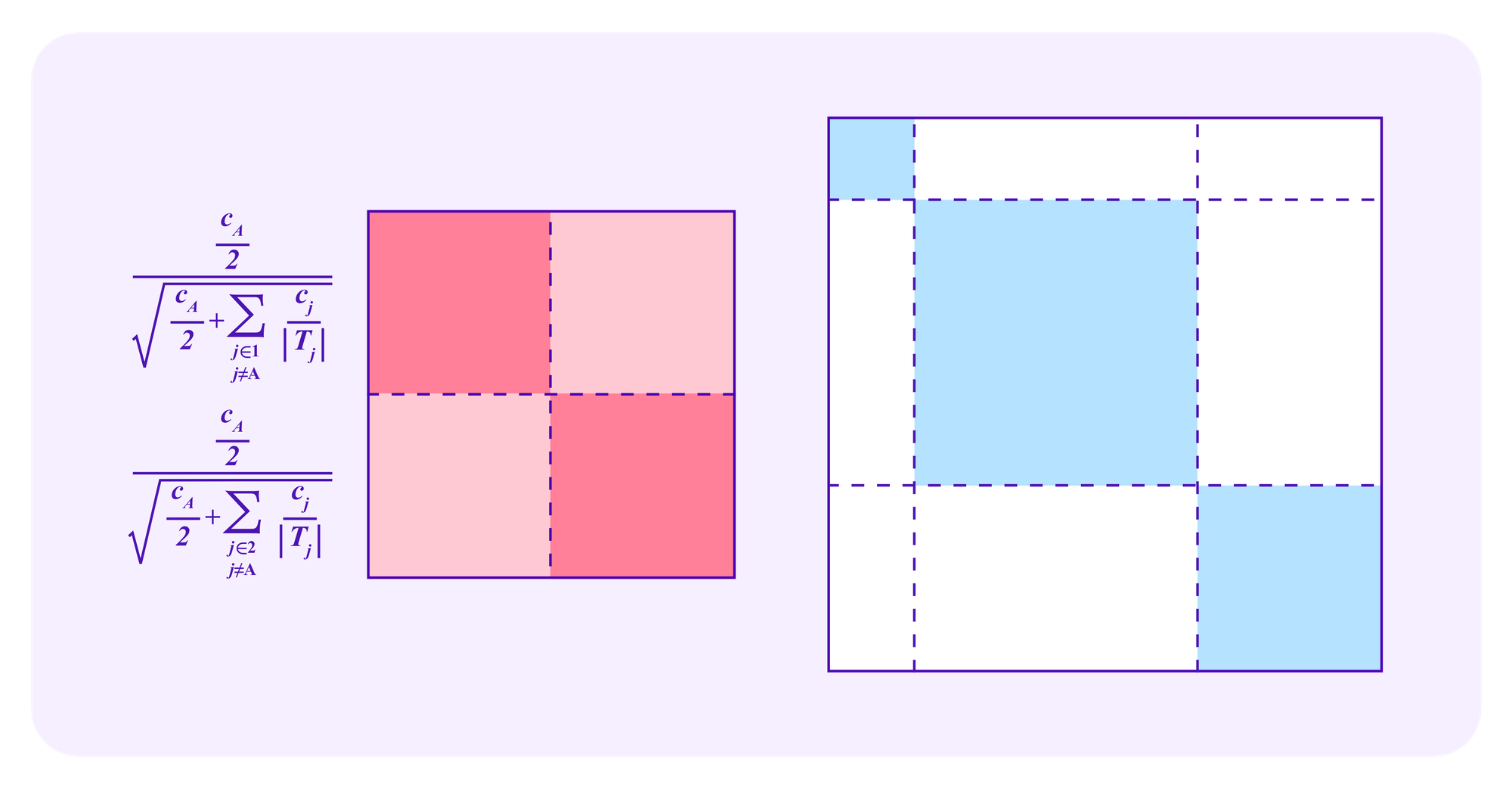
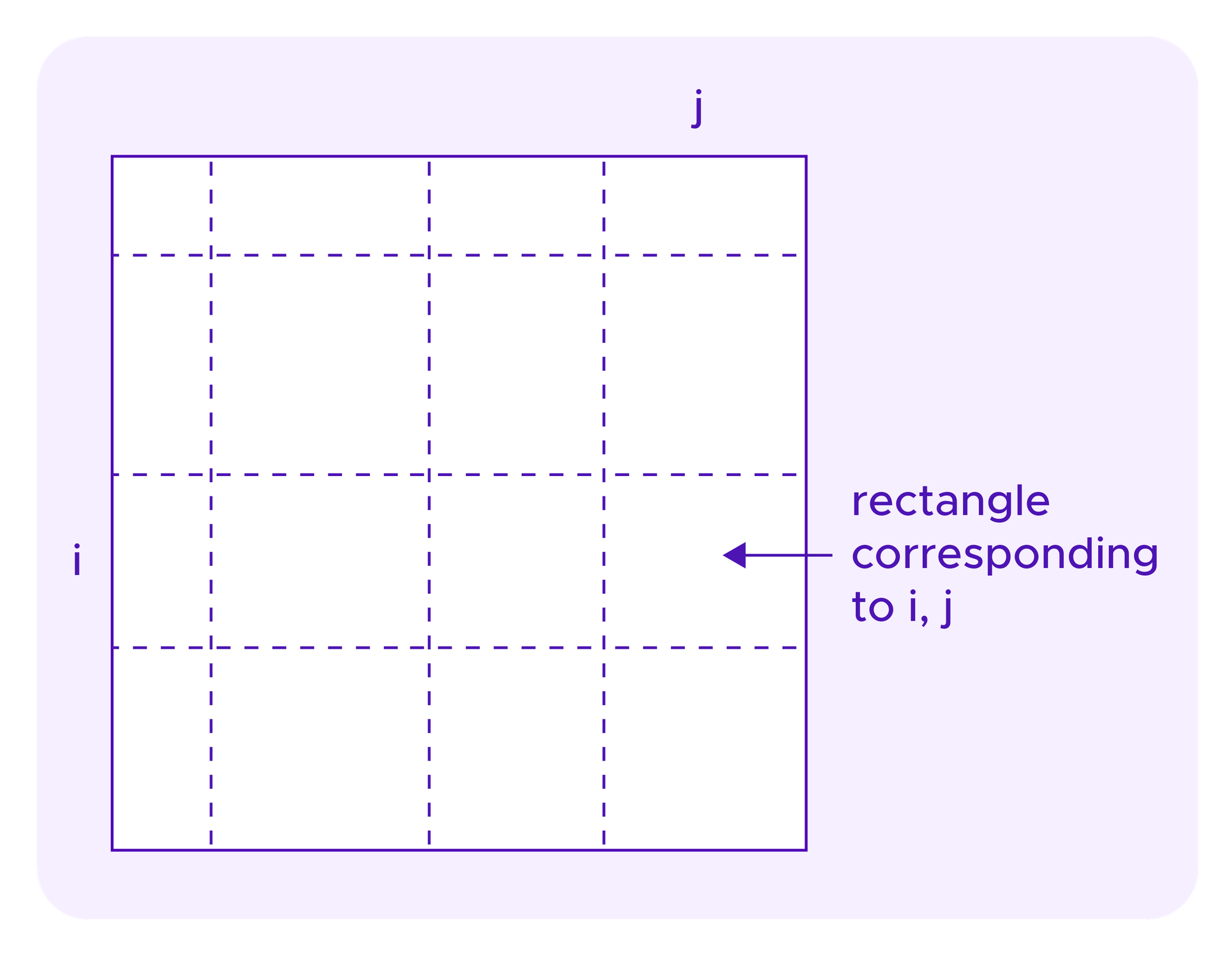
Recall again, as in the images above for quadratic funding, that each rectangle in these diagrams corresponds to some staker i in one dimension and a staker j on the other dimension, with the diagonal squares as the rectangles where the user in the two dimensions is the same.

In Miller et al, variations on the Cluster Match are considered that weight some of the off-diagonal rectangles in these types of diagrams less with the goal of making the mechanism resistant to various types of collusion. Specifically, they consider a version of this idea that they call the "Correlation-Oriented Cluster Match" where the subsidy corresponding to the rectangle for users i and j is reduced if there exists some user k that shares at least one SBT with each of users i and j. This turns out to have various good collusion-resistance properties.

More concretely, the Correlation-Oriented Cluster Match might look to see if there were users with both the "HTML expert" SBT as well as "design expert" SBT. Then, if these groups do indeed turn out to overlap, the system sees these SBTs as perhaps not truly representing two different groups and reduces the matching funds it gives accordingly. In fact, even if there are no users that have both the "HTML expert" SBT and the "design expert" SBT, but there are some jurors from each of these groups that share a common third "Javascript expert" SBT, then the Correlation-Oriented Cluster Match views the "HTML expert" and "design expert" groups as having some underlying connections and discounts its matching funding accordingly.

One might ask if these ideas of re-weighting certain regions of these square diagrams could be useful when using SBTs to determine jurors' odds of being drawn in Kleros. Attack resistance is slightly different in the application of Kleros juror drawing version in quadratic funding. A manipulation that allows an attacker coalition to increase the sizes of the squares might be okay if it does not affect the relative size of the honest square to the attacker's square. Hence, the exact re-weighting formulas that make sense for Kleros might be different from those that make sense for quadratic funding. Finding such improved versions of mechanism (SBT-CM) is an active subject of research.

Nonetheless, as the line of ideas seems to apply to both quadratic funding schemes and the token-weighted random draws used in Kleros juror selection, one might ask if there is some general family of mechanisms which one can SBT-ify in this way. Are there other similar applications where it makes sense to take a similar approach?

Resistance of (SBT-CM) to whale attacks

How does the resistance of (SBT-CM) to whale attacks compare to that of the other mechanisms we have considered?

Note that, if i is an attacker, the side length of her square in the diagrams above is:

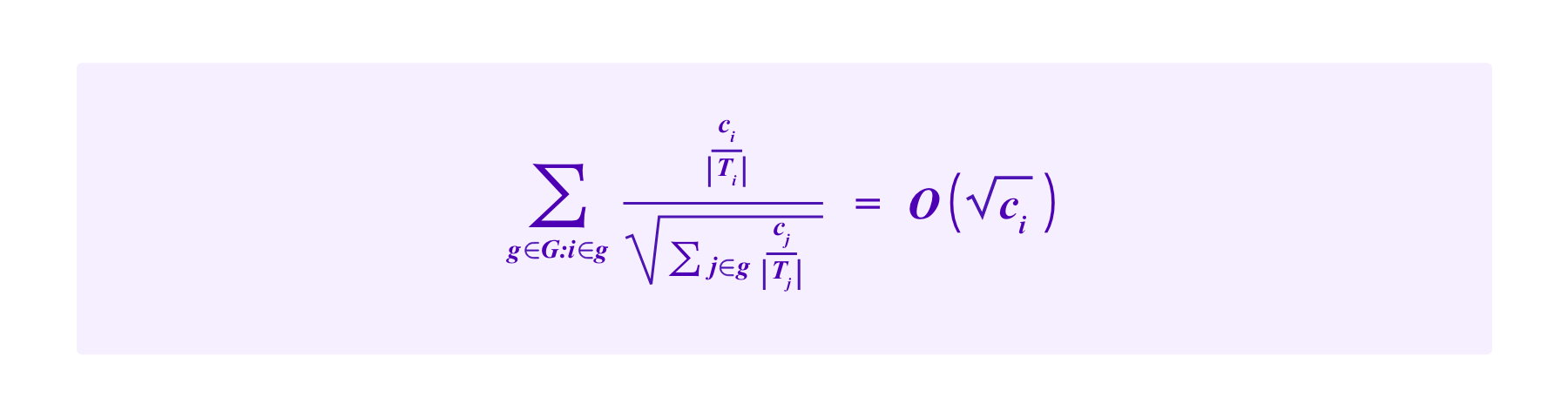
Suppose that the attacker is incapable of obtaining SBTs that do not actually correspond to her identity. Then, by increasing her stake, the attacker can influence the size of the honest square only insofar in that if she shares SBTs with some of the honest participants she can decrease their weight. The weight of elements of the honest square corresponding to SBTs that the attacker does not have are unaffected.

Let a be the side length of the attacker's square, and let h be the side length of the square of stakes of honest participants that do not share SBTs with the attacker. Then, the attacker's chances of being drawn are bounded by:

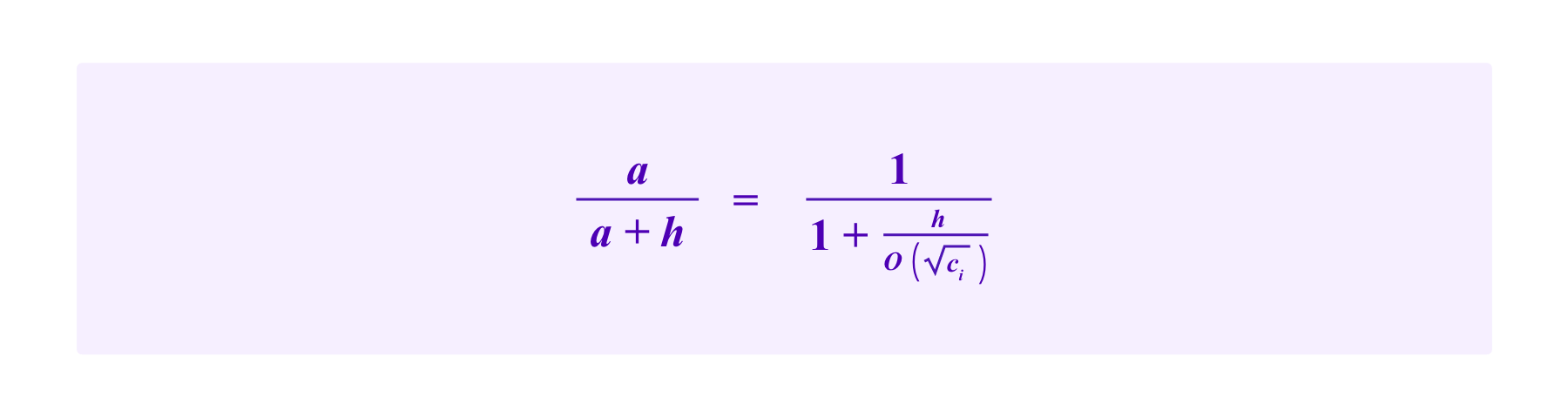
Then, as the attacker increases her stake, each additional PNK gives her proportionally less weight in being drawn due to this quadratic effect. Essentially, the more the attacker stakes, the more this mechanism sees the attacker's SBTs as being common and not being a priority for selection. Thus, it generally is more difficult for an attacker to obtain drawing chances higher than 50% than in mechanism (T).

On the other hand, suppose we have an extreme situation where there is only a single SBT that can be held by honest users, but that an attacker has managed to construct k malicious SBTs that only she possesses.

For example, imagine that the process that awards "design expert" SBTs is secure, but the attacker has corrupted the private key of the online academy that awards "HTML expert" and "Javascript expert" SBTs. In this case, the attacker has managed to corrupt k=2 SBTs. How much of an edge can such an attacker get in her chances of being drawn?

Moreover, suppose that the attacker can attribute the malicious SBTs at will to Sybil addresses so that she can allocate her stake at will between the different groups and does not have to follow weighting scheme that (SBT-CM) imposes on honest users of allocating ci/|Ti| of a total stake ci to each of |Ti| groups.

Denote H to be the total stake of the honest users and A to be the total stake of the attacker. In this scenario, one cannot hope that the system is resistant to the attacker also controlling the majority of the stake, so we assume that H>A.

Then if the attacker stakes c1,...,ck on addresses that each hold one of the malicious SBTs and she stakes

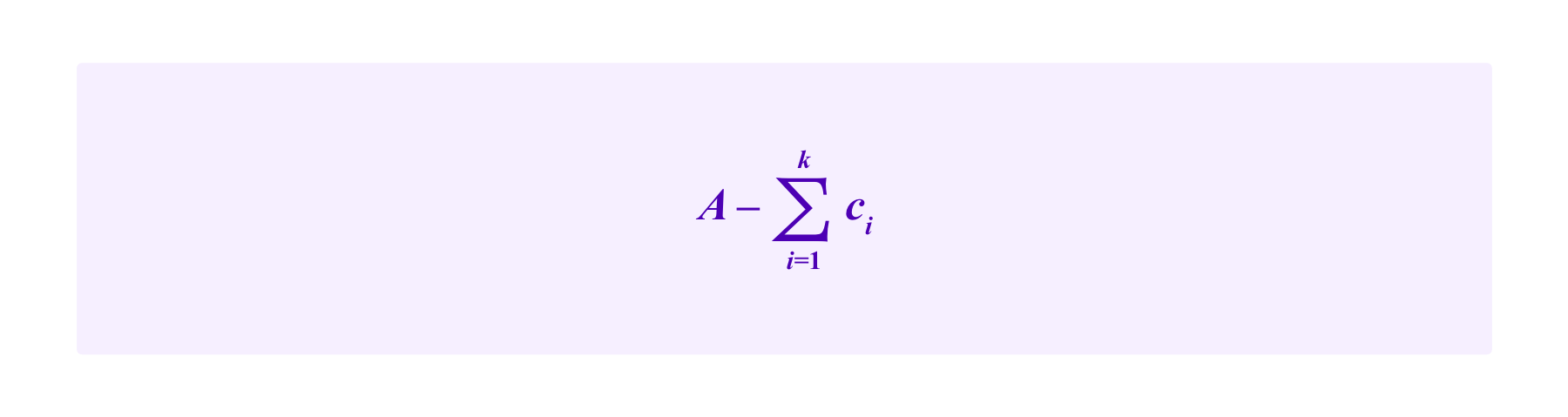
on an address that holds the honest SBT. Then the attacker's chance of being drawn is at least 50% on any given draw (and hence the attacker can expect with high probability to obtain the majority of the votes in a case with high probability by the law of large numbers) if and only if 

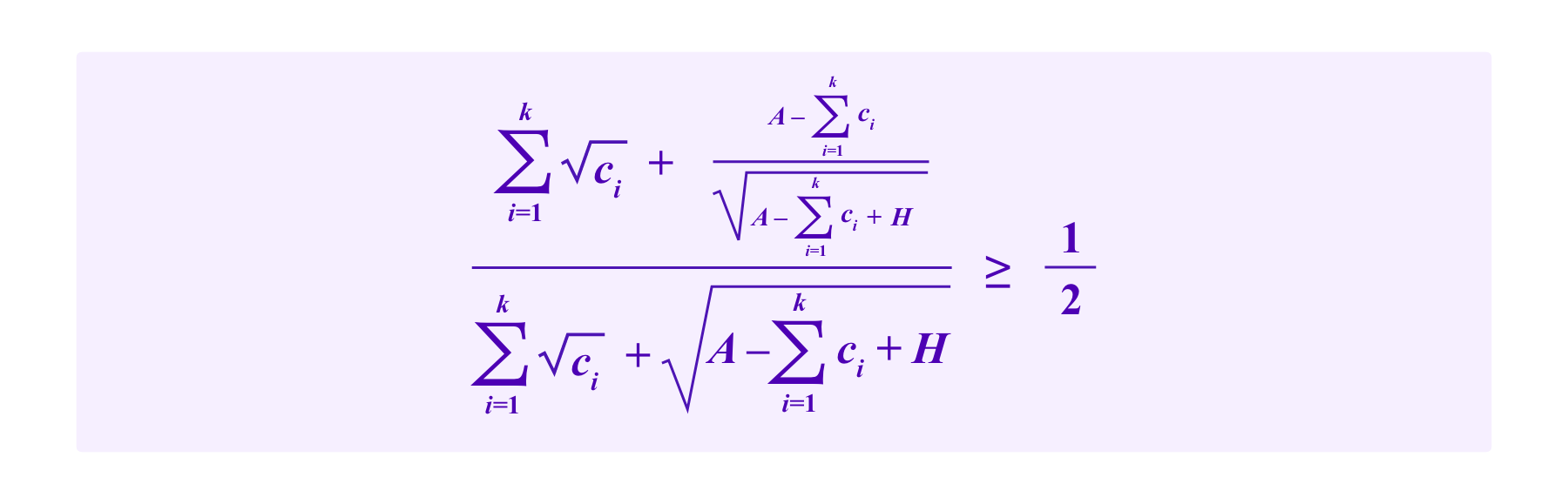
A straightforward optimization argument shows that the attacker maximizes her chances by splitting the stake she puts on the addresses with the malicious SBTs evenly between the those k addresses. So then if the attacker stakes c with each of the addresses with the malicious SBTs, the system is vulnerable to the attack if and only if

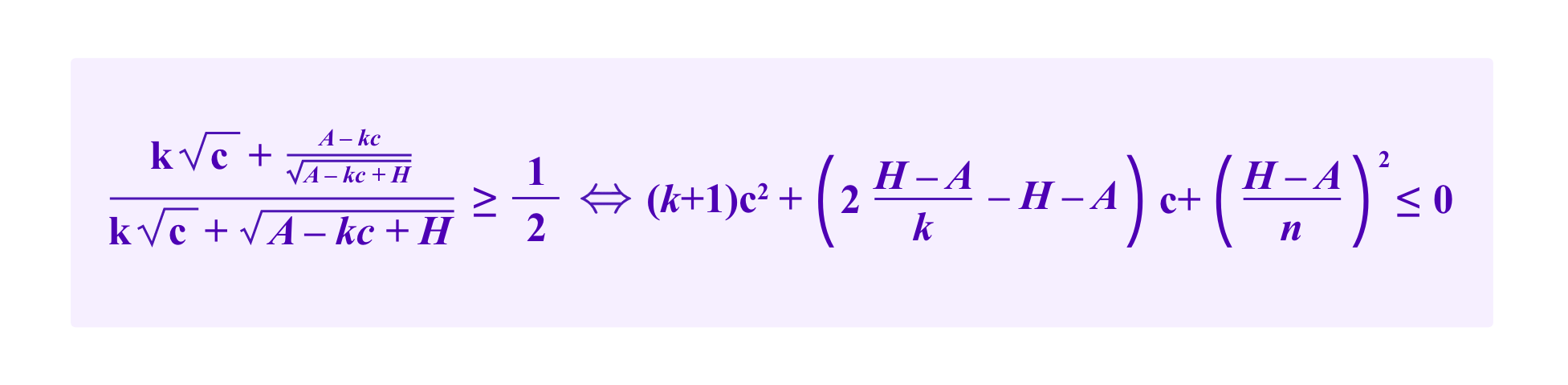
Noting that c can take values in [0,A/k], the quadratic on the left-hand side is minimized either at an endpoint or when

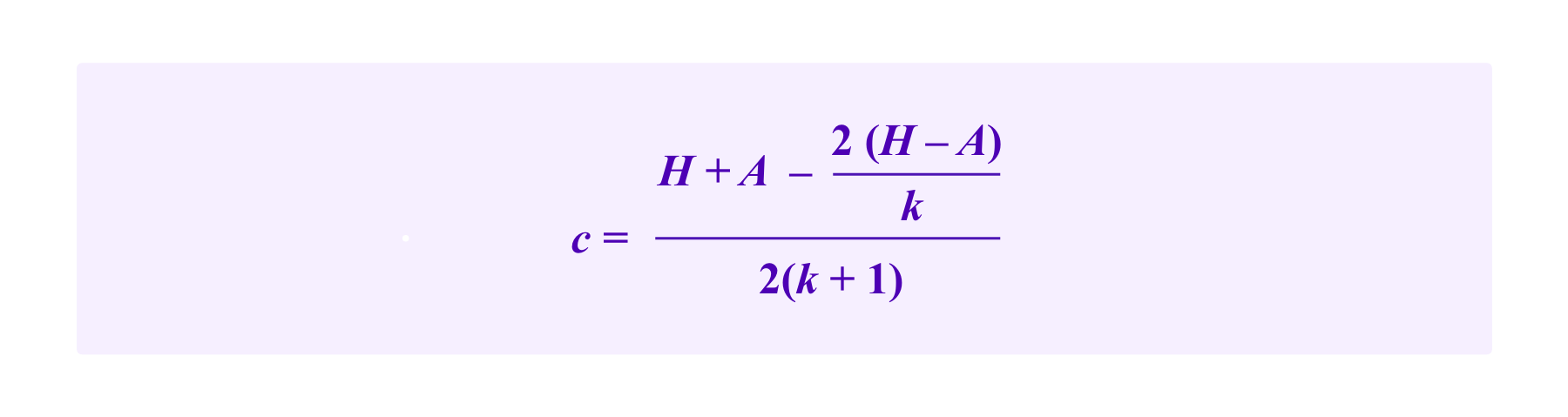
One notes that the critical point falls outside the interval [0,A/k] if

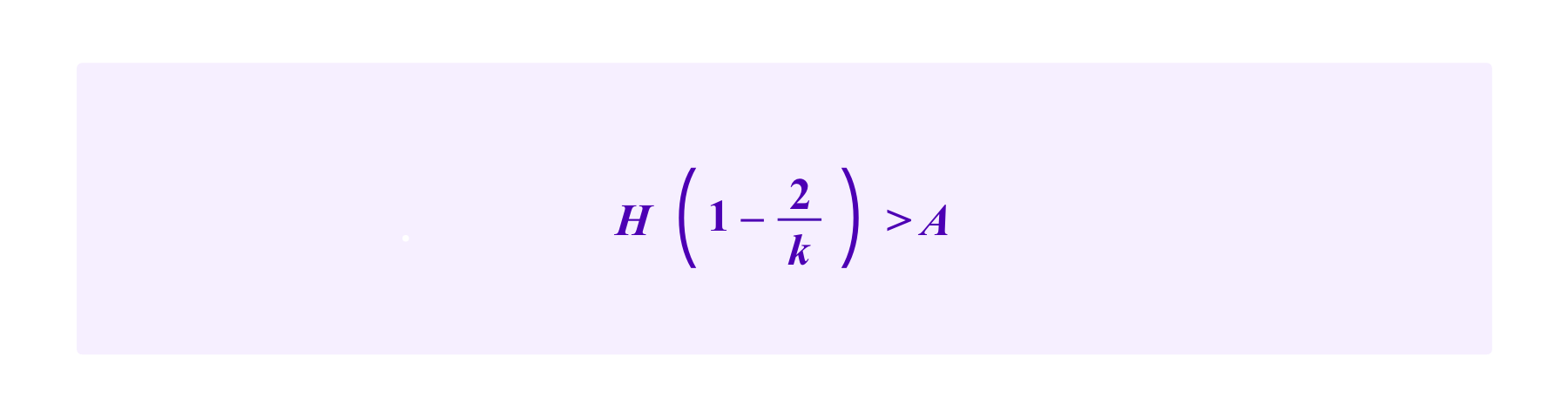
In this case, the attacker maximizes her chance by assigning A/k tokens to each of the k addresses with a malicious SBT and no stake to the address that possesses the honest SBT. Then the attacker would have at least a 50% chance of being drawn on any given draw if and only if

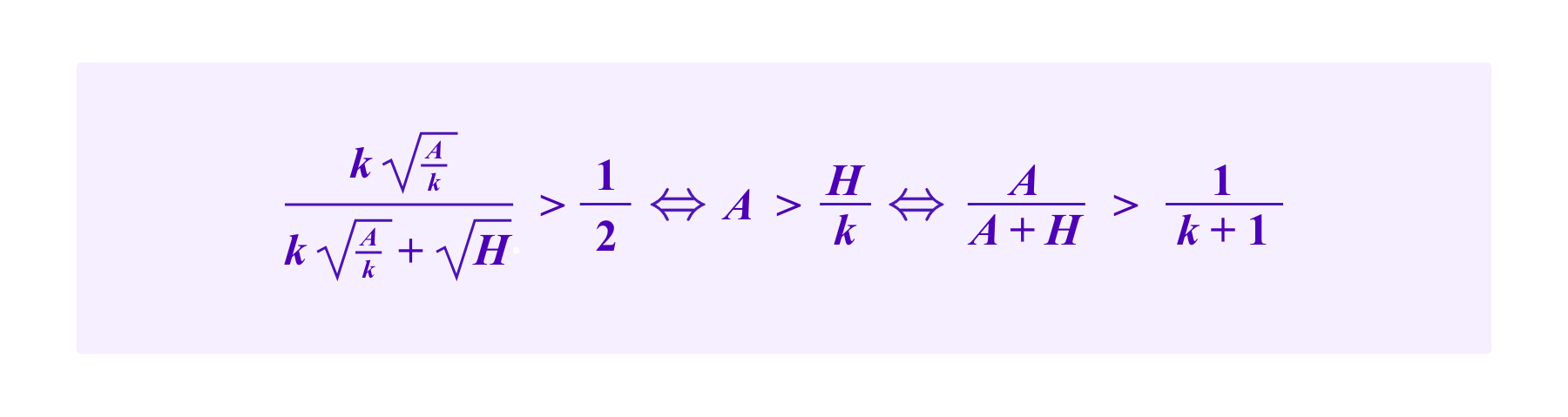
So for an attacker to successfully attack this system with a proportion of the stake of less than 1/(k+1), namely with A<=H/k, the critical point c must fall in the interval [o,A/k]. Then,

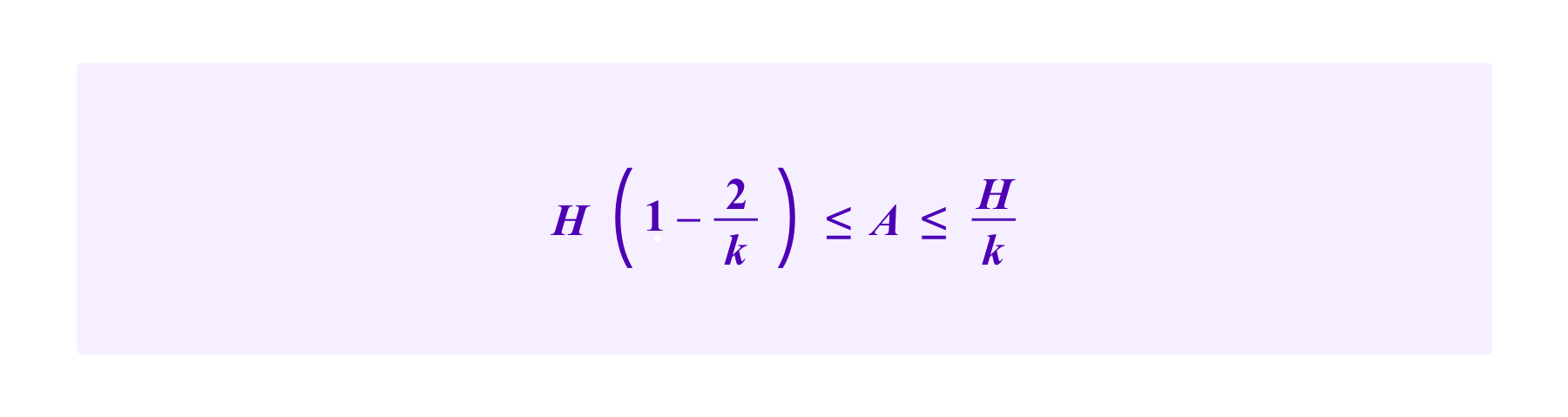
which, is only possible for k<=3.

For k=1,2, and 3, one can plug the critical point above into the above inequalities and solve for a threshold of A/H at which there does not exist a choice of c where the attacker obtains a chance of 50% of being drawn or greater. In this way, we see that the thresholds at which a whale attacker has a large enough stake to launch a successful attack are the following:

So, while one might want to avoid having a mechanism that takes into account many SBTs in a single draw, a system that considers moderate number of SBTs still requires a large attacker stake to break even if the attacker manages to corrupt the allocation several of the SBTs.

Note that one could also naturally combine this approach with mechanism (H) forcing users to have all of their SBTs on a single wallet tied to their Proof-of-Humanity profile in order for them to be considered in the user's drawing chances. Then, one can do an analysis to see that an attacker that can both 1) obtain malicious PoH profiles AND 2) corrupt the distribution of one or more SBTs would still need a substantial stake in the court. Thus, the SBT-weighting can be thought of as again complementing the other mechanisms to provide a multi-layered resistance against whale attacks.

Other goals for a juror drawing formula using SBTs

One might ask what other properties one would want from such a drawing formula. One natural goal is the following:

• i's chances of being draw should be monotonically non-decreasing in the amount of PNK that i stakes.

This is related to the concept of “individual rationality” discussed in Miller et al where one does not want a project in a quadratic funding scheme to receive less funding because someone makes a contribution to it. In the case of Kleros, one would want to make sure that a whale attacker has to take on as large of an economic cost as possible. One can show that model (SBT-CM) satisfies this property.

Another property that one might want could be:

• Have a built-in notion of which SBTs are “positive” and which are “negative” (for example, by having curated lists of such SBTs arbitrated by Kleros). Then, if a juror obtains a “positive” SBT this should not decrease her chances of being drawn.

The (SBT-CM) model does not satisfy this property. Indeed, even if one thought of all SBTs that are taken into account by the model as being positive, a user i's chance of being drawn will generally decrease if she obtains an additional, common SBT. One might study adaptions of these ideas that try to study adaptions of this model where gaining an SBT that attests to useful expertise is never penalized.

Eigendrawing

One idea that has been evoked in Weyl et al and Miller et al is to potentially improve upon the Cluster Match weighting in quadratic funding schemes is to group contributors with more sophisticated clustering algorithms. Namely, the formula for the amount of funding under the Cluster Match:

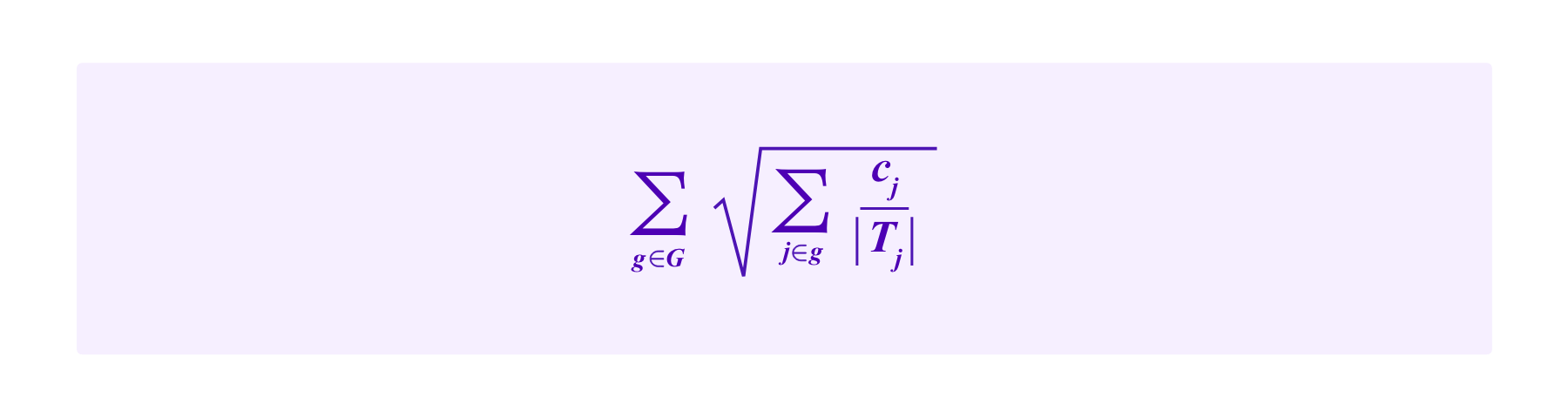
takes a fixed set of groups G to which the contributors belong, such as the group of contributors that hold each given SBT. Then, when a contributor i belongs to more than one group, this approach evenly divides her contribution between the |Ti| groups to which she belongs with ci/|Ti| being attributed to each group.

Instead of considering users as belong to fixed groups like this, one could instead assign them to groups using a clustering algorithm that takes into account which SBTs the users hold to get a sense of the similarity or the difference between the users, but where the algorithm is more flexible in how it uses this information. One possibility for such an approach would be to use spectral clustering.

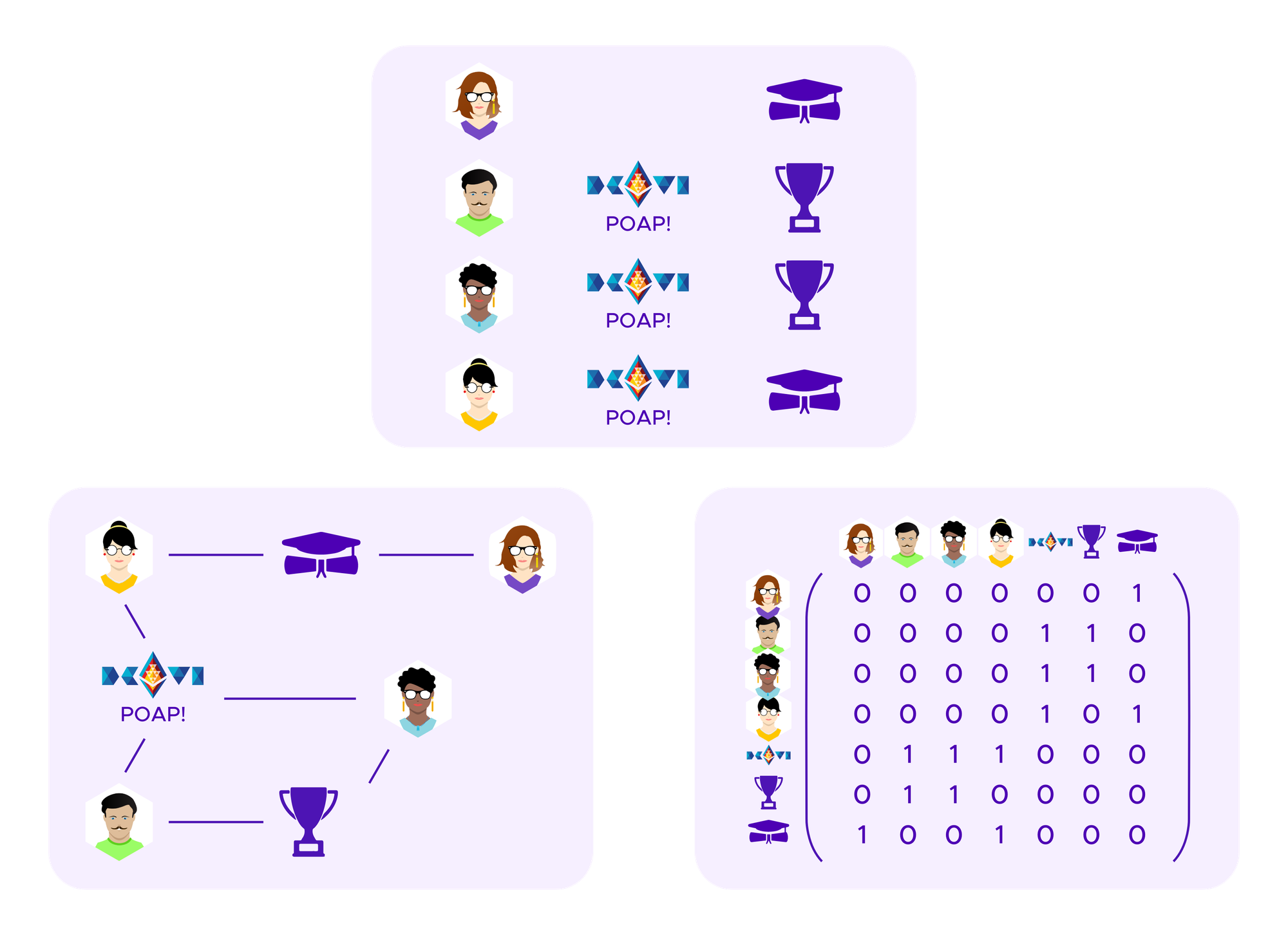
The basic idea of spectral clustering is to form a graph that encodes the information about which users have connections to each other, in this case which users have which SBTs, see above. From this information one can generate a matrix, called the "graph Laplacian" whose eigenvectors turn out to tell interesting information about the clusters in the graph.

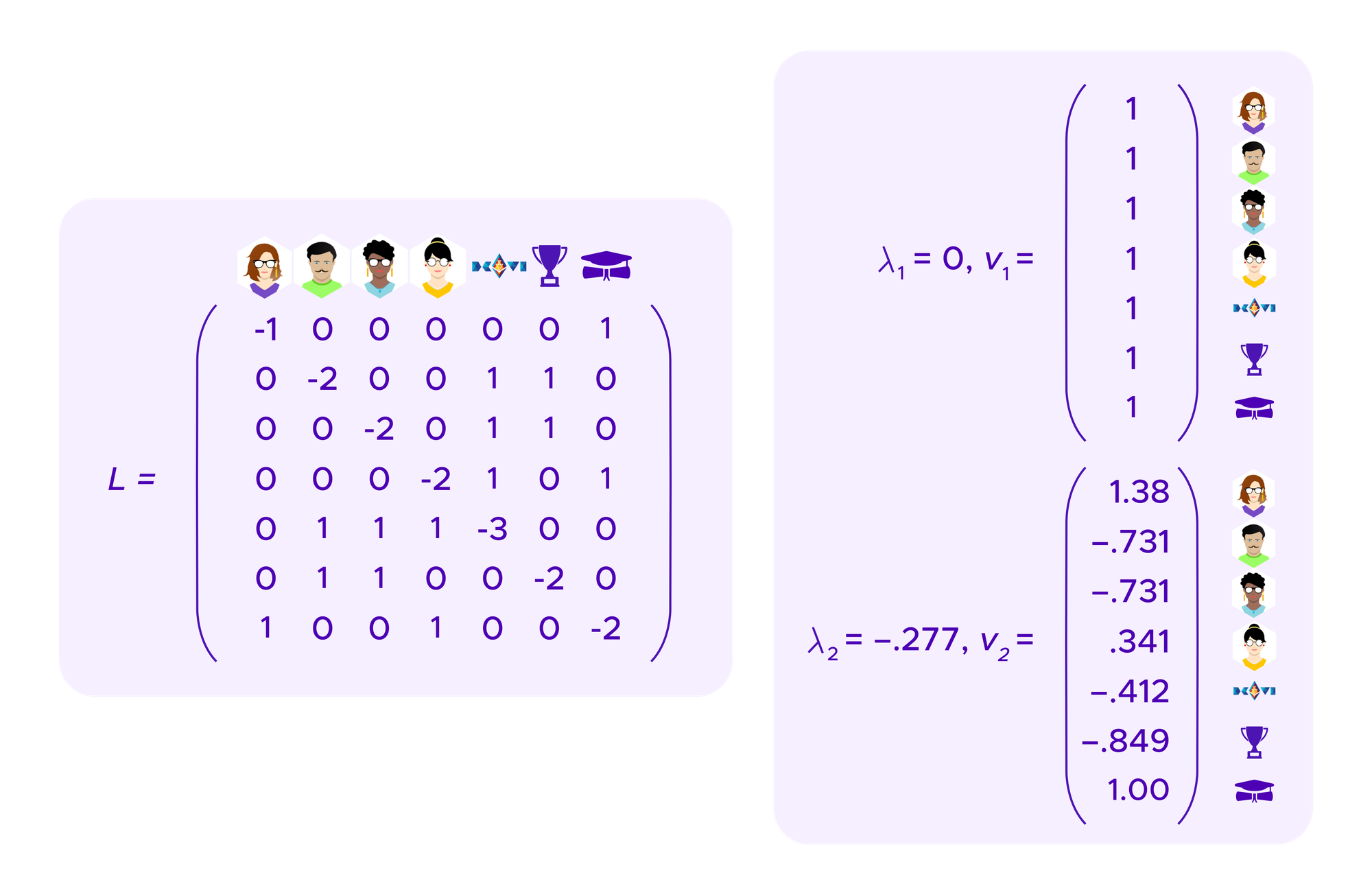
Specifically, if the graph of points that one is trying to cluster consists of k connected components, namely k sets of points where there is a path of edges from any point to another within a component but no paths of edges between the components, then the graph Laplacian has 0 as an eigenvalue with multiplicity k and where one can find k eigenvectors that have coordinates of 1 for points in the cluster and coordinates of 0 for points not in the cluster. Namely, these eigenvectors allow one to read off which points are in which cluster.

One is generally interested in graphs that don't quite split up into distinct connected components, but which "almost" do. One can make arguments using perturbation theory that show that in this case, the eigenvectors of the eigenvalues closest to 0 allow one to recover information about these approximate components, breaking the graph into clusters.

Then, a quadratic funding scheme using these ideas, could be given by projects receiving a total funding amount of:

This is, more or less, what is proposed in Weyl et al and Miller et al as "Eigenmatch".

One possible way to adapt this idea to an even more subtle handling of the graph information given by which users have which SBTs would be to use "soft spectral clustering" techniques which instead of simply assigning each participant to a cluster, give a probability that that participant is in each cluster. Then, one could have, for example, a quadratic funding scheme where projects receive:

Of course, these ideas can then be applied to Kleros juror drawing. One possible, relatively direct way to apply this clustering approach to the SBT-weighted drawing techniques discussed above would be the following mechanism which we call "Eigendrawing".

Model (SBT-ED)

Using the notation above, the participant i has a chance of being drawn of:

How this formula interacts with the various attack resistance questions discussed above is still an area of active research.

Conclusion

We have considered a variety of possible ways that jurors in a system such as Kleros can be drawn. All of these techniques have been enabled by the creation of new blockchain identity tools that did not exist when Kleros 1.0 was launched. Nonetheless, one is prevented from using many of the existing reputation schemes that one might find in a web2 crowdsourcing platform as

• the blockchain-based identity tools, while improved, still may not capture the full scope of identity information that a web2 company may be able to obtain on its users, and
• the extremely hostile environment of blockchains requires one to design mechanisms around very conservative attack models, notably compared to web2 systems where a central authority may have the ability to punish misbehaviour that it observes in an ad-hoc fashion that does not have to be built into the model in advance.

Thus, we have focused on the attack resistance of these different drawing mechanisms. We have seen that it is possible to build drawing mechanisms using these new blockchain-identity tools where different types of attack resistance to whale attacks complement each other. In order to break such a system, it should be necessary to have the large numbers of a token that would be required to break a pure staking system, to be able to obtain many profiles on a Proof-of-Personhood such as Proof-of-Humanity as would be required to break models that choose jurors from among random profiles, AND to corrupt the assignment of Soulbound Tokens.

There are many further research questions that one can pursue in this field to understand exactly how such attack resistance guarantees and other desirable properties of such systems interact. A few examples that could be of interest to researchers in this space are the following:

• Can one improve on the various upper and lower bounds and other approximations made in the above arguments to show sharper bounds on the resistance of these different drawing models to whale attacks?
• How might one adapt the arguments in Miller et al around weighting different regions of the squares representing funding from quadratic funding schemes to the situation described above? Namely, considering that attack resistance against colluding attackers means that the attackers should not be able to increase of the size of the square too much while attack resistance in models such as SBT-CM above means that colluding attackers should not be able to make the "attacker square" too large relative to the "honest square", how can one adapt the ideas from bounds on collusion resistance in the quadratic funding case to the juror drawing case?
• Are there other applications of SBTs where it make sense to apply similar arguments about collusion resistance in terms of such square diagrams?
• How might one build into these mechanisms notions of "positive" and "negative" SBTs, so that users aren't weighted less when as a result of getting a new SBT that attests to some expertise they might have, even if this expertise is fairly common?
• Is the formula in Model SBT-ED above the "right" formula for juror drawing using spectral clustering? What kind of bounds on resistance to whale attacks can one prove under this model?